基于多属性逆向拍卖模型的物流服务交易机制设计＊

汪 磊 王先甲

（武汉大学经济与管理学院系统工程研究所1） 武汉 430072） （贵州大学经济学院2） 贵阳 550025）（武汉科技大学冶金工业过程系统科学湖北省重点实验室3） 武汉 430081）

0 引 言

经济全球化背景下的市场竞争日益激烈.现代企业为增强其核心竞争力，把原本属于内部控制的物流业务外包给专业的第三方物流（third party logistics，TPL），从而专注于核心业务.物流外包是目前企业降低物流成本，分担市场风险，快速响应需求的重要途径.Capgemini［1］的研究表明，西欧、美国以及亚太地区有超过70%的公司选择物流外包模式.2009年我国将物流业列入十大产业振兴规划，单位GDP对社会物流需求系数由2009年的1∶2.8上升至2010年的1∶3.2［2］，物流需求对国民经济拉动进一步增强，物流外包市场日趋成熟.由于物流服务需求的多样性以及服务本身的异质性，除价格外，物流服务需求方对交货时间、经营业绩、物流技术、服务质量等其他非价格属性均有相应的要求.传统的物流交易仅凭价格作为惟一衡量标准显然不能满足物流交易市场的现实需求.因此，理论上需要从多维属性（价格属性与非价格属性）角度刻画物流服务交易行为.由于物流供需双方之间的消费偏好不相同，决策目标不一致，彼此信息不对称.而传统多准则决策方法侧重于客观赋权（数据驱动）或者主观赋权（意愿驱动），不能真实反映供需双方的上述交易信息.因而存在较大的缺陷性.

拍卖作为一种有效的资源配置方式和重要的价格发现机制，通过竞争方式产生拍品（或服务）的价格，并将拍品（或服务）分配给最需要它的单位或个体，从而实现资源的有效配置.传统的拍卖理论研究以标准拍卖模型为起点，价格是其唯一属性，拍卖对象是事先确定的物品（或服务），拍卖只是实现价格发现的过程，而现实中的招投标方式，不是仅凭价格属性的交易活动，还需考虑质量等其他维度的信息.Che最早研究了由价格和质量构成的成本独立的二维属性逆向拍卖模型，构建了“第一高得分”、“第二高得分”、“第二优先投标”三种拍卖协议，并给出了此三种协议下对应的均衡策略，通过采购方设计的评分规则来进行评标［3］.Broanco设计了当成本类型相关时最大化社会福利的两阶段招标模型：第一阶段采购方选择企业；第二阶段采购方与中标企业就质量问题进行讨价还价［4］.Bichler对多属性拍卖进行了计算机仿真实验，研究结果表明多属性拍卖中得到的效用值明显高于传统的单属性拍卖［5］.本文综合应用 Che和 David［6］的拍卖模型，构建了一个多维属性的逆向拍卖模型，并将其引入物流服务交易中，给出了多维属性第一评分拍卖规则，分析了该规则下参与竞标的物流公司竞价策略以及物流服务需求方的期望效用.

1 问题描述及符号说明

假设物流公司i完成属性为qi的任务所需成本为ci（qi，θi）.其中：θi为物流公司i的成本类型，属于私人信息，物流发包方及其他竞标企业仅知道成本类型的概率分布.假设＜＜＋∞）上服从连续可微的F（·）分布，概率密度为fi（·）≥0，令θ＝（θi，θ－i），θ－i＝ （θ1，…，θi－1，θi＋1，…，θn）.假设各属性对物流公司成本的影响是线性且独立的，则物流公司i完成一项属性为qi的 任 务 所 需 要 的 成 本 为Ci（qi，θi）＝式中：cij（·）（j＝1，2，…，m）为物流公司i对单个属性维j的生产成本，它满足（·）＞0，（·）＞0，cij（0）＝0；aij（aij＞0）为各属性的系数因子，表示物流公司i对属性j改进一个单位所需要的成本占整个成本的比重.

2 多属性逆向拍卖模型

2.1 假设条件

模型的合理性必须以假设条件为前提.为研究问题的方便以及保证解的存在性，给出下列假设条件.

假设1V（qi）关于qi是递增的和凹的，且V（0）＝0.即单位质量提高产生的边际价值是递减的.

假设2Ci（qi，θi）（i＝1，2，…，n）关于qi是递增的和凸的，Ci（0，θi）＝0，并且

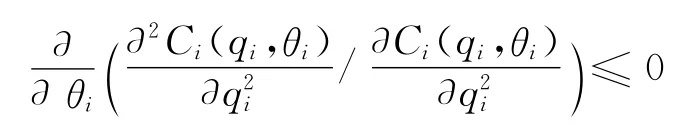
该假设表明，成本类型越低的物流公司提高单位质量所消耗的边际成本越少.

假设3Ci（qi，θi）关于类型θi是递减的和凸的，即

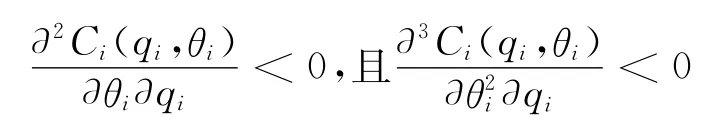
综合考虑假设2和假设3，使得成本函数满足单交叉条件

表流人工湿地的水面位于人工湿地基质以上，其水深多为0.20～0.40m。基于此种人工湿地，污水以较为缓慢的流速进入人工湿地的表层，并存在部分蒸发，部分渗入湿地的可能，但大部分会经出水溢流堰流出。

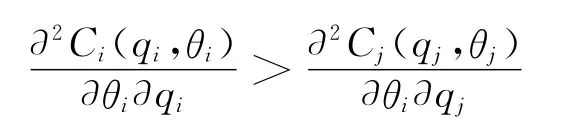
即物流公司i的类型对自己边际成本的影响比对其他物流公司j（j≠i）边际成本的影响更大.

假设4物流公司的类型分布满足单调风险率性质

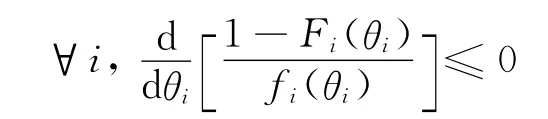
2.2 多属性逆向拍卖模型

2.2.1 物流供需双方的效用函数 根据上述的问题描述和假设条件，参与竞标的物流公司i的成本函数为

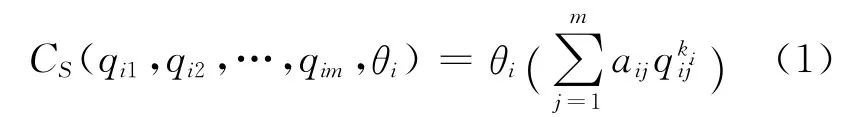
若0＜ki＜1，表明成本函数满足边际成本递减，若ki≥1，表明成本函数满足边际成本递增.基于成本函数，物流公司i的效用函数可以表示为

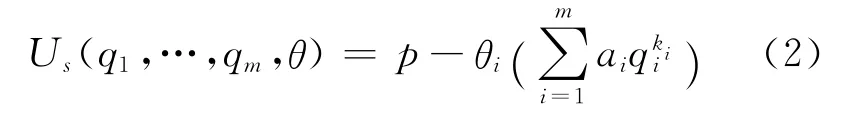
则物流服务需求方的效用函数为［8］

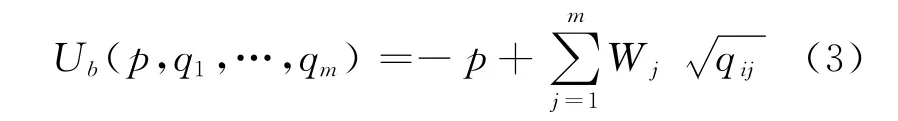
评分函数与物流服务需求方的效用函数结构相同，是确定物流公司赢标的评价标准

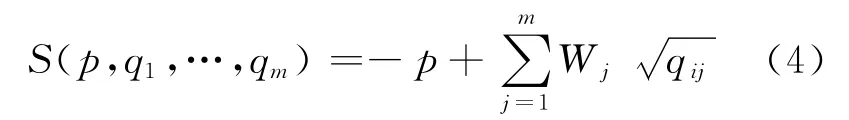
2.2.2 物流公司的投标策略

首先给出引理1，通过该引理确定竞标者的最优质量投标（θ）＝（，…，）.

引理1给定评分规则和投标者的效用函数，在多属性拍卖中使得投标者效用最大化的最优质量属性为qi，qi的选取独立于价格和其他投标者的信念.对θ∈［θ，］的（θ），满足下式：（θ）＝arg max｛V（q1，…，qm）－CS（q1，…，qm，θ）｝，该引理的证明可参考文献［6］.

由引理1求解最优非价格报价（θ），令

由一阶条件可知

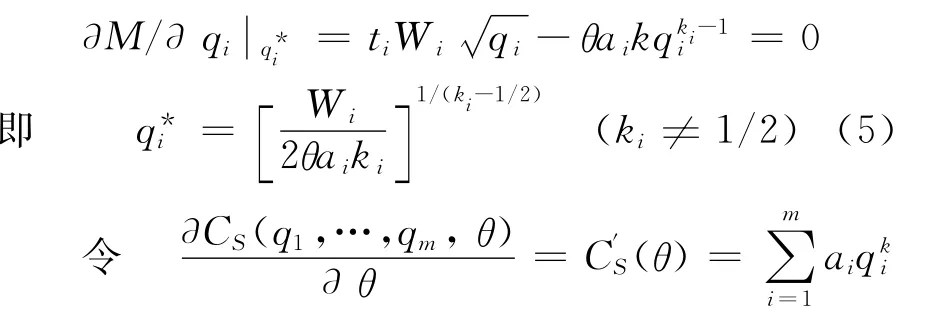
根据Che的模型，有

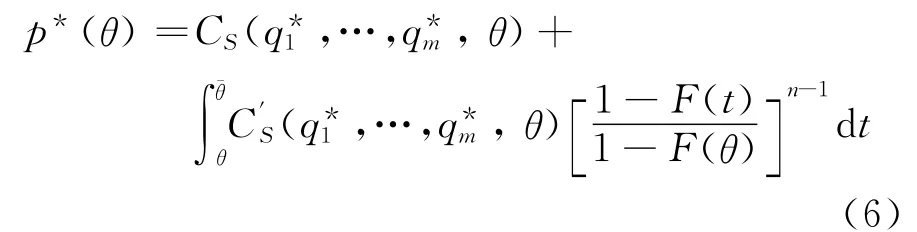
假设成本类型θi服从［θ］的分布，即

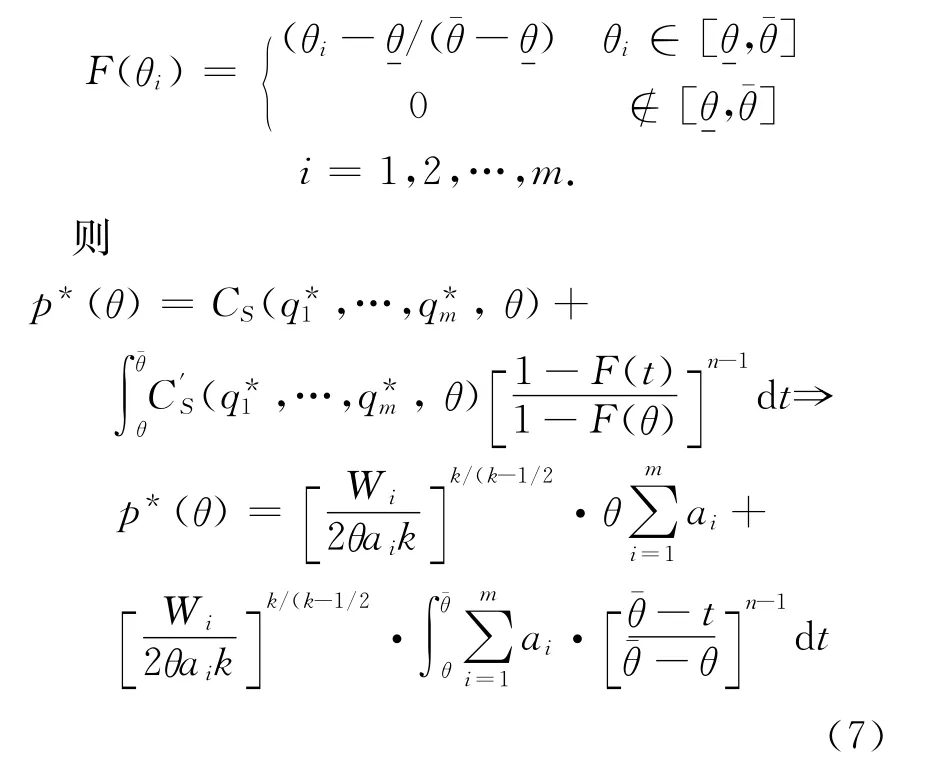
故在第一评分多属性逆向拍卖中，赢标的物流公司提交的报价（p＊（θ），q＊（θ））分别由式（5）与式（7）确定.

3 第一高分逆向拍卖中的物流发包方的期望效用

由于物流发包方具有选择物流公司的决策权，设计该交易机制的目的是最大化物流发包方的期望效用.本文采用Che的多属性拍卖模型中的第一评分规则.由Laffont ＆Tirole的引理可知，成本类型θ最小的物流公司中标.

物流发包方的期望效用计算公式：

由式（8）可知，对于成本类型为θ的物流公司而言，其赢标带给物流发包方的效用为

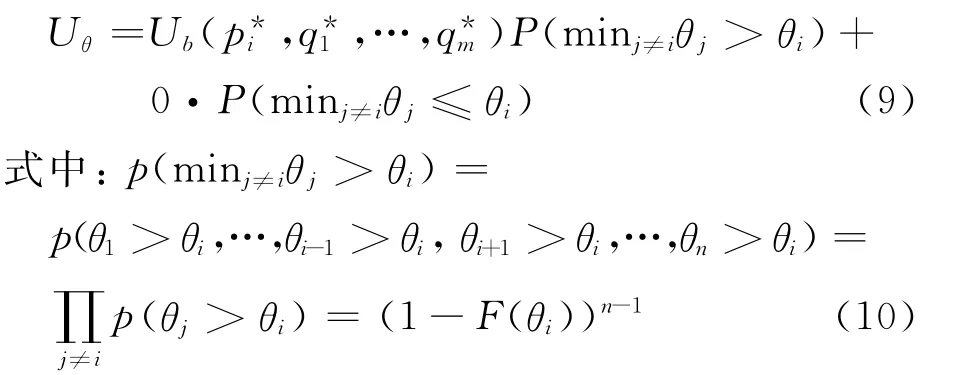
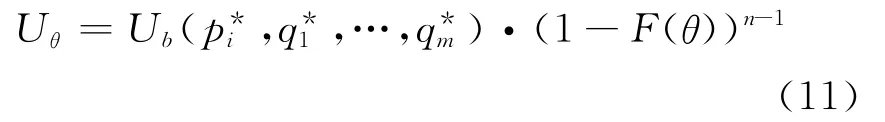
假定θi服从］上的独立同分布.将式（10）代入式（9），可得由于Uθ是属于事前估计的随机变量，对应的概率密度为f（θ），每一个物流投标者都可能成为类型θ而胜出，共有n个投标者，因此，物流外包方的总期望效用为

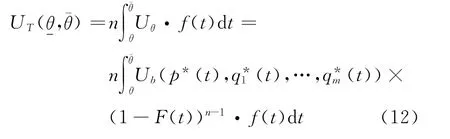
4 结束语

将多属性逆向拍卖机制引入物流服务交易模式中，扩展了物流服务投标者的成本函数，分析了其均衡策略，最后推导了物流服务外包方的期望效用.

考察物流公司的地域性可知，实际中的物流服务投标者包括过境物流公司和本地物流公司两类，显然过境物流公司的成本要低于本地物流公司，说明投标者之间是非对称的，因此，理论中假定投标者之间的对称性不符合现实情况，需要进一步改进.同时运用该多属性逆向拍卖模型描述和刻画现实中的物流交易行为，通过定量分析检验该方法的可行性也是本文今后下一步研究的重点.

［1］Capgemini，Gary R A，Langley C J.Third－party logistics study results and findings［C］／／2004Ninth Annual Study，U.S.LLC：2004.

［2］国家发改委.“十一五”我国物流业取得长足发展［EB／OL］.［2011－10－20］.http：／／www.sdpc.gov.cn／zjgx／t20110119＿391548.htm.

［3］Che Y K.Design competition through multidimensional auctions［J］.Journal of Economics ，1993，24（4）：668－680.

［4］Branco F.The design of multidimensional auctions［J］.Rand Journal of Economics，1997，28（8）：63－81.

［5］Bichler M.An experimental analysis of multi－attribute auctions［J］.Decision Support Systems，2000，29：249－268.

［6］David E.Biding in sealed－bid and English multi－attribute auction［J］.Decision Support Systems，2006，42：527－556.

［7］Laffont，Tirole.Using cost observationto regulate firms［J］.Journal of Political Economy ，1986（94）：614－641.

［8］柳 鹏，刘 清.基于古诺博弈模型的航运物流利润增长效应分析［J］.武汉理工大学学报：交通科学与工程版，2010，34（5）：957－961.