基于航运周期的班轮航线运力配置优化＊

靳志宏 李 娜 陈 梦

（大连海事大学交通运输管理学院 大连 116026）

0 引 言

全球经济危机使国际贸易受到重创，很多船公司吸纳不到足够的货物，市场上运力过剩，加上航运业的退出机制比较缓慢，全球航运企业无不面临严峻的考验.在这种形势下，如何将不同的船舶配置到不同的班轮航线上，对提高船队运输经济效益和整体结构优化尤为重要.介于此，本文根据航运周期内不同阶段的市场运力需求情况将航运周期划分为上行期和下行期.航运上行期市场景气，运量需求大于运力，运价上仰，班轮公司为获取更多利润，巩固并扩大自己的市场份额，可以向其他船东租进船舶来营运.下行期，船公司可以将一部分船舶闲置，合理的进行封存，避免更大的损失.本文研究的即是处于航运上行期的多航线多船型配船与租船的联合优化问题；以及处于航运下行期的多船型多航线配船与运力闲置的联合优化问题.

学术界对航线配船问题进行了多方研究并提出了多种解决方法.谢新连［1］基于线性规划方法对给定的船队和运输任务求解年度最优航线配船.杨华龙等［2］建立了以船公司总净收益为目标函数的线性规划模型.李智等［3］利用神经网络算法求解班轮航线配船问题并进行了仿真计算.赵刚［4］在此基础上，改进了班轮航线配船模型，并给出了新模型的求解方法及收敛性证明.苏绍娟等［5］提出了改进的粒子群优化算法.金雁等［6］将航线配船问题转化为类似的旅行商问题，用蚁群算法求解.Bronmo等［7］构造了一个航线配船主问题和一个基于此主问题的子问题.

上述文献中设计的航线配船问题均仅考虑单程运输，且定义在整个航运周期的上行期，均未考虑往返双向的货运需求，也未考虑航运周期处于下行期的决策环境的变化.本文针对航运的周期性特征，研究了处于整个航运周期上行期的多航线多船型配船与租船的联合优化问题、以及处于航运周期下行期的多航线多船型配船与运力闲置的联合优化问题，且同时考虑了往返双向的货运需求.

1 建模条件与符号说明

本文假设以期租的方式租船，待配置船舶的营运性能、技术性能、航线的货运任务、以及港口条件等都是相适应的，每艘集装箱船舶在两港之间往返运输，不考虑中途挂靠港口或加载集装箱等因素.

文中的符号定义如下：

航线集合C＝｛j｜j＝1，2，…，n｝；公司现有的船舶种类集合V＝｛i｜i＝1，2，…，m｝；租船市场可供租用的船舶类型集合V′＝｛i｜i＝m＋1，m＋2，…，m＋z｝，即第m＋1至m＋z型船为可租用船舶类型；第i种船舶的数量是Si；Wi是第i种船型的装载量；参数tij是一艘i型船在第j条航线上一年可完成的最大往返航次数；Kij为一艘i型船舶在第j条航线上完成一个往返航次所花费的成本；T为规划期；L为船公司规划期内的利润；Ri为i型船在规划期内的期租租金；Ii为i型船在规划期内的闲置费用；Fi为是每艘i型船在规划期内的固定成本；Qj1和Qj2分别是第j条航线上规划期内正、反向货运量预测值（TEU）；Pj1和Pj2分别为第j条航线上正、反两向每单位运量（TEU）的运费收入，即运费率.

决策变量xij为分配到第j条航线上的i型船的艘数；zi为i型船的闲置数量.

2 上、下行航运周期的运力配置优化模型

2.1 上行期航线配船与租船联合优化模型

目标函数：

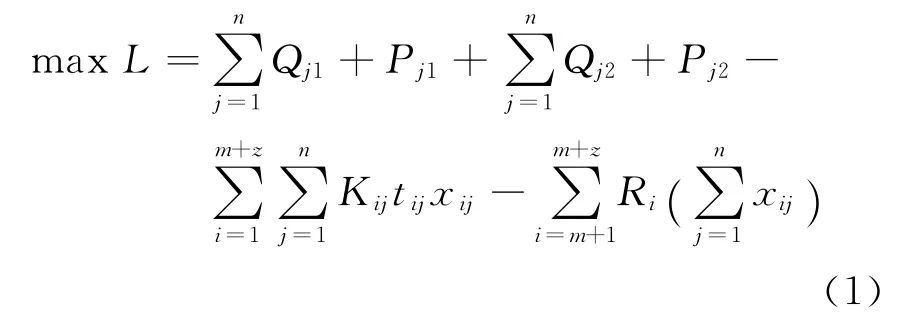
约束条件：

在上行航运周期中，公司现有的船舶均投入运营，如何分配船舶与固定成本无关.期租租进的船舶只需按期支付租金，固定费用已包含在租金内.因此为避免冗余，模型的目标函数（1）不考虑船舶固定成本，只考虑收益与航次成本和租金的差值利润.式（2）～（5）是模型的约束条件，式（2）为船舶数量约束，式（3）和式（4）是运力满足正、反向运量需求.式（5）为变量自身约束.

2.2 下行期航线配船与运力闲置联合优化模型

目标函数：

约束条件：

在下行期，船舶封存后，固定成本中的营运成本节约了，但发生了诸如港口费、保养费用、看船人员工资等相关成本，在本文统一纳入闲置费用Ii.因此下行期的目标函数式（6）需要考虑固定成本和闲置成本.式（7）～（10）对应于（2）～（5），作为相应的下行期约束条件.

3 模拟退火算法求解

航线配船混合整数规划模型是一个典型的组合优化问题，也是一个NP－hard问题.鉴于此，本文设计了模拟退火算法以求解现实规模问题.

3.1 算法中的若干技术问题

算法中符号定义如下：LL为模拟退火算法目标函数；X为模型的解；T为系统的温度；ΔL为两个目标函数的差值；M为充分大的数；δ为任取两个解的目标函数值之差；lk为模拟退火算法第k次迭代时马尔科夫链的长度；v为算法中的迭代步长.

航线配船问题的目标函数为求最大值，将其转化为模拟退火算法的最小值问题：LL＝M－L.

上行期解的表示形式为

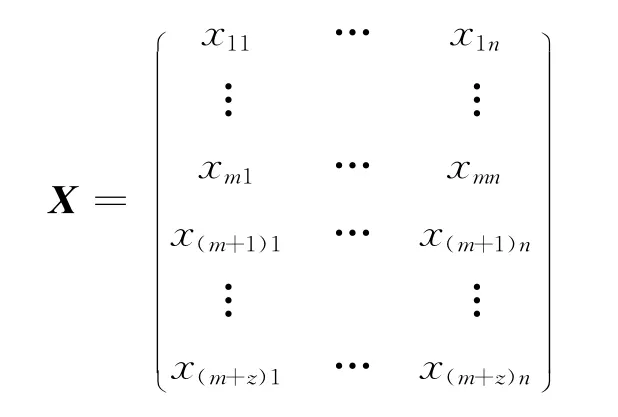
下行期解的表示形式为

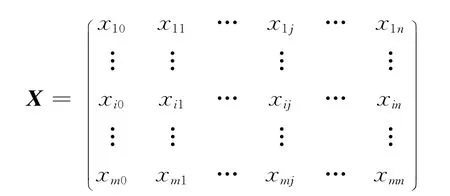
在下行期解的表示中，设置第j＝0条航线为虚拟航线，闲置的船舶分配到这条航线上，即当j＝0时xij表示的意义为：第i型船闲置的数目.

新解的产生机制是在定义域范围内，随机产生一个i和一个j，对应的解分量为x（i，j），然后利用随机产生装置产生一个新解x′（i，j），使x′（i，j）∈［x（i，j）－1，x（i，j）＋1］.针对新解x′（i，j）计算新的目标函数值LL′，如果x′（i，j）满足船舶运力与运量约束条件而且LL′＜LL，则接受新解，若LL′≥LL，则按照概率e（－ΔL／T）接受新解.

初始温度设为T0＝Mδ.设α是一个介于0与1之间的常数，降温规则取Tk＋1＝αTk.设β是系数，则马尔科夫链增长的方式为lk＋1＝βlk.当系统温度小于或等于停止温度Tf时，算法停止.

3.2 算法流程

用模拟退火算法求解模型的流程见图1.

图1 模拟退火算法求解流程图

3.3 参数试验

冷却进度表共有5个参数需要确定，分别为初始温度的参数M、停止温度Tf、温度衰减系数α，以及马尔可夫链长度的初始长度l0和增长系数β.以一个3种船型共20艘船舶6条航线的配船问题为例，针对要试验的参数选取不同的组合值，分别计算目标函数值，图2，3中横坐标分别对应参数的其他4个试验值.参数的选取原则是选择能得到质量最优的参数组合，经过试验发现，在上行期，当M＝20，Tf＝0.1，α＝0.9，β＝1.1，l0＝90时算法可以达到最优；在下行期，当M＝10，Tf＝0.5，α＝0.9，β＝1.15，l0＝90时算法可以达到最优，因此分别将其作为上、下行期航线配船问题的模拟退火算法的参数.

图2 上行期参数试验结果

图3 下行期参数试验结果

4 班轮航线配船联合优化问题算例分析

4.1 小规模问题的算法评价

用模拟退火算法对上述小规模航线配船问题进行求解，与Lingo软件求得的最优解对比，对比结果见表1.

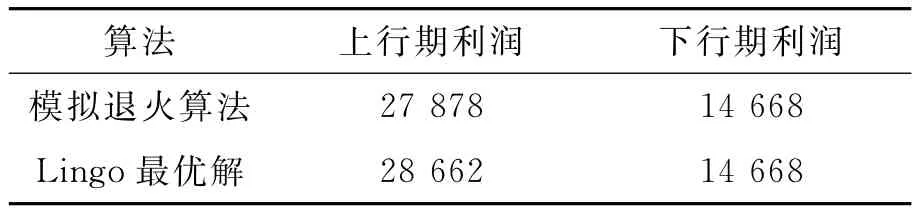
表1 小规模问题与Lingo最优解比较 万美元

从表中结果可见，在上行期，模拟退火算法的解仅比精确解差2.81%，下行期结果完全相同.从处理的时间上看，模拟退火算法耗时更短.显示了本文设计的模拟退火算法能较好的收敛到近似最优解.

4.2 现实规模问题的算法评价

为了进一步考查算法的实用性，以某船公司的现实规模的运力配置问题为例进行仿真实验.该公司拥有6种吨位的集装箱船舶共100艘，分别是1 500TEU的10艘、1 400TEU的15艘、1 000TEU的20艘、850TEU的17艘、800TEU的20艘、500TEU的18艘，现开辟班轮航线10条，市场上有2种类型可供租用的船舶.

用上述混合整数规划模型与模拟退火算法求得航线配船结果见表2～3.表中数据代表某一船型在某一航线配置的数量.上行期目标函数值152 208万美元，下行期目标函数值59 158万美元.

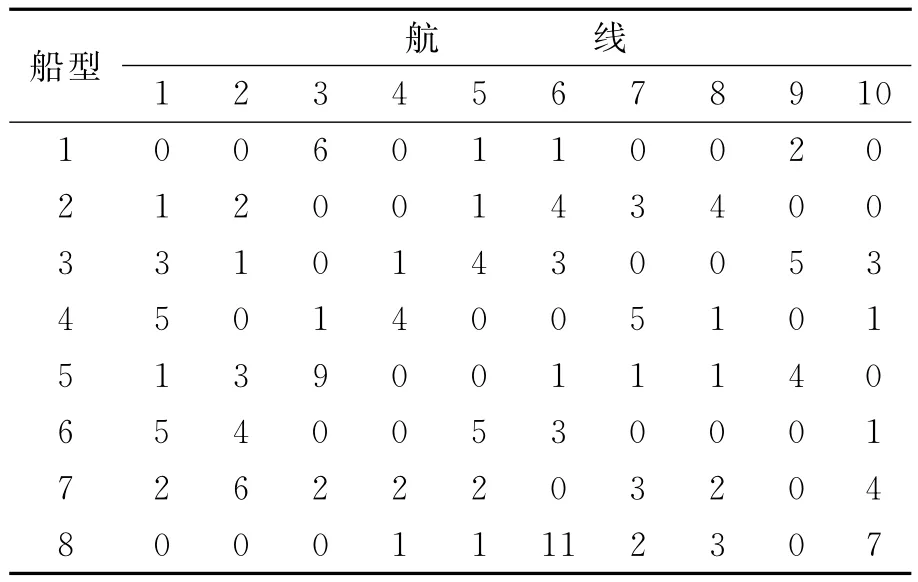
表2 上行航运周期航线配船结果

表3 下行航运周期航线配船结果

5 结束语

本文基于客观存在的航运的周期性特征，分别针对处于航运上行期的多航线多船型配船与租船的联合优化问题、以及处于航运下行期的多航线多船型配船与运力闲置的联合优化问题，构建了混合整数规划模型，基于模型特点开发了相应的模拟退火算法，通过小规模问题实验确定了模型与算法参数，并通过与Lingo最优解的对比，显示了模型及算法的有效性.同时，大规模现实问题的算例分析也进一步验证了算法的实用性，可为集装箱班轮航线运力配置提供决策支持.

进一步的研究将考虑具有中途挂靠港口或者加载集装箱等因素，即船舶在3个及3个以上港口之间往返运输的运力配置优化问题.

［1］谢新连.船队规划的动态模型与算法［J］.中国造船，1992（3）：102－130.

［2］杨华龙，钟 铭.集装箱班轮航线配船优化决策研究［J］.大连海事大学学报，1996，22（3）：51－54.

［3］李 智，陈明昭，董治德.基于神经网络的班轮航线配船优化方法［J］.交通与计算机，2001，18（90）：34－36.

［4］赵 刚.班轮航线配船模型的分析与改进［J］.系统工程学报，1997，12（1）：80－86.

［5］苏绍娟，王丽铮，王呈方.不确定性航线配船数学模型建模方法［J］.航海工程，2007，36（4）：99－103.

［6］金 雁，赵 耀.基于蚁群算法的航线配船［J］.计算机工程与应用，2007，43（25）：231－233.

［7］Brønmo G，Nygreen B，Lysgaard J.Column generation approaches to ship scheduling with flexible cargo sizes［J］.European Journal of Operational Research，2010，200（1）：139－150.