中国（传统）绘画透视的科学验证

乌明韫

（福建农林大学，福建 福州 350002）

1 “龟纹图”透视变化规律

正等轴测图、正二等轴测图、正三轴测图能反向变化为透视图[1]。同样，正等轴测图、正二等轴测图、正三轴测图是透视图反向畸变到极限值时的极限图形[1]。由于正三轴测图在各轴测轴具有各自不同的轴向伸缩系数，轴间角可以选取多种不同的角度，所以对任何一个物体来说，均可以作出无穷多的正三轴测图[2]。图1为透视畸变渐变图，它是“龟纹图[1]”里的一幅图。焦距从50毫米至10000毫米，由于物距加大，透视图(E1F1G1A1D1C1B1)由内依次向外反向畸变。物距的变化使得透视畸变显现出渐变性、连续性和可逆性。A顶点随着透视反向畸变依次变化为A1、A2、……A7、A8；同样，其它顶点由此类推。图中灰色反向畸变图为焦距 270毫米(E5F5G5A5D5C5B5)线框图，其边线A5B5=b5（图2所示）。最外线框(E8F8G8A8D8C8B8)图为轴测透视图（又称：零点透视图、简称：WMY）[3]。

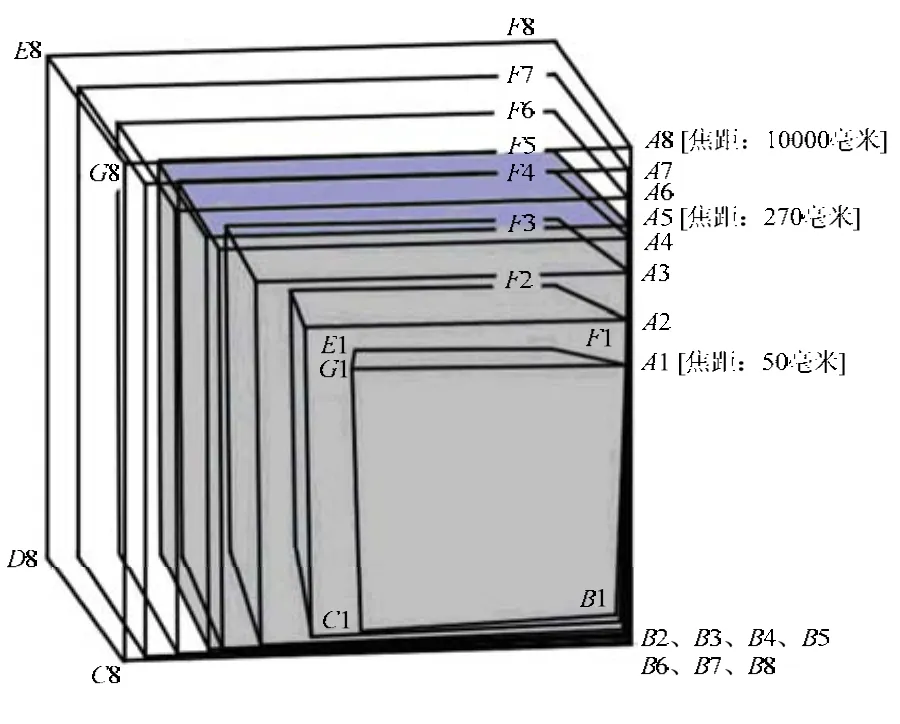
图1 透视畸变渐变图

图2 平移对位图

对于中国传统绘画。总体看来，把透视作为一门学科，他们都未能详细地阐述，且缺乏严谨系统的理论分析和归纳，只是形成了一些绘画模式和法则。这不能不说是一个缺憾[4]。但并没有形成科学系统的理论和科学的验证。中国传统绘画透视已超出裸视，其范围从人眼裸视透视至轴测透视（以下简称：WMY）。“龟纹图”就是透视图与正轴测图的关系变化图[1]，其透视变化规律直接验证了中国传统绘画透视的科学性。该文对 50毫米焦距以上透视效应内容，通过“龟纹图”透视变化规律对中国传统绘画透视中有限物距（视距）透视图至超视距、趋近无限远时，反向畸变极限图形；相对物距、形体与物距相对性进行深入地应用性研究，从而为二维图形图像透视效应提供新的研究路径和技术应用。为中国绘画透视理论提供一个较为完整（整体）的论证。

2 中国传统绘画的透视效应

2.1 山水绘画的透视表现

山水风景在中国绘画中是以透视为基础，而在摄影中则物距与焦距至关重要。同样，在中国绘画中山水其透视效应与摄影（基本）相同。依据“龟纹图”透视变化规律分析，其透视范围从人眼裸视向WMY移动。从意识上，绘画侧重于加大透视的反向畸变[3]。

在这里可设定透视畸变与反向畸变以 50毫米焦距图像为参考值。当物距加大，焦距相应增大时，透视图的反向畸变加大，而物距变化是焦距变化的前题，物距变化是透视畸变的决定因素。换句话说，透视畸变是物距变化的必然结果，焦距是光学镜头反映物像大小的标量。焦距值大小反映出视角范围，同时也表现物像的大小。南宋马远《对月图》、元代马琬《春山清霁图》、明代仇英《松溪论画图》等，以山川美景形式表现。从透视效应上分析，这些绘画的反向畸变透视图视点在中视距与远视距范围内（各幅绘画透视的表现在这个范围内相应视点上）。其摄影表现以50毫米至135毫米焦距段图像为参考值。又如，近代的中国山水画中，李可染《西湖西泠印社》、李行简《秋红时节收获忙》等都表现了中国传统绘画（画师）在透视上的认识和应用。

在这段（物距）透视反向畸变图上，其画面的主要特点是：山川美景居多、占据画面大；建筑等人造元素较少或无，占画幅面积较少，且笔画简要。隋代展子虔《游春图》、南宋马远《踏歌图》、元代马琬《暮云诗意图》、明代仇英《松溪横笛图》、王世昌《山水图》等，则以人与物配合占据趣味点的位置，通过山体、树木、云雾表现透视；近代李可染《清漓胜境图》、张大千《春云晓霭》等，其透视效应与摄影所表现的相似。近代中国绘画在摄影的影响下，画师对透视有更深入的认识，出现物距减小，视角加大的趋势。

2.2 山水和建筑的透视效应

在中国传统透视学（远近法）中，近推远，以大观小；远推近，以小观大。（引自王伯敏、童中寿《中国山水画的透视》）——根据画家当时的审美需要。在取景时，采用类似于望远镜镜头把远处的景物当作近处的景物来处理[5]。南宋刘松年《四景山水图》、明代仇英《江楼远眺图》、清代袁江《蓬莱仙岛图》等。这类画面中需要注意两个因素，即景物的“近大远小”和人为建造物。在中国传统绘画中建筑物的水平线、垂直线和斜线摆放位置明确；水平线和垂直线在视觉上有明显的稳定感，而斜线产生纵深感并具有运动趋势。人的双眼对透视虽能略加校正，但还是有限。近视距仰视庭台楼阁、庙宇、塔楼，在视觉上有不稳定感，表现在（透视）图上也是如此，况且画面表述的内容较少。同样，现代人未受过专业学习和训练看楼房的（倾斜透视）效果图自然不易接受。在西方绘画中这种画面有所表现，如霍加斯《史洛德家族》（1738年）等。由于中国传统绘画受人文文化的影响，在绘画上采用远视距至趋近无限远的俯视透视构图。其建筑物要表现正而稳，又要表述绘画透视中的（内容）全貌。那么，确立垂直线和水平线是中国传统绘画中建筑物稳定感的必要条件，而斜线则是纵深感的立体表现。

2.2.1 水平线

图2是图 1中各反向畸变图边折线E1F1A1B1、E2F 2A2B2、……平移，将F1、F2、……对位至F上。而单个立方体（建筑物）在充满视景框时，图1中焦距270毫米投影图A5B5线（图2，b5）与绘画垂直线相对平行；其（图2）右斜线FA5与水平线向下倾斜45°；左斜线EF与水平线略有向下倾斜约2°。这里需要指出：第一，当视点、物距确定后，形体的透视畸变也就确定。减小焦距以取得较大场景，其透视不改变。焦距值变小，径向等比收缩[1]使形体影像变小，裸视远视距EF线段与水平线段不易区分。观察者视觉误差与徒手绘制误差、随意性都呈现在绘画中。第二，从中国人文观念而言，在视觉上建筑物要有稳当、端正感觉。在不违反透视规律的原则上，以及上述误差允许的范围内，使KF水平线段与EF线段在绘画视觉上重合，以表现中国传统绘画中的水平线段。第三，在工程制图中透视图（效果图）比轴测图作图精度低，且绘画透视表现又比工程透视效果图粗放，中国绘画（透视）又比西方绘画（透视）来的随意。因而在人文、视觉等因素的影响下小角度斜线段EF在中国绘画中视为水平线段绘出。在习惯上水平线比斜线（一定角度）绘制来的简易，尤其对多组线段绘制，因此界画里大量采用。当然，中国传统绘画中也有出现（两斜线）转向较大的三维投影图样的绘画。如：明代谢时臣《武当霁雪图》的紫霄宫、袁尚统《山水》的农舍、清代姚文瀚《四序图》画中的楼台亭阁就是其中透视的典型表现。

2.2.2 垂线、斜线

在三维空间中视点（中轴线移动）、中轴线上视点移动对投影面上斜线角度都产生变化，而在实际空间里要定位视点难度却很大，尤其在远视距俯视条件下。图1，为中轴线上移动视点各物距、焦距值图。从图 1、图2分析：各图 EF边线与水平线的夹角都在∠KFE之内，约2°；在绘画中相当于焦距135毫米图框的A3B3（图2，b3）也可视为与垂直线平行，这与（远）视距、短竖线在视觉误差、手工绘画误差、随意性有关。焦距270毫米以后的b5、b6……竖边线与垂直线相对平行，其物距越大、焦距值越大平行误差越小；由于视点在中轴线上移动，物距加大，∠PFA角度值相应的增加。焦距50毫米∠PFA1为14°、80毫米∠PFA2为25°、135毫米∠PFA3为37°、200毫米∠PFA4为42°、270毫米∠PFA5为45°、500毫米∠PFA6为49°、1000毫米∠PFA7为52°、10 000毫米∠PFA8为55°。调整中轴线拉动视点，则有相应一组数据表现其绘画透视中的斜线变化，焦距为10000毫米时∠PFA8为45°（图略）；多条中轴线上视点的移动（轨迹），有相对应的数据组。因此，从视觉误差、绘画随意性等因素考虑。……在界画中称之为“一去百斜”，其斜度在30°～60°之间[6]。笔者对现有中国传统绘画的影像资料搜集、统计和分析，通过镜向翻转其斜线夹角度数以45°居多，其次为35°、40°。因此，以 45°斜线为参考线。本节以∠PFA5＝45°为参考值。

2.2.3 形体大小与相对物距的关系

“龟纹图”中，透视畸变与物距变化有关。随着物距增加，反向畸变焦距线框图在（X、Y、Z）轴向上，位移变化步幅减小。在（人眼裸视）远视距形体透视畸变受到视觉误差、错视等因素影响难以确定。通常立方体与视点转至相应位置时，如图1所示。往往由于裸视远视距（视点在中轴线上位移）透视的反向畸变微小改变不易被察觉，从视觉上判定为WMY。在中国传统绘画中远景建筑物就是如此表现。然而，从“龟纹图”透视变化规律得知：当视点、视中线不动（目标图标距离不变），立方体等比缩小到一定值时（其相对物距增加，焦距加大），此缩小立方体投影为WMY。因此，当建筑物与视点相对物距加大时，建筑物投影为WMY；反之，视点、视中线不动（目标图标距离仍不变），立方体等比放大为空间体（自然环境），此空间体与视点相对物距变小，焦距减小；目标图标距离和物距都不变时，立方体等比缩小或放大透视畸变变化。那么，表现在画面上周围景物就出现“近大远小”，远景建筑物还是WMY。这里需注意，视点、视中线、目标图标不动，物距相对于形体而言，焦距改变其透视不变。

通过研究简要综述：第一，相对物距增大，形体透视反向畸变加大。第二，在绘画透视中，物距增大到某一值时，建筑物透视反向畸变（视）为WMY。第三，一者，视点和形体目标图标距离一定，视点不动时随着此形体等比放大，其相对物距减小、透视畸变加大；二者，视点不动此形体等比缩小，其相对物距不变或增大、透视反向畸变加大。当形体等比缩小一定值时，其透视反向畸变为WMY。因此，两者表现在中国传统绘画透视（一幅画）中远视距的视点不动，等比缩小形体（建筑物等）视为WMY；等比放大形体为空间体（内有山、水、树木等），相对物距变小，此时景物“近大远小”。第四，以中国传统绘画（界画）主要表现建筑物透视的WMY物距为视点依据，减小焦距值，表现场景，以取得绘画（轴画）相同的透视效应。为此，在“近大远小”与WMY要处理好形体大小与物距的相对关系，是“龟纹图”在中国传统绘画透视应用上的扩展。通过焦距270毫米（单）建筑物斜线45°与 80毫米场景（同视点、视中线，不同物距、形体）一组数据，表现出绘画透视。因此，同轴数据组合与移轴（中轴线）数据变化，都产生各自透视效果。为此，透视变化规律在中国传统绘画中透视研究就显得重要。上面的数据是相对的，不同的物距与不同的形体大小；不同的物距与不同焦距等，通过数据了解其相互关系。

在视点移动观看二维轴画和观看三维空间实景有着本质差别。观看二维轴画是以观看者看完此画为前题条件，而视点、视距、视野、人眼的分辩率等因素则是必要条件。视点移动相对于轴画固定，而轴画的移动相对于视点的固定，都反映出视中线与画面垂直而不产生透视畸变，达到好的视觉感受。同样，在横轴长幅画面的绘画透视效果上，能从虚拟现实、摄影等单（视）点透视（焦点透视）得以解释和验证。物距和形体的大小决定了透视畸变与反向畸变，而透视畸变与反向畸变又表现在透视效应中。

从上述分析，相对物距的选择是关系到建筑物透视反向畸变与景物“以大观小”的适度。在远视距和视点确定后，充满视景框大致在270毫米焦距、斜线为 45°，其反向畸变与绘画中的透视基本相同。那么，要表现明代仇英《清明上河图》这样的场景，调整中视线并确立视点、物距后（焦距2000毫米∠PFA=35°）与其相对应的（建筑物）斜线约 35°（远视距立方体透视投影图相对应的边平行、长度差值等，在绘画中难以表现出），建筑物透视反向畸变就确定了。由于取景范围小相应减小焦距值至150毫米，以加大视角，而表现山川、树木等“近大远小”的场景透视关系。因此，要处理好建筑物与周围的场景透视关系，关键是相对物距选定以及焦距值确定，而构图则取决于视点位置。在这里画框长宽比不是问题，后期图像处理也可截取，何况绘画从意识上就加以“整合”、“旋转”、“ 截取”等。因此，无论是VIZ、3D MAX还是照相机，当视点、视距（物距）不变， 改变焦距，则其透视点不变（易造成透视点变化的假相）。视觉感受只有图像大小，无拉长或压缩变化[7]，这只是对形体不变（等比缩放）而言。

2.2.4 综合分析

在中国传统绘画中按透视分析，“以大观小”需用“远视距”；同时见到山前山后、屋舍院庭和后巷，以取得 “折高折远” 的俯视构图就需采用“高视高”的方式，这样既符合透视规律也符合人的视觉感受。仰角的使用在布局上受到局限，同时受到透视约束在视觉上和人文方面都不被中国传统绘画所接受。清代陈枚《月下赏梅》建筑和人物的透视反向畸变，物距明显至中、远视距。建筑物的斜线延长线出现汇聚，人物前后表现“近大远小”，其人物之间、建筑物之间以及人物与建筑物之间的比例合适。同样，陈枚的《麟趾贻休》只表现建筑的透视关系，而（多个）人物的平行排列（垂直于视中线）并不产生人物透视。在中国传统绘画中反映出画师对透视规律的掌握和运用程度。清代丁观鹏《太族始和图》的建筑群体的斜线延长线向右上角汇聚，其汇聚点（灭点）大致在（自然景物的）地平线上。同样，清代冷枚《避暑山庄图》运用传统界画表现建筑物并结合西方绘画透视构图。雍正年间，在西方画师影响下年希尧撰写了焦点透视绘画法的《视学》书籍。……为了适应中国观众的习惯，往往稍加调整，将焦点置于画幅比较远的地方[8]。

在中国传统绘画（轴画）中所表现的透视内容，用单点透视（焦点透视）就能表达。如，北宋张择端《清明上河图》，其建筑、人物等就是透视的具体表现。对于另一幅（乾隆年间仿本）《清明上河图》[9]其建筑群的斜线有汇聚的趋向，但各斜线的汇聚有交叉出现。再者，（城墙）斜线拉的过长。其在“整合”中汇聚点远离和高于地平线，对于这个问题画师也感觉到了，巧妙地画了一片白云加以遮视。这和盛唐172窟《西方净土变》等出现透视问题是一类的，而斜线的运用在透视上至关重要。就是连现代Photoshop高手也出现类似透视问题，有的还出自名家。北宋张择端《清明上河图》就处理得很好，巧妙地避开长斜线（指立方体斜线）在大场面的困扰，较多的运用短（斜）线、掩盖、隐藏、淡化等方法。这于绘画中表现皇宫大院、官府建筑、豪门庭院等直白线段有明显差异。因此，在这样大场面（轴画）、（远）视距范围上要处理好自然景物与建筑物的关系上，中国传统绘画大都采用少而短的斜线画法。

在中国传统绘画里，年希尧的焦点透视绘画法《视学》中的“线画法”普遍运用于清代宫廷建筑绘画中。在透视处理上，根据中国人文文化特点稍加调整，将汇聚点置于画幅外较远的地方。古代建筑工程图（宫观楼阁界画）并没有孤立发展其实用性，不同历史时期常与人物、山水相结合，展现其具有的艺术特性。晋唐催生了“宫观山水”；宋代开始了“楼阁界画”；元代出现了“界画楼台”；明清界画在新艺术潮流、审美风尚结合下，生成一些新样式。明代仇英《汉宫春晓图》则是以WMY为表现的，其建筑与家俱斜线运用多且较长。

2.3 建筑与家俱的WMY

从五代周文矩所绘的《重屏会棋图》中，就可看到其家俱的画法。周文矩以擅长绘界画楼台等生活题材画而知名。中国古代建筑、家俱绘画同样从意识上侧重于加大透视的反向畸变。清代龚贤《画诀》：“画屋要设以身处其地，令人见之皆可入也……画屋固不宜板，然须端正，若欹斜使人望之不安。”中国的绘画在很早就提出了朴素的透视原理[10]。由于受到中国地域文化影响，古人要求建筑物要画的四平八稳，其（两条）主线要横平竖直，在视觉上有稳定感。因此在中国传统绘画中建筑、家俱的表现多数采用横平竖直线，尤其宫廷、庙宇、大户人家等更是如此。同样，在汉字（方块字）教育上，孩子初学写字老师会教他们要“横平竖直”的规范，以打基础；在斜线上同样受到人文文化的影响，致使绘画中的斜线在各朝代、各画者、各幅画都有差异（斜线夹角度数）。应从中国传统绘画透视的总体看，其主要是符合透视规律，符合轴测透视表现。视点移动和中轴线（视中线）上视点移动都会使斜线的角度改变，这点在上面已有论述。在图1中，焦距10000毫米∠PFA8为55°。而在中国传统绘画中有部分是以斜线为 45°左右的 WMY。如，上述的明代仇英《汉宫春晓图》，要得到∠PFA8为45°这样的WMY就需调整视中线和中轴线上视点位置。同样，∠KFE约2°。这与上述情况相同，在远视距时EF视为水平线，何况此物距为趋近无限远。再如，图3唐代《宫乐图》场景中，桌面EFGA为平行四边形（与图1中E8F8G8A8的四边形表现完全一致），∠EGA=49°；用 3个等圆（圈）对不同位置人物头部测量比较，其结果相同。从“龟纹图”分析此图并不是“反透视现象”[11]也不会“上翻感”，更不能恣意曲解是儿童混沌时期画作！而是零点透视（轴测透视——WMY）。“近窄远宽”只是错视。因此，当调整中轴线上视点物距趋近无限远，焦距相应增加，可获得在一定斜度的斜线。这里本节以焦距10000毫米论述WMY。

图3 宫乐图

透视的产生和发展，与绘画、建筑艺术实践有着密切关系，并离不开科学[12]。根据“龟纹图”透视变化规律，当物距趋近于无限远时透视的反向畸变加大至极限图形图像，为WMY。在绘画中WMY常用于表现庭园、房内等小场景，无远景的画面中。因此也就没有表现“近大远小”的形式，这是（WMY）透视的一种特殊表现方式。通常对于（轴画幅面）在视角小取不下景物时，物距不变以减小焦距值来增大视角范围。中国传统绘画透视与透视图像基本一致，符合透视法则，符合透视变化规律，是科学的！认为这段物距中国画不符合透视的说法，是没有根据的。同样，中国传统绘画好像始终与科学的观念没有什么牵连，始终在走着一条相对“纯粹”的艺术之路，……[11]，更是没有根据。在造型艺术中，只要有空间图形便有透视存在其中，任何一位艺术家只要动笔空间里物体就存在透视关系正确与否的问题[13]。孔子有言“从心所欲不愈矩”，用这句话来形容界面创作的要义也许是比较适合的[8]。

宋代李高《听阮图》、明代杜堇《玩古图》等透视图为反向畸变图形。其中的家俱与场景的透视效应可划到远视距、超视距至趋近无限远的范围。那么，宋代刘松年《唐五学士图》的透视图在透视效应中则为WMY，其物距趋近无限远。同样，唐代《宫乐图》、元代《荷亭对弈图》、刘贯道《梦蝶图》和《消夏图》也表现这种透视关系。中国传统画论要求画家“以大观小，如观假山”，又要“目力有定所”，这就促使画家只有从无限高远的视点位置来俯瞰人间。而要画这样的建筑群，要见其结构的全貌还要见其“中庭后巷中事”，任何有限视距的定点透视实际上只会束手无策[14]。然而，在物距趋近无限远时用WMY来解决这类问题是简单而科学的方式。“近大远小”的透视规律是“龟纹图” 透视变化规律的基本规律。这对于科学的理解和解释中国传统绘画的WMY内容是极为重要的。

通常透视示意图一般都用轴测图的形式来表现。在传统中国绘画中更多地可以看到此种方法的运用，中国画中的界画就是用此法来表现建筑物与画面空间的[12]。因此， WMY时常在中国传统绘画中的表现和运用，是科学和准确的。WMY也常用于现代空间设计效果图，而且是全方位的。

3 结 束 语

1）中国（传统）绘画依据“龟纹图”，WMY对画面建筑物（水平线、垂直线、斜线）、建筑物与（自然）景物相互关系的科学验证和论述。再结合《中西方绘画透视效应研究》全面论证和确立了中国传统绘画透视的科学性。

2）西方透视学是不完整的，中国现代“龟纹图”的创立不但弥补了四、五百年前列奥纳多·达·芬奇（Leonardo Da Vinci）的形体透视与西方透视学的空缺区（段），并且扩展到两端的极限范围，使之成为完整的现代透视学（理论）。

3）现代“零点透视（轴测透视——WMY）”填补了“一点透视（平行透视）、二点透视（成角透视）、三点透视（倾斜透视）”的分类理论空白。也就是说，缺了（中国）现代“龟纹图”只用（西方）灭点透视是无法验证“零点透视（轴测透视）”。同样，也就无法解读中国传统绘画透视。换句话说，裸视视距的透视理念无法判解远视距至趋近无限远的透视畸变内容，即便搭乘“爱因斯坦光速列车”[11]也无法追解其中的“奥秘”，看不见中国人在无限深远处那美景画卷。（透视）画面必有“灭点”的观点已不成立。

4）“龟纹图”全面验证了中国传统绘画透视的科学性。新理论表明，现代透视就是对三维空间形体表面畸变变化的研究，进一步说也就是对形体表面微分平面在三维空间投影变化的研究，已突破了早期的“画框”模式。

5）从绘画创作到数码图层编辑都离不开视点的“整合”。同样，意识上的相对视点“整合”内容表现在二维面上则不能超出人的视觉承受范围。透视不仅属造型艺术，也是图学的重要内容，在高等院校中必然引起高度重视。

6）现代“龟纹图”明确表明了中国传统绘画透视效应，而“散点透视”是种猜想（假设）。未经过科学验证的猜想不能以结论方式加以定义（论）。中线透视现象（简称：JM线）[3]的群体效应，是从另一个侧面对心点的论证。因此，在WMY上可用JM线的群体效应对中国传统绘画心点进行科学、合理论证，这里就不赘述。

[1] 乌明韫. 工程图中透视图与轴测图的关系[C]//2007机械类课程报告论坛文集,北京: 高等教育出版社,2007: 229-234.

[2] 汪 恺. 技术制图国家标准宣贯教材[M]. 北京: 中国计量出版社,1997: 129-132.

[3] 乌明韫. 二维图像编辑中透视效应的研究[J]. 福建农林大学学报(哲学社会科学版),2009,12(4):98-105.

[4] 刘广滨. 绘画透视教程[M]. 南宁: 广西美术出版社,2007: 16-17.

[5] 白 璎. 艺术与设计透视学[M]. 上海: 上海人民美术出版社,2005: 22.

[6] 殷光宇. 透视[M]. 杭州: 中国美术学院出版社,1999: 2-22.

[7] 乌明韫. 建筑效果图中的透视效应[J]. 福建农林大学学报(哲学社会科学版),2005,8(3): 90-92.

[8] 李思训,卫 贤,郭忠恕,等. 中国山水界画通鉴——界画楼阁[M]. 上海: 上海书画出版社,2006:71-135.

[9] 《清明上河图》全图(乾隆年间仿本)[EB/OL]. 坚东网,http://www.zjdart.com/html/2008-12/170p9.html 2008-12-2/2010-01-25.

[10] 张晓按. 设计透视[M]. 长沙: 中南大学出版社,2005: 23.

[11] 袁运甫,刘 斌. 图像时空论——中国首届绘画博士班毕业论文集[M]. 济南: 山东美术出版社,2006: 37-86.

[12] 洪复旦. 透视学[M]. 沈阳: 辽宁美术出版社,2005:14-88.

[13] 何靖泉,温秋平,谷长林,等. 透视学[M]. 沈阳:辽宁美术出版社,2006: 13.

[14] 蒲新成. 绘画与透视[M]. 武汉: 湖北美术出版社,2007: 前言-105.