超空泡射弹动力学稳定性分析

张丁雄，侯 健

(海军工程大学，武汉 430033)

超空泡射弹将超空泡技术应用到水下射弹中。研究表明，利用超空泡技术进行减阻，可以使阻力降低90%以上，提高弹丸在水中运动的稳定性。弹丸在水中运动时，若出现角速度的初始扰动，弹丸尾部将与空穴下表面撞击并回弹，进而与空穴上边界表面撞击再回弹，这种非定常运动形态，可使其在前进中获得动态平衡，直到空穴变小，过渡到空穴下边界的一部分与物面滑行相切的形态，对这种运动形态的模拟计算表明，他在理论上也是成立的。本文通过对弹丸与空泡边界表面碰撞的动力学分析，得出弹丸外形设计对射弹运动稳定性的影响规律。

1 数学模型

根据文献［1］进行数学建模，为了简化问题，本文只对超空泡纵向稳定性进行研究。建立图1 所示的坐标系，(x，y，z，o)为定坐标系，(x1，y1，o1，)是以空化器中心为原点的动坐标系。其中，x1是弹丸运动的方向，弹丸在这个方向上做直线运动，任意小扰动后弹丸在y1方向产生1 个速度分量。

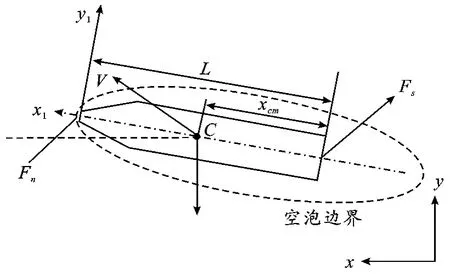
图1 超空泡射弹运动时力的分析

图1中:m 是弹丸的质量;L 为弹体全长;θ 为弹丸的轴线与水平线所成的夹角;ω 为转动角速度;α 为弹丸实际速度与轴线所成的夹角;xcm是重心距弹丸底部中心的距离;Fn为水对前端空化器的作用力;Fs为弹体尾部与空穴边界撞击时产生的水动力。

弹丸在水中运动时，在动坐标系中满足力的平衡方程:

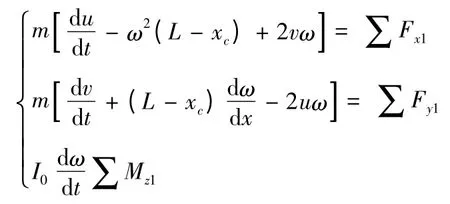
式中:I0为弹体绕重心C 的惯性矩(包括附连水惯性矩);u为x1方向上的速度分量;v 为y1方向上的速度分量。

由文献［1］可知，Fn在圆盘的纵轴线上。Fs可以分解为x1方向上的水阻力Fsx1和y1方向上的水撞击力Fsy1，见图2。Fn，Fsx1，Fsy1的大小可由文献［2］得到。

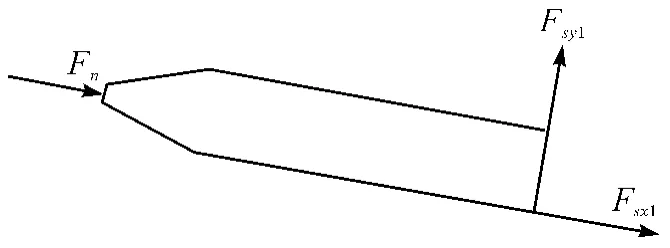
图2 作用于弹丸的水动力和撞击力

因为u2≫v2，ρAcku2≫2mLω2，lk/L≪1

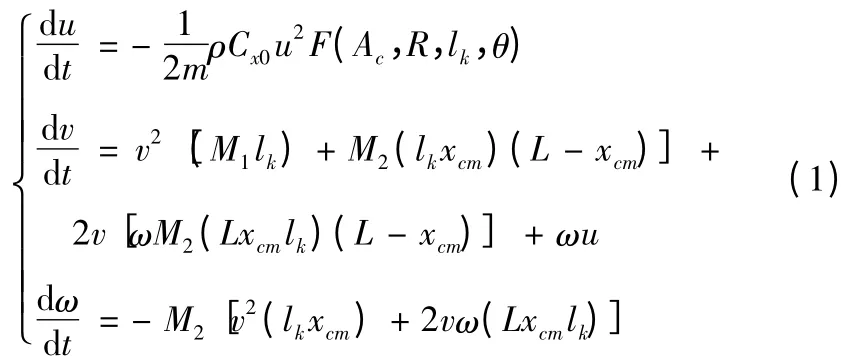
其中:

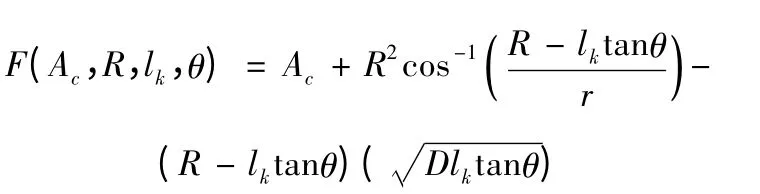
式中:Ac为圆盘空化器的面积;K 为与空化器形状有关的常数，当空化器为圆盘时，取2π;R 为射弹的半径;D 为圆盘的直径;ρ 为液体的密度;lk为弹体尾部浸湿水线长度。

空穴的长度一般相对于弹丸很大，故在弹体尾部与空泡壁发生碰撞的周围可认为空泡壁是水平的，假设此处的空穴轴向截面半径为Rk，弹丸的长细比为ε，如图3 所示。

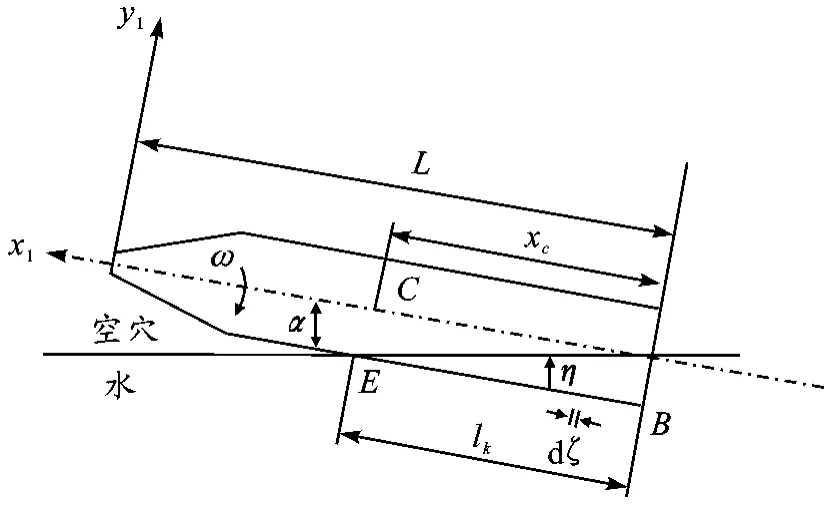
图3 撞击力的计算

当B 弹丸没有发生转动时，在坐标系ox1y1中，B 的坐标为(-L，-R)，经过旋转矩阵旋转后B 的坐标为(-Lcosα+Rsinα，-Lsinα-Rcosα)，又因为直线BE 斜率为tanα，故可求出直线方程为:

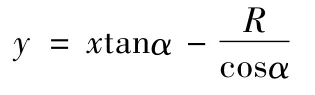
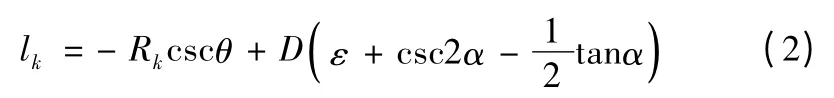
lk与α 的关系如图4 所示。

图4 扰动角与水线长度的关系

从图4 可以看出:当α 增大时，lk随之增大，即弹丸尾部与空穴壁的相交更加深入，与实际一致;当弹丸的细长比ε增大时，lk也随着增大。

设射弹绕流为理想可压缩流体无旋定常运动，为避免尾部空泡回注射流形成的数学奇异性，采用Riabushinsky 空泡闭合方式(即空泡以与射弹对称的形式闭合)，将坐标原点建立在空泡顶点处。

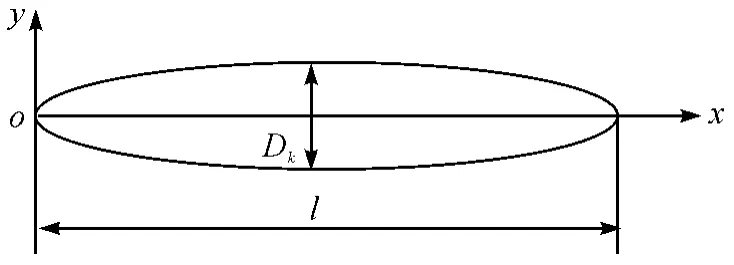
图5 超空泡外形

空泡外形方程为:

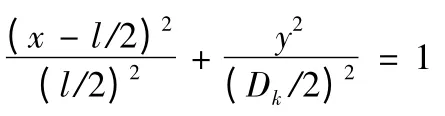
Dk和l 在文献中［3］中给出了研究者得出的多种经验公式，利用Matlab 将各种经验公式绘制曲线，如图6、图7 所示。

图6 空化数与空泡长度的关系

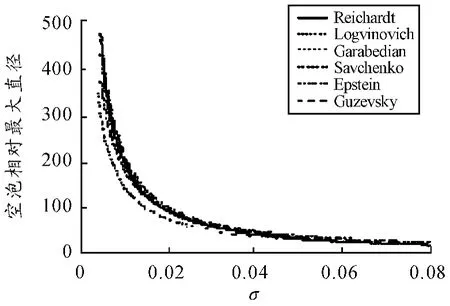
图7 空化数与空泡最大直径的关系

从图6、图7 可以看出，各超空泡外形计算公式在圆盘空化器情形时计算结果基本一致。

本文根据文献［4］和文献［5］，有:

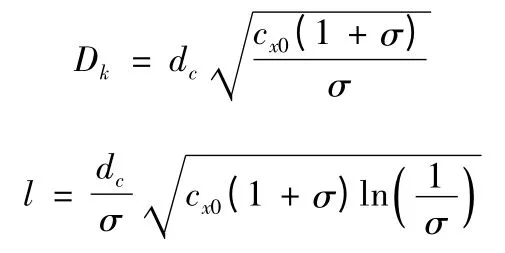
RE为椭圆空泡模型中E 点距长轴的距离。

因为θ 很小，当x=L 时，有

2 结果分析

1)当弹丸的细长比ε 增大时，由式(2)知，lk变大，故变大，即y1方向的加速度变大，弹丸在这个方向受到更大的回复力，所以弹丸更容易恢复到平衡位置，使得弹丸在水中运动的稳定性得以提高，这个结论在超空泡航行体外形设计中得到了广泛的应用。

2)由式(3)可知，当σ 减小时，Rk变大，故lk变小，ω 减小，所以从式(1)可以看出，当弹丸的发射速度变大时，空化数σ 变小，导致ω 变小，即弹丸的旋转角速度变小，有利于弹丸的稳定。

3 结束语

对超空泡射弹弹丸在水中的运行情况进行了数学建模，利用动力学和超空泡理论进行分析，得出了弹丸在动坐标系中的运动方程。

将弹丸产生的超空泡外形近似认为是1 个椭球体，利用超空泡流体理论建立了空泡外形方程。

对于高速超空泡射弹，可对弹丸外形进行合理设计使其在水中运行更加稳定。当弹丸的长细比较大时，细长弹丸在水中运动更平稳，这个结论与文献［6 -7］中得到的结果是一致的。

［1］王献孚.空化泡和超空化泡流动理论及应用［M］.北京:国防工业出版社，2009.

［2］Salil S Kulkarni，Rudra Pratap.Studies on the dynamics of a supercavitating projectile［J］.Applied Mathematical Modelling，2000(24):113-129.

［3］林明东，胡凡，张为华.超空泡航行体锥形空化器优化设计［J］.国防科技大学学报，2010(4):37-41.

［4］Garabedian P E. Calulation of axially symmetric cavities and jets［J］Pac.J.Math，1956，6(4):611-684.

［5］Logvinoich G V.Hydrodynamics of Flow with Free Boundaries［M］.Kiev:Naukova Dunka，1969.

［6］孟庆昌，张志宏，顾建农，等.超空泡射弹尾拍分析与计算［J］.爆炸与冲击，2009，29(1):56-60.

［7］李东旭.水下超空泡高速射弹数值分析与试验［J］.四川兵工学报，2010(6):31-35.