陆军船艇装备保障力量任务指派问题
刘增勇,邵鹏飞,陈祥斌,王 鹏,涂黎明
(1.军事交通学院 a.装备保障系; b.研究生管理大队,天津 300161;2.信阳军分区 潢川县人民武装部,河南 信阳 465150)
时效性是未来近岸岛屿联合作战船艇装备保障的显著特点之一,集中表现在保障力量的合理配置和恰当运用上,而恰当运用力量的关键就是任务的指派[1]。陆军船艇装备保障力量主要由岸基抢修保障机构、中继支援保障机构和机动伴随保障机构组成。战时这些机构都应配备一定数量的由具体专业维修人员和机动保障装备构成的机动( 巡回) 维修小组,其作用就是在一定的作战要求下,对参战陆军船艇装备进行伴随、巡回和支援维修[2]。为实现陆军船艇装备保障效益最佳,各机动维修小组的任务派遣优化问题就显得格外重要,因此有必要对保障力量的任务指派问题进行建模。
1 问题的提出与分析
已知某阶段陆军船艇装备保障机构有4 个机动维修小组( Ⅰ,Ⅱ,Ⅲ,Ⅳ) ,船艇编队在执行近岸岛屿联合作战输送任务过程中,有3 艘船艇( A,B,C) 出现故障,分别是主机滑油系统故障、船体多处损伤和高射机枪受击损坏。为确保任务顺利完成,装备指挥所命令保障机构必须及时派遣机动小组,在最短的时间内排除故障。作为指挥员应根据故障情况及所属机动小组的修理能力进行合理的任务指派,以确保排除故障的时间最短。
正如文中所描述的一样,装备战场抢修中首先考虑的就是怎样才能在最短时间内快速完成抢修任务,恢复装备的作战能力。因此,本文拟构建基于单目标的任务指派模型,以为陆军船艇战场抢修中保障力量的任务指派提供参考。
2 基于单目标的任务指派模型构建
2.1 问题描述
假设某陆军船艇装备保障机构有M 个机动维修小组,现要完成N 项任务,已知机动维修小组维修保障能力不尽相同,第 m 个小组完成第 n 项任务的时间为 tmn(m∈[1,M],n∈[1,N ]),tmn≥0( 单位:h) ,试确定使维修总时间T 最少的力量指派方法。设决策变量

2.2 任务指派类型分析与数学模型构建
下面根据战时陆军船艇装备保障力量任务指派可能出现的几种情况( 如表1 所示) ,分别建立其对应的数学模型[3]。
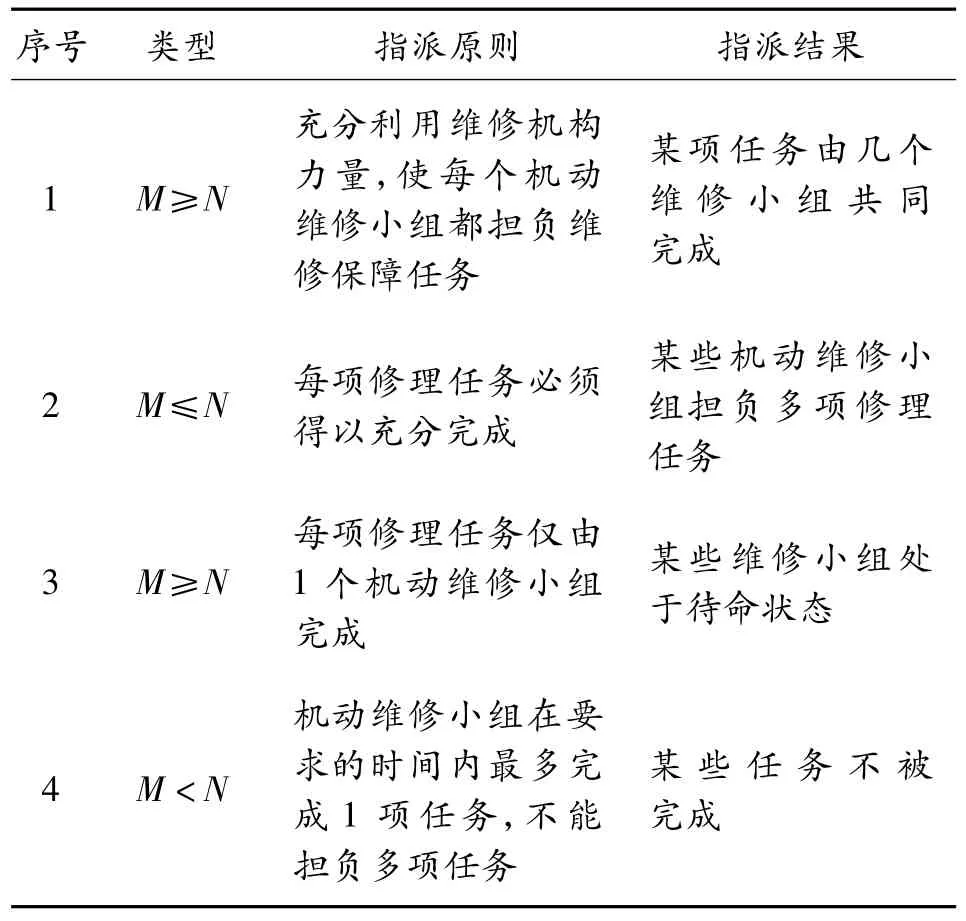
表1 修理任务指派类型
模型1 当M≥N,即机动维修小组数量大于( 或等于)修理任务数量时,装备保障指挥机构在进行修理任务指派中,考虑到充分利用维修力量,让每个维修小组都担负维修保障任务,则某项任务将由几个机动维修小组共同完成。其数学模型描述为:
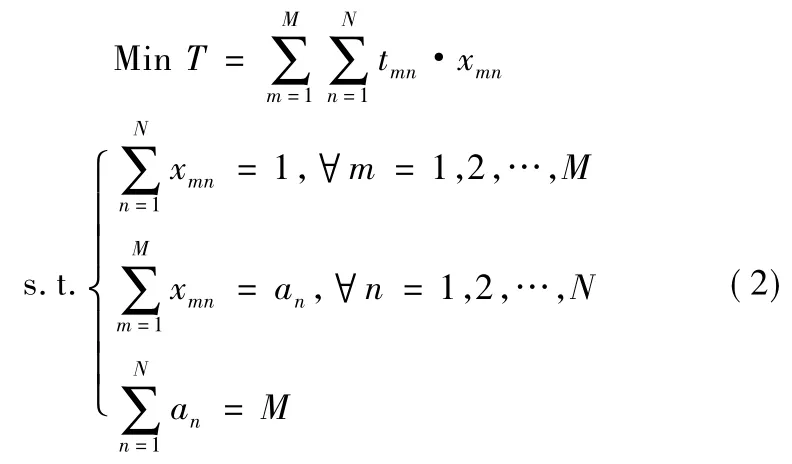
模型2 当M≤N,即机动维修小组数量小于( 或等于)修理任务数量时,装备保障指挥机构在进行修理任务指派中,考虑到每项任务必须得以圆满完成,则会出现1 个机动维修小组担负多项修理任务的情况。其数学模型描述为:

模型3 当M≥N,即机动维修小组数量大于( 或等于)修理任务数量时,装备保障指挥机构在进行修理任务指派中,考虑到每项修理任务仅由1 个维修小组完成,其他处于待命状态,应对应急保障任务。其数学模型描述为:
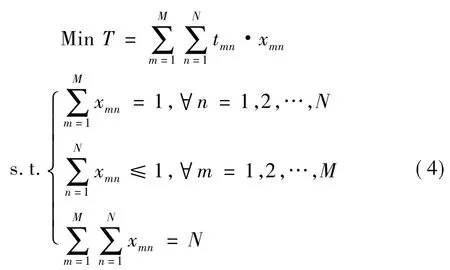
模型4 当M <N,即机动维修小组数量小于修理任务数量时,装备保障指挥机构在进行修理任务指派中,考虑到机动维修小组的维修能力有限,在要求的时间内最多完成1项任务,不能担负多项任务,则出现某些任务不被完成的情况。其数学模型描述为:

2.3 数学模型的求解算法
战时陆军船艇装备保障力量任务指派模型其实质是1种线性规划模型,求解线性规划模型的方法有多种,如表上作业法、图解法、单纯形法、人工变量法等[4]。目前解决单目标任务指派问题最常用的算法是“匈牙利算法”[5],基本思想是从系数矩阵( 即效益矩阵) 出发来确定最优指派方案,由于的1 行或1 列中只有1 个“1”,因此从矩阵的1行或1 列中减去任一常数K,则目标函数也相应减少K,这样以T 为目标的最优解和以T -K 为目标的最优解是相同的。用匈牙利算法解题时,要求修理小组数与任务数相等( M =N) 。因此解决上述几种修理任务指派模型,必须构造1 个广义的效益矩阵,使任务和维修小组具有一一对应关系。本文主要通过构造虚拟修理任务或虚拟机动维修小组,而后通过处理这些虚拟修理任务或机动维修小组的效益值,使其利于运用著名的“匈牙利算法”解题,同时又不影响真实机动维修小组的任务指派。
1) 模型1 的解法
对于模型1,M≥N,做如下处理:假定每项任务先安排1个小组完成,那么在剩下的M -N 个小组中,每个小组还可参与完成这N 项任务中的任何1 个,即每项任务最多还可能有M-N 个小组来完成。不妨假设每项任务都存在另外M-N个与之“完全等价”的“虚拟任务”,而每个小组完成这些等价任务的综合效益值完全一致; 这样,任务数就有将多于维修小组数量; 然后进一步假设还有个小组,他们完成任何任务的效益都最小。至此,在虚拟情况下,维修小组数便等于任务数,而且可以保证每项任务有且仅有1 个小组来完成。于是可构造适合传统匈牙利算法要求的扩展效益矩阵如下:
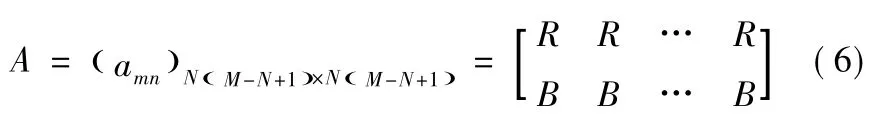
2) 模型2 的解法
对于模型2,M≤N,做如下处理:假定每个小组先安排1项任务,那么在剩下的N -M 个任务中,每个任务还可由M个小组完成,即每个小组最多还有N-M 项任务可指派。不妨假设每个小组都存在另外N-M 个功能条件与之“完全相同”的小组,而每项任务由这些“相同”的小组完成时的时间完全一致。这样,维修小组数就有将多于任务数; 然后进一步假设还有项“虚拟任务”,他们由任何维修小组来完成的效益值都最小。至此,修理任务数便等于机动维修小组数,而且可以保证每个小组完成且仅完成1 项任务。于是可构造适合传统匈牙利算法要求的扩展效益矩阵如下:
3) 模型3 的解法
对于模型3,M≥N,可分为2 种情况:①当M =N 时,可直接利用传统的匈牙利算法求解;②当M >N 时,维修小组数大于任务数量,应虚设M-N 项任务,构成1 个M×N 的效率矩阵,并且M 个维修小组在执行这M-N 项任务时的效率应该最低或者说时间最大,类似于模型1,在此不再展开。
4) 模型4 的解法
对于模型4,M <N,任务数量大于维修小组数量,可虚设N-M 个维修小组,构成1 个M×N 的效率矩阵,并且这NM 个维修小组在执行M 项任务时的效率应该最低或者时间最大,类似于模型2,在此不再展开。
3 举例验算
以模型1 为例,对问题进行单目标( 时间最短) 情况下的指派验证。假设各维修小组完成不同修理任务所需要的时间如表2 所示。
首先根据模型1 算法的解题思路,构造维修时间矩阵T,矩阵中行代表各机动维修小组,列代表修理任务。然后将矩阵T 根据模型1 的解法转换成广义的维修时间矩阵A,就可根据传统匈牙利算法解题步骤解题。
因此,本例的最优解是:第Ⅰ维修小组被指派完成B 任务,8 h 可完成;第Ⅱ和第Ⅳ维修小组被指派完成A 任务; 第Ⅲ维修小组被指派完成C 任务,8 h 可完成( 求解过程中的横线与纵线未画出) 。
4 结束语
装备保障能力是制约战争胜负的重要因素,而装备保障力量的任务指派问题则是合理利用装备保障力量、快速高效实施装备保障的关键所在。本文对陆军船艇装备保障力量的任务指派问题进行了分析,以保障时间最短为目标,构建了基于单目标的陆军船艇装备保障力量任务指派模型,给出了模型的求解方法,并对模型进行了举例验算。装备保障力量的任务指派受诸多因素的影响,对基于单目标( 时间最短)的陆军船艇装备保障力量任务指派问题的研究,能为战场抢修中装备保障力量的运用提供参考,也可起到抛砖引玉的作用,为多目标广义指派问题的研究奠定基础。
[1]刘广宇,齐艳平,龚传信,等.应抓好装备技术保障人力资源的优化配置[J].装备指挥技术学院学报,2001,12(4):91-94.
[2]许勇,金涛.模糊匈牙利算法在船艇抢修人员指派问题中的研究[J].军械工程学院学报,2006,18(5):51-53.
[3]张芳玉.战役通用装备维修资源保障研究[D].石家庄:军械工程学院,2005.
[4]钱颂迪.运筹学[M].北京:清华大学出版社,2005.
[5]刘建国,游伟,丁茹.战损装备应急抢修任务指派算法改进研究[J].军械工程学院学报,2006,18(4):51-53.

