基于集合映射的彩色图像边缘检测

孙 军，黎 琪，李和睿

(毕节学院 建筑工程学院，贵州 毕节 551700)

图像边缘检测是分割图像中不同事物的一种有效方法，它是计算机视觉研究的理论基础。目前的各种彩色图像边缘检测大多都是把彩色图像的RGB 3 个分量首先分别进行边缘检测，然后再合成一帧总的边缘检测图像。这些图像边缘检测方法建立在一维度的基础之上，能很好地与传统边缘检测方法结合起来，但在各RGB 彩色分量灰度变化不是很大的情况下，这些方法很难发挥很好的效果。

如果能考虑将彩色图像的颜色变化作为彩色图像边缘检测的依据，就可以克服彩色图像边缘检测的以上缺陷。本文把彩色图像具有的所有RGB 分量依次排列成为一个3 ×n矩阵，然后把这个矩阵的n 列与n 个连续实数一一对应起来，这样就把一帧三维彩色图像矩阵转化成为一帧一维实数矩阵，就可以充分利用彩色图像的颜色变化来实现彩色图像边缘检测。

支持向量机(support vector machine，SVM)是一种优秀的基于数据的机器学习方法，支持向量机不仅具有较强的推广能力，适用于小训练样本情况，而且具有强大的处理能力，对高维样本的处理复杂度与对低维样本近似，并能巧妙地引入核函数来实现非线性映射，从而完成非线性处理。支持向量机理论是结构风险最小化原理的近似实现，兼顾训练错误和泛化能力，解决了神经网络的难以确定网络结构、过学习和欠学习、局部极小点等问题。本文在实验中采用支持向量机建立n 列RGB 分量与n 个连续实数之间的映射函数对应关系，并在此基础上实现三维彩色图像矩阵到一维实数矩阵之间的转化。

1 RGB 分量与连续实数之间的对应

在彩色图像的RGB 分量中，对应的灰度级为0 到250 之间的整数，不同灰度级的RGB 分量合成彩色图像的不同颜色，不同颜色的RGB 分量的分别排列为

其中，式(1)为3 行2513列的矩阵。令

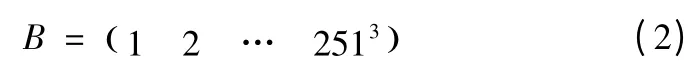
这样就可以建立矩阵A 和矩阵B 之间的函数对应关系。由于支持向量机可以在小样本的情况下学习矩阵A 与矩阵B 之间的这种函数对应关系，所以本文在采用小样本的情况下，使用支持向量机来拟合这种函数对应关系。

2 支持向量机的算法构造令

x=(x1，x2，…，xl)，xi(i=1，2，…，l)为在式(1)中按一定间隔抽取到的列向量;令X=(y1，y2，…，yl)，其中yi(i=1，2，…，l)为式(2)中对应的整数。这样就得到训练集组

选择支持向量机的核函数K(xi，xj)，i，j =1，2，…，l。把T 代入式(4)，选择适当的参数ε ＞0 和惩罚参数C ＞0，就可以构造并求解凸二次规划问题

求解式(4)得解

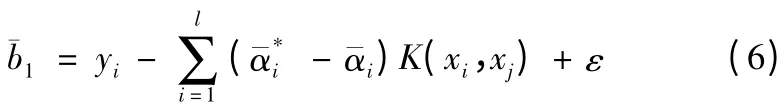
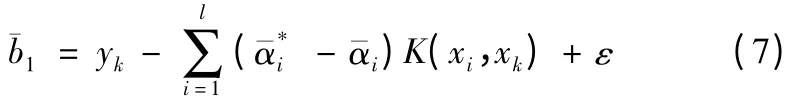
构造决策函数

决策函数式(8)就是式(1)与式(2)之间的映射函数对应关系，通过式(8)就可以把彩色图像的RGB 分量矩阵转化一维实数矩阵。通过这个一维实数矩阵，就可以在彩色图像颜色变化的基础上，对不同的彩色图像进行边缘检测。3 实验和证明在式(1)中分别提取出抽样样本和测试样本2 组不同的数据，抽样样本用于构造支持向量机决策函数式(8)，测试样本用来对支持向量机决策函数的精度进行检测，通过精度检测来确定凸二次规划问题式(4)中的最佳参数ε ＞0 和惩罚参数C ＞0。具体实现步骤如图1 所示。

本文采用一张普通照相机拍摄的JPG 照片作为实验对象，用上述方法构造的决策函数实现JPG 图像的RGB 分量矩阵到一维实数矩阵之间的转化，然后再作相应的一维实数矩阵数据平滑处理，最后再对一维实数矩阵进行边缘检测。以下分别是本文实验用的原始图像，用Canny 算子对原始图像进行边缘检测的结果，本文算法对原始图像进行边缘检测的结果。

实验表明:在选择适当参数的情况下，本文算法得到的彩色图像边缘检测效果，明显优于canny 算子彩色图像边缘检测的效果。

图2 彩色图像边缘检测结果比较

3 结束语

支持向量机具有很好的泛化能力(generalization ability)，能有效克服传统近似几何校正算法中的法方程病态性的问题，以及传统近似几何校正算法基于线性算法、非线性算法的最小二乘算法的过学习、泛化能力差、法方程病态性、矩阵奇异性、对初始解敏感性、要求足够多控制点等缺陷。本文使用支持向量机建立RGB 三维矩阵与一维实数矩阵之间的集合映射函数关系，实现彩色图像RGB 三维矩阵到一维实数矩阵之间的转化，并在此基础上利用上彩色图像的颜色变化实现图像边缘检测，实验表明这种彩色图像边缘检测效果明显优于传统的彩色图像边缘检测效果。

［1］李明，蔡询.基于支持向量机的多特征彩色图像边缘检测［J］.计算机工程与设计，2012，33(2):639-643.

［2］孙军，黎琪，李和睿.QuickBird 遥感图像校正模型研究［J］.四川兵工学报，2012，33(4):106-108.

［3］Kenneth R.Castleman.数字图像处理［M］.北京:电子工业出版社，2011.

［4］邓乃扬，田英杰.支持向量机:理论、算法与拓展［M］.北京:科学出版社，2009.