基于锁放干扰力矩作用的摆式陀螺仪动力学建模

孙立江，常振军，贾天龙

(1.第二炮兵工程大学 二系，西安 710025;2.解放军边防学院 司令部工作教研室，西安 710108)

目前，国内陀螺寻北仪在整个寻北过程中，需多次锁放陀螺，目前完成一次锁放通常需要约1 min，而Gyromat 3000一次锁放仅需十几秒，速度很快，且陀螺灵敏部的稳定性好［1-3］，因此，锁放的快慢和陀螺灵敏部的稳定性直接影响寻北时间，这就需要进行摆式陀螺仪在锁放干扰力矩作用下的动力学建模。

1 摆式陀螺仪结构与寻北原理

1.1 摆式陀螺仪结构

摆式陀螺寻北仪如图1 所示，由与外壁固连的金属悬挂带、陀螺房壳、陀螺转子及配重等组成［4］。其中金属悬挂带一般由镍铬等合金材料构成，具有较好的弹性特征和较高的抗拉强度;陀螺房壳中装有陀螺转子，房壳起到保护和屏蔽的作用，陀螺转子装在万向支架上，具有3 个方向的自由度。配重使转子缺少1 个方向上的自由度。在平时存放时，由下面支撑装置将整个陀螺灵敏部托起;工作时灵敏部下放，由悬挂带吊起，进行寻北。

图1 摆式陀螺仪结构

1.2 摆式陀螺仪寻北原理

如图2 所示，设初始位置陀螺灵敏部的重力P 通过悬挂带与陀螺房连接点O 和重心位置G，此时重力不产生力矩，转子也不发生进动。当地球自转了β 角时，转子轴相对水平面也抬高了β 角，这时陀螺仪的重力P 产生了力矩，l 为悬挂带下悬挂点至重心的距离，称为倾心高，由陀螺进动规律知，该力矩作用在陀螺转子轴上，将产生进动。而对于指定的陀螺仪，它的P、l 和动量矩H 都是固定的，进动角速度ωP只由角度β 决定，而β 的变化却是由地球自转所造成的，也就是说，是由地球自转和重力矩的综合作用，使陀螺转子轴发生进动。由于重力矩的方向指向北方，这样总有一个指向真北的外力矩作用在陀螺灵敏部，使陀螺的动量矩沿最短路径向真北方向进动。

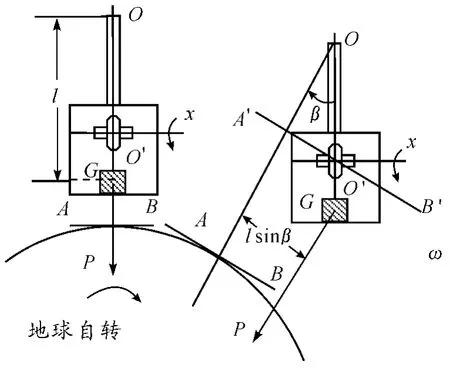
图2 摆式陀螺寻北原理

2 基于动静法的摆式陀螺仪动力学建模

依据力学中的达朗伯原理，将牛顿第二定律F =ma 变换为F+Q=0，Q= -ma 表示物体的惯性力，一般为相对惯性力、牵连惯性力和哥式惯性力三者的矢量和，如此可使动力学问题转变为静力学问题求解，从形式上把受力运动状态转为受力平衡状态，这种处理问题的方法称为动静法或惯性力法［5］。

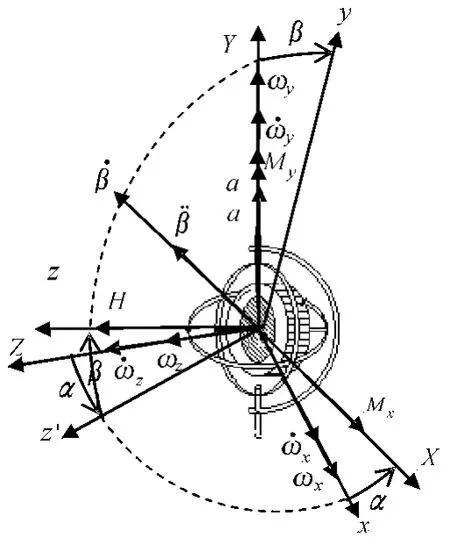
图3 动坐标系下陀螺仪运动

同时假设地理坐标系相对惯性坐标系转动的角加速度(角速度)在地理坐标系各轴上的投影分别为和(ωx、ωy和ωz)。由于陀螺仪具有绕Ox 轴和Oy 轴的转动惯量Ix和Iy，当陀螺仪绕这两轴出现角加速度时，就有一般定轴转动刚体的转动惯性力矩。转动惯性力矩的方向与角加速度方向相反，如图4 所示。当陀螺仪相对地理坐标系的转角α 和β 均为微量时，转动惯性力矩为

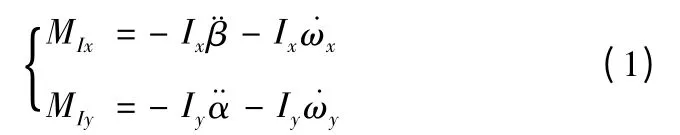
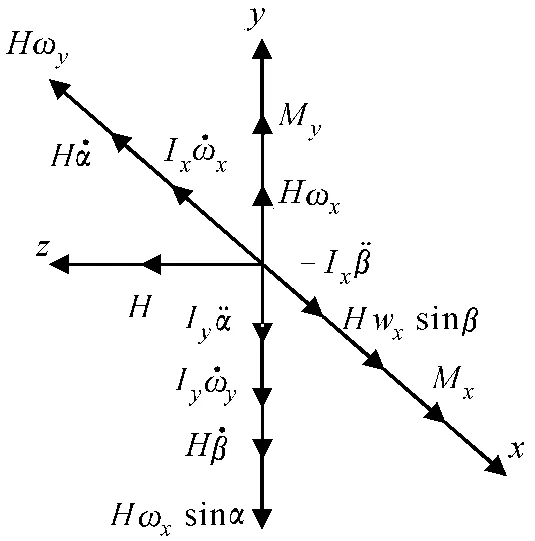
图4 惯性力矩之间的关系

根据动静法(或惯性力法)原理，在作用于物体的外力之外，另加上惯性力，即可是动力学问题转变为静力学问题求解。将式(1)和(2)相加，可以写出陀螺仪绕内环轴和外环轴的力矩平衡方程式

整理得

由图5 将地球自转角速度分解到地理坐标系中，并结合图3 各轴关系，得到

其中φ 为当地纬度。地理坐标系的角加速度为零，将式(5)代入式(4)中得到

式(6)为利用动静法建立的摆式陀螺寻北运动方程。

图5 地球自转角速度分解

3 摆式陀螺仪在受锁放干扰力矩影响下的动力学模型的建立

在锁放过程中，由于摆式陀螺仪的陀螺灵敏部整体的质量由锁紧机构来进行承受，陀螺灵敏部上端的吊带所承受的陀螺灵敏部的质量在下放过程中，随着陀螺灵敏部的下放是从零逐渐增大直至整个承受陀螺灵敏部的质量。由于锁放力矩总是在t=0 时加到陀螺仪上的，这个力矩可看成是阶跃的常值力矩，为了分析方便，假设只在陀螺仪的内环轴上作用有该常值力矩Mx。而锁放干扰力矩虽然是直接作用与陀螺房，但是，可认为是瞬时对陀螺仪的干扰，故可近似认为是脉冲力矩。又由于脉冲力矩的作用时间短，可认为陀螺仪主轴的初始方位不发生改变，故该力矩作用以后陀螺仪上将不会有外力矩变化，但是会引起陀螺仪主轴初始角速度的变化［6］。下面就以下放过程为例来进行分析摆式陀螺仪在干扰力矩作用下的动力学模型。而陀螺灵敏部的锁紧过程的分析方法与此相同。

3.1 吊带不受力

在此情况下，根据前面动静法所建立的陀螺仪的动力学模型公式可得到

3.2 吊带开始受力，但未全部承受陀螺灵敏部的质量

此时，虽然吊带开始受力，但是，陀螺仪在吊带和下放力矩的共同作用下处于力矩平衡状态，因此，根据前面动静法所建立的陀螺仪的动力学模型公式可得到

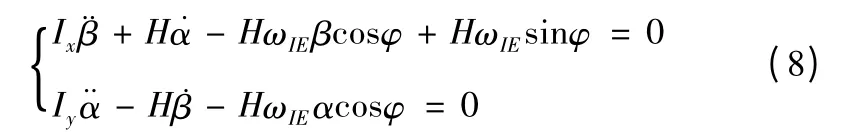
3.3 吊带完成承受陀螺灵敏部的质量

此时只受锁放干扰力矩的影响。吊带在x 轴方向的力矩为:MD=Tlsin(β-γ)。同样，根据前面动静法所建立的陀螺仪的动力学模型公式可得到

这样所得到的式(7)、式(8)和式(9)就是在受锁放干扰力矩影响的摆式陀螺仪的动力学模型。

4 结束语

本文从摆式陀螺仪的结构和寻北原理出发，利用动静法建立了摆式陀螺仪的动力学模型，并以此为基础，分析了在锁放过程中摆式陀螺仪在受锁放干扰力矩影响下的运动情况和受力情况，并建立了在此过程中的动力学模型。

［1］DMT GmbH.Exploration＆Geosurvey［EB/OL］.［2009 -07-24］.http: // www.gyromat.de.

［2］万朋，张海东.陀螺经纬仪零位改正系数研究［J］.北京测绘，2005(2):48-49.

［3］刘勇，张志勇，冯伟利.陀螺经纬仪校准技术［J］.宇航计测技术，2007(4):6-10.

［4］姜春福.悬挂式二自由度陀螺经纬仪运动规律的研究［D］.北京:北京工业大学，2000.

［5］刘延柱.陀螺力学［M］.2 版.北京:科学出版社，2009:67-69.

［6］许江宁，卡鸿巍，刘强，等.陀螺原理及应用［M］.北京:国防工业出版社，2009:46-49.