功能梯度界面层模型断裂问题研究进展

邸 克，杨月诚

(第二炮兵工程大学 601 室，西安 710025)

随着科技的发展，先进材料的应用越来越广泛，当他们因为某些工程需要而黏结在一起时，其界面力学问题也日益成为学者们关注的热点。人们为了有效地分析界面力学问题，评估结合材料的强度或寿命，提出了许多界面力学模型。其中，有一类功能梯度界面层模型是在实验基础上提炼而来的，在表征界面力学行为方面适应工程研究需要，具有广泛的发展前景。本文简要介绍功能梯度界面层模型，并对该模型断裂问题的研究现状和研究方法进行相应的探讨。

1 功能梯度界面层模型简介

值得注意的是，以上几类界面模型均在一定程度上表征了界面力学行为，但尚未考虑真实界面黏结结构，即缺乏相应的实验依据。1988 年，Delale 和Erdogan［8］依据界面两侧不同材料在细观层面的相互扩散和渗透，提出了功能梯度界面层模型(也称为非均匀界面层模型)，该模型将原界面区域看成很薄的功能梯度材料，而两侧均匀材料的弹性模量和泊松比在界面层中以指数函数形式连续过渡(如图2)。这种界面结合部材料力学属性随界面层厚度呈梯度变化的特性已被相应的实验证实［9］，因此，该模型具有一定的实验基础，在表征界面黏结结构时符合实际。此外，该模型还可有效消除裂纹尖端附近应力的振荡性，避免裂纹两侧材料相互嵌入的不合理现象，在对应力强度因子等断裂参量进行计算时，符合物理规律。

图1 理想界面模型

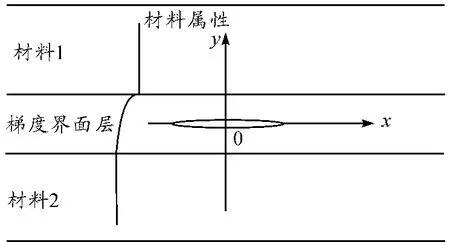
图2 功能梯度界面层模型

2 模型断裂问题

2.1 研究概述

目前，人们对含功能梯度材料的各种结构力学性能进行了大量研究，比如功能梯度涂层、壳以及板条等，相比之下，直接对功能梯度界面层的研究较少。但是，由于对均匀材料各种力学特性的研究已基本成熟，在分析功能梯度界面层模型时，其核心是两均匀材料之间的功能梯度材料层，因此对功能梯度材料力学特性的研究成果可较为方便地应用到功能梯度界面层中。

2.2 模型断裂问题的分类

人们为了有效研究功能梯度界面层的断裂力学特性，一般采用特定的函数表示界面层内力学属性的分布规律，而且多以理论推导的方式开展该领域的研究工作。按照界面层内所划分层数的差异，功能梯度界面层模型可分成单层模型、互扩散(2 层)模型和分层(多层)模型。

1)单层模型

在功能梯度界面层模型发展的早期，界面层一般采用某种函数表征力学属性(比如模量和密度)的分布，这也可称为单层模型。其中应用最多的是指数函数，比如将界面层弹性模量(或剪切模量)μ2写成以下形式

应用该指数型界面层模型，Erdogan 等开展了大量的工作，研究了平面［8］、反平面［10-11］和轴对称［12］等状态下的裂纹问题。Fildis 和Yahsi［13］研究了轴对称条件下Ⅰ、Ⅱ和Ⅲ型裂纹问题;Babaei 等［14］采用Laplace 变换方法，讨论了界面层中裂纹在动态冲击载荷下的响应;Shbeeb 等［15］考虑界面层的平面裂纹问题，得到了应力强度因子和应变能释放率。

为了更广泛地表征功能梯度材料属性，人们也尝试用其他函数描述材料参数的变化。值得注意的是，这些函数不是任意选取的，而是要满足控制微分方程有解析解的原则。Wang 等［16-19］采用一种幂律函数表示界面层中材料属性的分布，这时，界面层内模量μ2写为

1.2.3 评价指标 ①6个月前后护士跌倒知识、态度、行为测评问卷:问卷在参考相关文献及咨询有关护理专家的基础上设计而成，并进行前期预试验，内容包括跌倒相关知识15项条目、对跌倒重视程度及认识10项条目、跌倒预防实施行为10项条目组成。分值越高，表示护士跌倒预防知识、态度、行为实施越好。②6个月前后患者跌倒预防认知度和预防措施满意度调查问卷，内容包括跌倒预防措施认知度12个条目和预防跌倒措施落实的满意度7个条目，分值越高，表示患者跌倒预防措施认知度和措施落实满意度越好。

另外，Cheng 等［22］将界面层内模量假设成纵坐标的倒数函数，其具体形式为

2)互扩散模型

Li 等［23］考虑了界面两侧材料之间扩散性能的差异，提出了1 个互扩散界面层模型。该模型采用2 种函数描述界面层的材料属性变化，相对之前1 种函数形式的界面层模型来讲，互扩散模型可更方便地表征界面层材料参数的非单调变化特性。

3)分层模型

真实情况下，由于设计或制造时各种因素的影响，功能梯度材料的参数变化可能是任意形式。因此，当参数任意变化时，不管是用单层模型表征，还是用互扩散模型描述，都难以达到较高的精度。为此，人们发展了一种分层模型来表征功能梯度材料属性。该模型将功能梯度材料划分成有限多个子层，在每个子层中用特定函数表征材料属性。对于功能梯度界面层来讲，人们主要采用常数［24-30］或线性函数［31-35］表示子层内材料属性的分布规律。此外，人们对功能梯度板条、涂层等结构进行研究时，将功能梯度材料分成多个子层，并把每一子层内材料属性设定为指数［36］或倒数［37］形式，这些方法也较容易在功能梯度界面层中得到应用。

除了上文介绍的理论研究之外，采用数值方法直接对功能梯度界面层裂纹问题进行研究较为少见。但是，人们对含裂纹的功能梯度材料进行了有限元数值计算［38］，该成果对有限元数值方法在功能梯度界面层中的应用有一定的借鉴意义。

3 模型断裂问题理论研究方法

目前，人们对功能梯度界面层裂纹问题进行理论分析时，已经形成了一套较为成熟的方法。下面以单层指数型界面层模型反平面裂纹问题［39］为例进行说明。

首先通过反平面问题的平衡方程和本构方程得到控制方程:

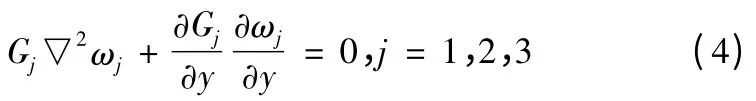
式中:Gj为各层材料的剪切模量;ωj为位移分量。

将式(4)进行Fourier 变换可得

式中，Fourier 变换可定义为

求解微分方程(5)，再结合本构方程可以得到Fourier 变换域中应力τj和位移ωj的关系。

引入以下形式的位错密度函数

式中:Δω2表示裂纹面上的位移增量。

由以上相关公式可推导出Cauchy 型奇异积分方程

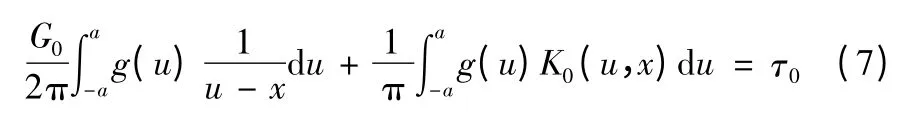
式中:G0和τ0分别是裂纹面处的剪切模量和应力载荷;a 是裂纹长度的1/2。

该奇异积分方程可以在结合位移单值条件后通过配点数值方法［39］求解，在得到位错密度函数g(x)的数值解后即可获得应力强度因子等断裂参量。

4 结束语

本文对功能梯度界面层模型断裂问题研究现状及研究方法进行了介绍。该模型与其他界面力学模型相比，可充分考虑界面黏结处细观结构的影响。目前，对该模型的研究主要以理论方法开展，而且为了得到理论解，模型中许多参数均设置为理想状况，因此，该模型在实际应用方面还有一些欠缺。在此后的研究中，该模型应结合有限元等数值方法加以扩展，使其在表征实际界面力学行为方面产生更好的应用效果。

［1］Williams M L.The stresses around a fault or crack in dissimilar media［J］. Bulletin of the Seismological Society of America.1959，49(2):199-204.

［2］England A H.A crack between dissimilar media［J］.Journal of Applied Mechanics，1965，32(3):400-402.

［3］Atkinson C.On stress singularities and interfaces in linear elastic fracture mechanics［J］.International Journal of Fracture，1977，13(6):807-820.

［4］Comninou M. The interface crack［J］. Journal of Applied Mechanics，1977，44(4):631-636.

［5］Comninou M.The interface crack in a shear field［J］.Journal of Applied Mechanics，1978(45):287-290.

［6］Comninou M，Schmueser D.The interface crack in a combined tension-compression and shear field［J］. Journal of Applied Mechanics，1979(46):345-348.

［7］Mak A F，Keer L M，Chen S H，et al. A no-slip interface crack［J］. Journal of Applied Mechanics，1980( 47): 347-350.

［8］Delale F，Erdogan F.On the mechanical modeling of the interfacial region in bonded half-planes［J］. Journal of Applied Mechanics，1988，55(2):317-324.

［9］Monclus M A，Young T J，Maio D D. AFM indentation method used for elastic modulus characterization of interfaces and thin layers［J］.Journal of Materials Science，2010(45):3190-3197.

［10］Erdogan F，Kaya A C，Joseph P F.The Mode Ⅲcrack problem in bonded materials with a nonhomogeneous interfacial zone［J］. Journal of Applied Mechanics，1991( 58): 419-427.

［11］Ozturk M，Erdogan F. Antiplane shear crack problem in bonded materials with a graded interfacial zone［J］.International Journal of Engineering Science，1993，31(12):1641-1657.

［12］Ozturk M，Erdogan F.An axisymmetric crack in bonded materials with a nonhomogeneous interfacial zone under torsion［J］.Journal of Applied Mechanics，1995(62):116-125.

［13］Fildis H，Yahsi O S.The axisymmetric crack problem in a non-homogeneous interfacial region between homogeneous half-spaces［J］. International Journal of Fracture，1996(78):139-164.

［14］Babaei R，Lukasiewicz S A.Dynamic response of a crack in a functionally graded material between two dissimilar half planes under anti-plane shear impact load［J］.Engineering Fracture Mechanics，1998，60(4):479-487.

［15］Shbeeb N I，Binienda W K，Analysis of an interface crack for a functionally graded strip sandwiched between two homogeneous layers of finite thickness［J］.Engineering Fracture Mechanics，1999(64):693-720.

［16］Wang X Y，Wang D.On the Griffith crack in a nonhomogeneous interlayer of adjoining two different elastic materials［J］. International Journal of Fracture，1996( 79): R51-R56.

［17］Wang X Y，Zou Z Z，Wang D.On the penny-shaped crack in a non-homogeneous interlayer under torsion［J］.International Journal of Fracture，1996(82):335-343.

［18］Wang X Y，Zou Z Z，Wang D.On the penny-shaped crack in a nonhomogeneous interlayer of adjoining two different elastic materials［J］. International Journal of Solids and Structures，1997，34(30):3911-3921.

［19］Zou Z Z，Wang X Y，Wang D.On the modeling of interfacial zone containing a Griffith crack:plane problem［J］.Key Engineering Materials，1998(145-149):489-494.

［20］Li C，Duan Z，Zou Z.Torsional impact response of a pennyshaped interface crack in bonded materials with a graded material interlayer［J］.Journal of Applied Mechanics，2002(69):303-308.

［21］Choi H J.Impact response of a surface crack in a coating/substrate system with a functionally graded interlayer:antiplane deformation［J］. International Journal of Solids and Structures，2004(41):5631-5645.

［22］Cheng Z Q，Zhong Z.Fracture analysis of a functionally graded interfacial zone between two dissimilar homogeneous materials［J］.Science in China Series G:Physics，Mechanics ＆ Astronomy，2006，49(5):540-552.

［23］Li Y D，Lee K Y.Mechanical modeling and transient antiplane fracture analysis for the graded inter-diffusion regions in a bonded structure［J］. Meccanica，2009 ( 44): 389-408.

［24］Itou S，Shima Y.Stress intensity factors around a cylindrical crack in an interfacial zone in composite materials［J］.International Journal of Solids and Structures，1999(36):697-709.

［25］Itou S.Stress intensity factors around a crack in a nonhomogeneous interfacial layer between two dissimilar elastic halfplanes［J］. International Journal of Fracture，2001(110):123-135.

［26］Itou S. Transient dynamic stress intensity factors around a crack in a nonhomogeneous interfacial layer between two dissimilar elastic half-planes［J］. International Journal of Solids and Structures，2001(38):3631-3645.

［27］Itou S.Thermal stresses around a crack in the nonhomogeneous interfacial layer between two dissimilar elastic halfplanes［J］. International Journal of Solids and Structures，2004(41):923-945.

［28］Itou S. Stress intensity factors around a moving Griffith crack in a non-homogeneous layer between two dissimilar elastic half-planes［J］. Acta Mechanica，2004( 167): 213-232.

［29］Itou S.Stress intensity factors for a moving cylindrical crack in a nonhomogeneous cylindrical layer in composite materials［J］.Archive of Applied Mechanics，2005(75):18-30.

［30］Itou S.Transient dynamic stress intensity factors around two rectangular cracks in a nonhomogeneous interfacial layer between two dissimilar elastic half-spaces under impact load［J］.Acta Mechanica，2007(192):89-110.

［31］Wang Y S，Gross D. Analysis of a crack in a functionally gradient interface layer under static and dynamic loading［J］. Key Engineering Materials，2000( 183 - 187): 331-336.

［32］Wang Y S，Huang G Y，Gross D.On the mechanical modeling of functionally graded interfacial zone with a Griffith crack:anti-plane deformation［J］. Journal of Applied Mechanics，2003(70):676-680.

［33］Huang G Y，Wang Y S.A new model for fracture analysis of a functionally graded interfacial zone under harmonic antiplane loading［J］. Engineering Fracture Mechanics，2004(71):1841-1851.

［34］Huang G Y，Wang Y S，Yu S W. Fracture analysis of a functionally graded interfacial zone under plane deformation［J］. International Journal of Solids and Structures，2004(41):731-743.

［35］Wang Y S，Huang G Y，Gross D.On the mechanical modeling of functionally graded interfacial zone with a Griffith crack:plane deformation［J］.International Journal of Fracture，2004(125):189-205.

［36］Guo L C，Noda N.Modeling method for a crack problem of functionally graded materials with arbitrary properties—piecewise-exponential model［J］. International Journal of Solids and Structures，2007(44):6768-6790.

［37］Cheng Z Q，Meguid S A，Zhong Z.Thermo-mechanical behavior of a viscoelastic FGMs coating containing an interface crack［J］.International Journal of Fracture，2010(164):15-29.

［38］Kim J H，Paulino G H.Finite element evaluation of mixed mode stress intensity factors in functionally graded materials［J］. International Journal for Numerical Methods in Engineering，2002(53):1903-1935.

［39］Erdogan F，Gupta G D.On the numerical solution of singular integral equations［J］. Quarterly of Applied Mathematics，1972，29(4):525-534.