新型破甲杀伤双用途子母弹对典型目标射击效力仿真

陶海军，吴晓云，仇 磊

(陆军军官学院，合肥 230031)

国产某火箭炮武器系统配备了新型破甲杀伤双用途子母弹作为其主力弹种，该型子母弹射程远、威力大，主要用于打击战役战术纵深内的高价值目标。由于其造价十分昂贵，所以不论在平时还是在战时，都不可能像普通火炮那样大量发射炮弹用于检验射击效力，所以要评估其射击效力，只能采用预测或预估的方法。目前采用的解析法，如相当“榴弹”法、母弹(子弹)积分法等，这些方法都没能较好地克服子母弹的“毁伤重叠”问题。而Monte-Carlo 法，具有随机事件仿真的功能，它是以高容量和高速度的计算机为前提条件的，是一种计算机上的随机实验，即在计算机上的“打靶”。我们可以在计算机上对一个目标“发射”几百枚至上千枚“火箭弹”，据其统计的“射击”结果，就能具有很高的可信度及精度，用这样的结果还可以检验或修正解析算法的结果和模型。

1 基本模型

仿真法建立的数学模型大多与解析法不同，但也有相似和借用之处，尽管2 种方法分析思路不同，但都根植于射击的事理，因此有些模型，2 种方法都可使用。

1.1 目标仿真

目标仿真就是将目标的实际面积转化为它的等效圆来处理。目标区系平面直角坐标系，以中心为目标位置(或面目标中心位置)，各目标在该坐标系中的描述方法为:

1)点目标。面积Ld× Lf，则先计算目标等效圆，半径在坐标系xoy 中的方程:设点目标中心位于原点位置，有单个面目标也可按上式表示。其他目标如线状目标也按点目标的描述方法，体现其形状特点。

2)集群目标。集群目标是由若干个单位目标组成的。设某单位目标的中心位置为(xTj，zTj)，(j =1，2，…，M);其中M 为集群目标中的单位目标数，j 为单位目标序号，RTj为第j个单位目标的等效圆半径，则各单位目标按下列方程描述。

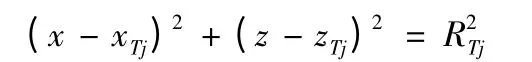
1.2 单发母弹(子弹散布中心)仿真

以远程火箭炮单炮对目标的瞄准点作为母弹(子弹散布中心)的理想落点，再根据火箭弹CEP，即可仿真母弹(子弹散布中心)的实际落点。还可以根据射击误差分组情况，由诸元误差的方差和散布误差的方差分步来进行仿真。

1.3 子弹炸点(落点)仿真

子弹炸点(落点)的仿真，按照远程火箭炮的特点，在单发母弹的平均抛撒子弹散布圆内均匀产生子弹的炸点(落点)。

1.4 毁伤判定及射击效力统计

1.4.1 子弹命中判定

子弹命中目标分2 种情况［1］:一是子弹直接命中目标;二是子弹威力触及目标。通过判断子弹实际落点与目标中心之距离是否小于目标等效圆半径来判断子弹是否直接命中目标。通过判断子弹落点与目标中心距离是否小于目标等效圆半径与子弹威力半径之和来判断子弹是否坐标毁伤目标。

1.4.2 目标毁伤判定及射击效力统计

目标毁伤的判定和解析法相同。比如:第j 个单位目标的等效圆半径为RTj，目标毁伤平均命中弹数ω=1，目标中心点的位置为(xTi，zTi)，子弹落点(炸点)的位置为(xi，zi)，只要满足条件:

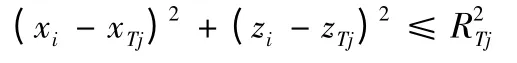
子弹就会命中且毁伤目标。如ω≠1，统计命中目标的子弹数，只要大于ω 则目标被毁伤。

或按照以下方法处理:在求得一发母弹所有子弹的落点坐标以后，即可依次判断n 发子弹是否落入第j 个单位目标等效圆内。若落入目标等效圆内，则子弹命中目标。若毁伤目标所需的平均命中弹数ω=2，故可产生一个0 ～1 的均匀随机数λ。当λ 属于0 ～1 的一个长为a =1/2 的区间内时，则认为目标被毁伤。不失为一般情况，取该区间为［0.3，0.8］，此时，RN(j)=1;否则RN(j)=0。

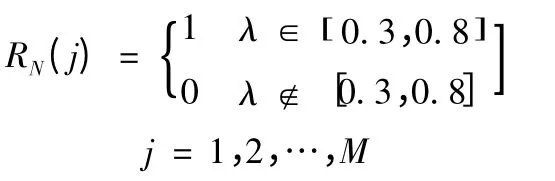
依据目标毁伤准则，根据以上仿真结果，判定目标毁伤情况，可求得一次齐射对目标的毁伤的数学期望［2-3］:

重复以上步骤，进行N0次模拟，得到模拟结果M1，M2，…，MN0

则毁伤比的数学期望:

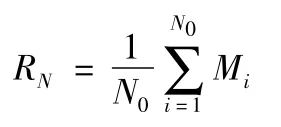
以此作为计算射击效力的指标。

2 初始计算条件

2.1 计算条件

远程火箭炮单炮对几种典型目标射击，假定一次齐射发射破甲杀伤双用途子母弹12 发，火箭炮每发母弹抛撒子弹数为600 枚，抛撒子弹散布圆平均半径为120 m，火箭炮决定诸元误差为0.3%D，散布误差为1/300D (D 为射距离)。

2.2 几种典型目标

幅员为500 m×500 m 的坦克连集结地域，坦克数量为10 辆，坦克在集结地域内均匀分布。瞄准位置为集结地域中央。多管火箭炮(MLRS)排阵地，配置数量为3 门，炮与炮间隔为250 m，分别呈三角形、一线配置，瞄准位置阵地中央。“帕拉丁”自行火炮排阵地，配置数量4 门，每2 门为一组，炮与炮间隔100 m，2 组之间间隔300 m，呈一线配置，瞄准位置为阵地中央。坦克连行进纵队，坦克数量10 辆，间距100 m，瞄准位置纵队中央。

3 仿真的实现

3.1 随机数的产生

随机数的产生是仿真计算的关键，而具有良好统计特性的随机数是获得可靠的仿真结论的主要保证。下面是2 类随机数的产生方法［4-5］。

3.1.1 均匀分布随机数的产生

下面使用的U(0，1)随机数采用素数模乘线性同余发生器PMMLCG 产生。其方法如下:设有一个整数序列Z1，Z2，…，Zn，定义

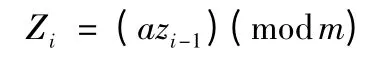
如果a 和m 满足条件:

1)m 为小于2b的最大素数。其中b 为计算机除符号位以外的字长。

2)a 为模m 的一个质元素。即在al-1 可以被m 整除的情况下，最小的整数为l=m-1。

则可以证明PMMLCG 具有满周期P=m。

对于32 位计算机，去掉符号位，则b=31，

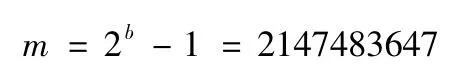
经过验证，性能比较好的PMMLCG 有:

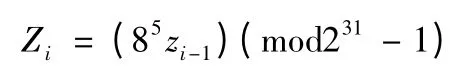
对上式进行归一化处理:

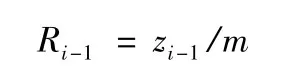
即可得到服从U(0，1)分布的随机数序列{Ri}。

3.1.2 正态分布随机数的产生

设r1和r2为2 个独立的均匀分布随机数，且服从U(0，1)作变换:

则η1和η2是2 个独立的N(0，1)随机数。由此可见，正态分布随机数的产生可归结为均匀分布随机数的产生。

3.2 子弹落点坐标的仿真实现

由射击误差的数学模型可知，第i 个子弹落点的坐标:

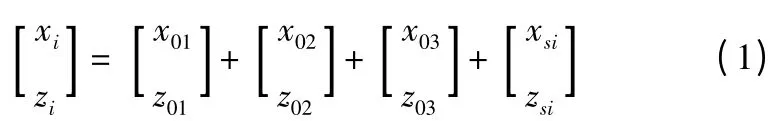
以σmx和σmz来产生正态随机数x0m，z0m(m =1，2，3)，并将子弹对落点中心的偏差作为xsi和zsi(i=1，2，…，600)。

若假定子母弹射击指向点与目标中心重合，则可求得一发母弹中所有子弹相对于目标中心的坐标:

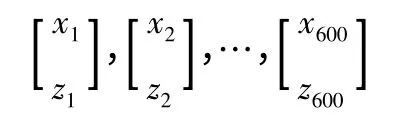
共有600 个坐标。远程火箭炮单炮一次齐射时，则应产生12 ×600 =7 200 个子弹坐标，此为一次仿真模拟的结果。

3.3 结果与分析

3.3.1 仿真结果

根据以上基本思路及情况设置，编程进行仿真(仿真模拟次数为2 000)的结果见表1。

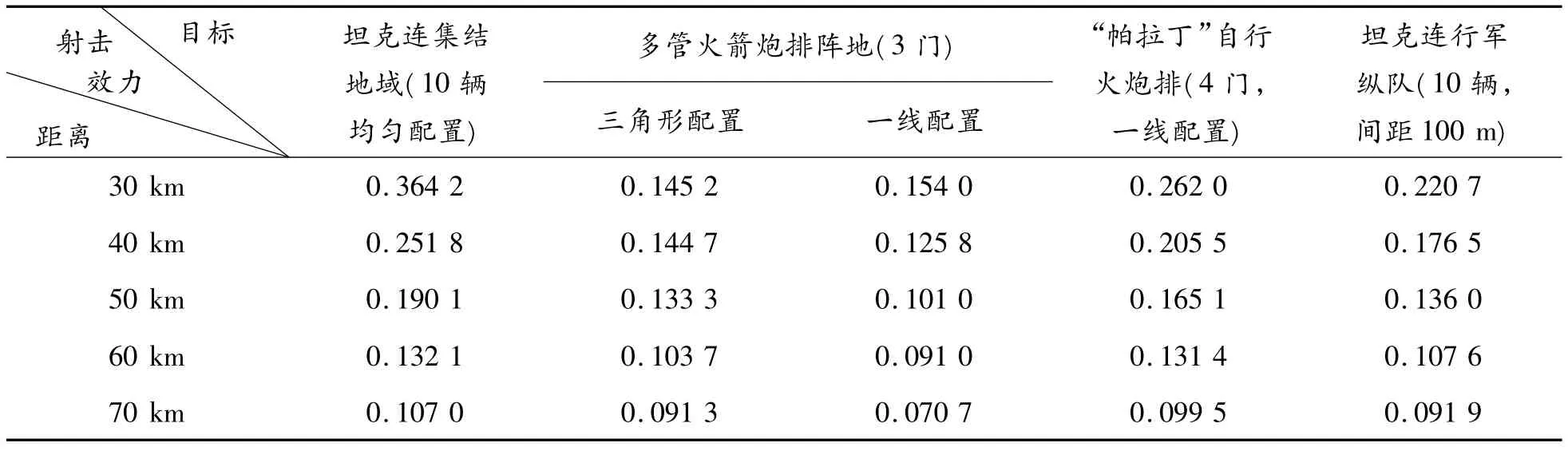
表1 单炮发射破甲杀伤双用途子母弹对典型目标射击，一次齐射的射击效力仿真结果

3.3.2 结论

根据计算机仿真模拟2 000 次的结果看，远程火箭炮单炮在常射距离上对上述4 种典型目标射击，一次齐射12 发破甲杀伤双用途子母弹，即可达到15%左右的毁伤。

按照文中的仿真算法，用两门远程火箭炮射击，两炮瞄准位置之间间隔为120 m(或选取适当位置)，各进行一次齐射，通过仿真试验，集结地域的坦克连、坦克连行进纵队和“帕拉丁”自行火炮都将有25%以上被毁伤。若用排(3 门炮)射击，经仿真计算，射击距离为50 km，对集结坦克连可达到35% 左右的毁伤;对MLRS 多管火箭炮排的毁伤在30%以上;对“帕拉丁”自行炮排射击可达到约40%的毁伤。由此可见，对上述几种典型目标射击时，参加射击的兵力应根据战术需要或作战任务，可选定1 ～2 门或排射击，在火力分配上应采取单炮分段射击的方式，以获得最佳射击效果。

［1］张廷良，陈立新.地地弹道式战术导弹效能分析［M］.北京:国防工业出版社，2001.

［2］靳树昌. 现代炮兵射击学［M］. 北京: 军事科学出版社，1999.

［3］许梅生.炮兵射击基本理论分析［M］.北京:兵器工业出版社，2004.

［4］靳树昌.远程火箭炮射击理论研究［M］.北京:海潮出版社，2005.

［5］程云门. 评定射击效率原理［M］. 北京: 解放军出版社，1986.