基于传统遗传算法的改进排爆机器人路径规划研究

王枫红， 邓志燕， 陈炽坤

（华南理工大学设计学院，广东 广州 510640）

路径规划技术是排爆机器人技术领域中的一个重要研究内容，要求机器人根据给予的指令及环境信息自主地决定路径，避开障碍物实现排爆任务。为了让排爆机器人在各种环境中能够及时的排除爆炸物，真正实现无人干预的自主式，对其进行路径规划算法的研究是非常重要的。

本文主要针对排爆机器人的全局路径规划方法进行研究，根据给定的工作环境信息条件，离线规划出符合某种给定规则的最优路径，即路径最短、能量最省等。

1 传统的路径规划算法和其存在的问题

路径规划技术经过几十年的发展，涌现出很多方法和思想。目前，比较成熟和被广泛接受的方法有：人工势场法、栅格法和遗传算法[1]。其中遗传算法因其编码技术和遗传操作比较简单，优化不受限制性条件的约束，故其应用最为广泛[2]。

但传统遗传算法具有如下缺点：编码不规范及编码存在表示的不准确性；单一的遗传算法编码不能全面地优化问题的约束表示出来[3]；传统遗传算法容易出现过早收敛；遗传算法通常的效率比其他传统的优化方法低[4]。

本文选择遗传算法对排爆机器人进行路径规划，针对传统遗传算法的一些缺点，对传统算法进行了一系列的改进，提出适宜的个体编码等。

2 基于传统遗传算法的改进算法

本算法主要从：判断路径、构造路径和最短路径三方面进行了探讨和研究，并对其进行模块处理，从而大大简化了排爆机器人的路径规划算法，便于算法维护，且能够及时的找到任意形状障碍物地图的最优路径。

2.1 判断路径

在本文的机器人路径规划中，目标是在一幅障碍物分布已知的二维地图上寻找一条最优路径使到达目标点距离尽可能短，同时尽可能少消耗机器人的能量。由于机器人本身有尺寸，先将障碍物的边界向外扩张半个机器人最大直径，将机器人当作一个质点[5]。若扩展之后的障碍物相交了，则没有有效路径，将相交障碍物合并为一个障碍物，如图1所示。采用凸多边形创建多个静止障碍物，就存在一个障碍物的有限集合S，S={S1, S2, S3,…Si}，其中：i为区域中的障碍物的个数。

2.2 构造路径

判断路径之后，我们则需要寻找排爆机器人的真正可行路径，也就是寻找机器人的可行区域。可视图法是目前最常用的构造路径方法。该方法虽然能保证在三维以下构形空间中求出最短安全路径，但是不能推广到更高维的空间中，且对于障碍物过多的时候，可视图比较复杂（如图2所示）时，采用该方法会导致可视图中有些线条是多余的，这样就减慢了路径规划的速度。为了提高路径规划速度，本文基于可视图的基本原理[6]，对其进行一系列改进寻找机器人可行区域的，构造新颖的可视图。

图1 障碍物的扩展

图2 利用可视图法创建的地图

首先生成常规的可视图如图2，对生成的连线按从短到长的顺序进行排序，生成一个由线段组成的队列。取第一条线段m，检查是否和其后的线段相交。如果发现队列中某一条线段n和线段m相交，那么从队列中删除n线段，以此类推，直到将所有队列中与线段m相交的线段删除。再取队列中m的下一条线段，重复上述步骤，直到取完所有的线段。图3所示为在图2基础上改进后所得到的新地图。

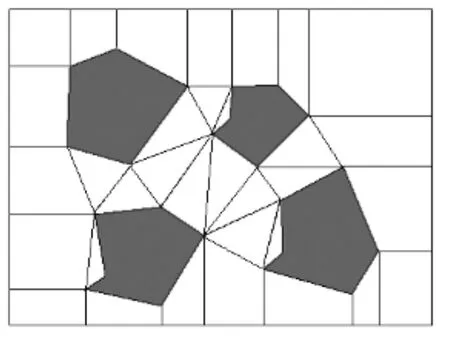
图3 改进的地图

可见此时机器人的可行区域就是由图3中的多边形组成。本算法把这些多边形当成单独的一个个区域，在进行最短路径搜索的时候针对的只是可行的多边形（非障碍物）。在进行个体编码时不采用常规二进制编码，而是对可行区域多边形边上的点进行编码，这样大大简化了遗传算法的个体编码，减少了路径规划的计算量。如图4所示为使用该算法产生的一条路径。

图4 新地图上产生的路径

2.3 最短路径

在找出机器人的可行区域之后，则需要在这个可行区域内找出最优路径。本算法基于传统遗传算法的优点，采用其进行最短路径的求取。为了让算法在很少的进化代数中就可以求出问题的最优解，且避免传统遗传算法的“早熟收敛”和“收敛速度慢”的问题，本文对传统遗传算法进行了如下的改进：路径个体编码没采用常规的二进制编码，而是采用多线段编码，大大简化了编码长度；结合排爆机器人的实际情况提出合适的适应度函数；对选择算子和变异算子进行改进，扩大种群的范围，避免快速进入局部最优解[7]。具体计算步骤如下：

1）路径的个体编码

本算法使用多段线表示路径，除了第1点和最后一点分别落在出发点和目标点上之外，其它路径线段与线段之间的连接点都必须落在地图连接线中点上，编码如图5所示。

图5 基因编码

基于上述编码原理，图4上的路径则可表示为((Xs, Ys), (X17, Y17), (X12, Y12), (X5,Y5),(X3, Y3), (Xg, Xg))，其中每个点的角标根据生成连接线按长度排序之后的位置，(Xi, Yi)代表是中间点的坐标，(Xs, Ys)和(Xg, Yg)分别表示起点和终点。

2）初始种群的产生

本算法中初始种群就是在地图的起点和终点确定，以及连接点生成之后，随机的选取这些连接点组成路径，如图6所示，是随机产生的路径。

图6 初始路径的生成

3）适应度函数

每条路径的优劣评价通过适应度函数来给出[8]。对于排爆机器人适应度的评价是行走路径的长短和能量消耗的大小，理想的状况是最短路径同时耗能最小。由于履带式排爆机器人的能量消耗主要取决于拐弯角度的大小和拐弯次数等因素，所以最短路径的情况下如果拐弯角度较大或拐弯次数较多都会增加能耗，其适应度不一定最好，所以最优路径是路径长短和能耗的最佳配合值。综上，排爆机器人的适应度函数确定如下：，其中：dist——对路

式中：xk——第k个连接点的x坐标。 (,, ,)gαn…μ是能耗函数，其能耗主要取决于拐弯半径、连接点数量以及地面的摩擦系数等因素。

4）改进后遗传算法的操作算子

（1）选择算子

为了增加群体的多样性，有效的避免早熟现象发生，本算法引入了相似度的概念。随机生成种群后，在遗传算法进行选择运算前，对群体中每两个个体逐位比较。如果两个个体在相对应的位置上存在着相同的字符（基因），则将相同字符数量定义为相似度R。在实验中设T=适应度平均值，在群体中取大于T的个体进行个体相似程度判断。R小的则表示这两个个体相似性差，当R≥L/2（L为个体的长度）时，即认为这两个个体相似[12]。

（2）交叉算子

采用单点交叉[9]。首先确定一个交叉概率，对选择后的子个体进行随机配对，然后为每一对个体产生一个[0, 1]的随机数，如果随机数小于交叉概率，则对该对个体随机指定的基因进行交叉操作。

（3）变异算子

变异是对群体中的元素（基因）加入随机扰动，变异与有节制地交叉一起使用，是一种防止过度成熟而丢失重要遗传信息的保险策略[10-11]。改进型变异算子优先选取和障碍物相交的线段的端点进行变异，同时限制变异所得的路点坐标在障碍物之外。并且对适应度值大的采用较少的变异率，适应度值小的采用较大的变异率。

（4）算法停止条件

利用多代之间的平均适应度之差小于某值Δ来终止[12]，本实验中Δ=0.5。

其算法的路径规划迭代步骤如图7所示。

3 算法的仿真分析

为了分析算法的路径规划效果，本文构造两种工作环境，它们所在的地图尺寸一样，不同的是障碍物的分布、密度以及形状，如图8所示，map1为障碍物稀疏地图，map2为障碍物密集地图。

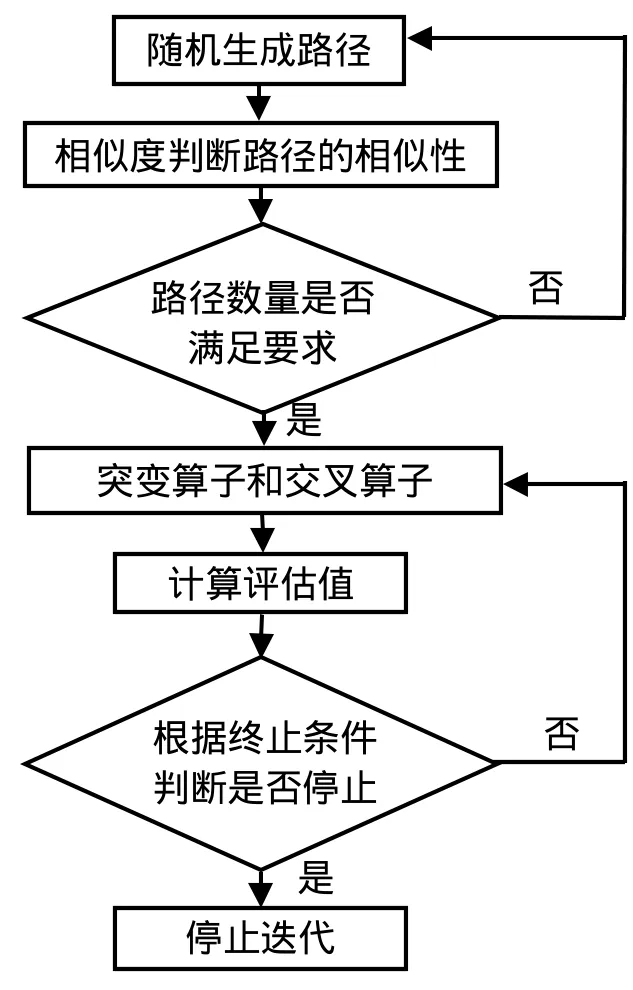
图7 基于传统遗传算法的改进算法流程图

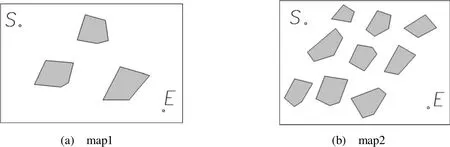
图8 环境地图

不同的种群大小，对收敛的代数和收敛的时间有很大的影响。群体的规模选取越大，获取的的路径越好，但收敛时间也越长；反之，群体规模越少，收敛时间越短，且有可能得不到最短路径。本实验对障碍稀疏分布的map1分别采用传统遗传算法和改进遗传算法对不同的种群做6次规划，得到的结果如表1所示。由此可见，相同种群大小的情况下，改进后的算法可较有效地缩短进化时间。

表1 不同种群下的进化结果比较

为了更明显的比较传统遗传算法和改进遗传算法在具体路径规划过程中的寻优效果，本实验取种群大小为30。比较map1中进化到20代的路径，map2进化30代的路径，仿真结果如图9、图10所示。

图9 分别使用GA和NGA方法第20代产生的路径

图10 分别使用GA与CGA方法第30代产生的路径

从图9和图10中可以很清晰看出，改进后的遗传算法有更好的寻优效果，优选的路径往往更加平缓，可使排爆机器人在距离相同的情况下能耗减少。

仿真实验证明，本文提出的算法较传统遗传算法能更快的找到较优路径，且应用此算法能够对任意形状的多边形进行路径规划，找出排爆机器人需求的路径。

4 结 论

本文针对传统遗传算法进化速度慢、容易陷入局部最优点等缺陷，提出了改进后新的路径规划算法。通过仿真实验验证了此算法的可行性，证实了该算法可以在一定程度上帮助排爆机器人更快的获得质量高的路径，减少能量消耗。

[1]高 巍, 赵 海, 罗桂兰, 等. 一种AAPF算法及其在多机器人路径规划中的应用[J]. 东北大学学报(自然科学版), 2009, (5): 644-647.

[2]唐 健, 史文中, 孟令奎. 基于遗传算法的时相关动态车辆路径规划模型[J]. 武汉大学学报(信息科学版), 2008, (8): 875-878.

[3]李 擎, 冯金玲, 柳延领, 等. 自适应遗传算法在移动机器人路径规划中的应用[J]. 北京科技大学学报,2008, (3): 316-323.

[4]周 巍, 李元宗. 基于改进遗传算法的煤矿探测机器人路径规划[J]. 太原理工大学学报, 2010, (4):364-367.

[5]Elshamli A. Mobile robots path planning optimization in static and dynamicenvironments [D]. The Faculty of Graduate Studies of The University ofGuelph, 2004.

[6]Beilingham J, Richards A, How J P. Receding horizon control of autonomous aerialvehicles[C]//Proceedings of American Control Conference Anchorage, AK,2002: 3741-3746.

[7]Ayala R V, Pecrez G A, Montecillo P F J, et a1. Path planning using genetic algorithms for mini-robotic tasks[C]//Hague Netherlands: IEEE SMC'2004 Conference Proceedings, 2004: 3746-3750.

[8]Qi Yuanqing, Sun Debao, Li Ning, et a1. Path plan for mobile robot using the particle swarm optimization with mutation operator [C]//Shanghai: Proceedings of the Third-International Conference on Machine Laming and Cybernetics, 2004: 2473-2478.

[9]Hu Yanrong, Rang S X. A knowledge based genetic algorithm for path planning of a mobile robot [C]//Proceedings of the 2004 IEEE International Conference on Robotics Automation, New Orleans,April, 2004: 4350-4355.

[10]Li Wei, Cassandras C G. A cooperative receding horizon controller for multivehiele uncertain environments [J]. IEEE Transactions 012 Automatic Control, 2006, 51(2): 242-257.

[11]杨姗姗, 戴学丰, 唱江华. 实现机器人动态路径规划的仿真系统[J]. 计算机工程与应用, 2009, 45(32):237-243.

[12]邓志燕, 陈炽坤. 基于改进遗传算法的移动机器人路径规划研究[J]. 机械设计与制造, 2010, (7):147-149.