离散点集最小包围圆算法分析与改进
李红军 , 张晓鹏
(1. 北京林业大学理学院,北京 100083;2. 中国科学院自动化研究所模式识别国家重点实验室&中法联合实验室,北京 100190)
平面点集的最小包围圆(smallest enclosing disk)问题的提出至少可以追溯至1857年[1]。只是随着计算机技术的快速发展,点集的最小包围圆应用越来越广泛,比如在工业机器人的设计、碰撞检测、机器学习、计算机图形学等领域中都有应用,研究成果也越来越多。仅就这个问题的算法设计而言,国内外也有不少文献。本文对这些现有的典型算法给予简单的介绍并进行分析和比较。为了避免重述,早期的研究结果可以参考Emo Welzl的有关工作[2]。1991年,Welzl在这篇文章中对早期的一些研究方法和结果进行了简要评述并提出了新方法。Welzl用随机增量算法求解平面点集的最小包围圆或椭圆( smallest enclosing ellipse ),并把这个算法推广到高维空间的最小包围球(smallest enclosing ball )、最小包围椭球(smallest enclosing ellipsoid )。后来的Mark de Berg等作了进一步的改进[3],我们称之为改进的随机增量算法。2005年,Frank Nielsen等也提出了一个基于对偶决策的、快速的、确定性算法[1],这里称之为对偶决策算法。2000年复旦大学汪卫等提出了一个离散点集最小包围圆的快速算法,我们称之为最远点优先渐近算法[4]。这3种算法思路清晰,不失为有代表性的经典算法。本文将对这3种算法进行分析、比较。
1 离散点集最小包围圆和典型算法
1.1 最小包围圆问题
问题:对于给定的平面上n个点所组成的一个集合P,求出P的最小包围圆,即包含P中所有点、半径最小的那个圆。也就是求出这个最小包围圆的圆心位置和半径。
对于这样的问题,为了便于理解各种算法,需要了解一些有关最小包围圆的性质:
性质 1 有限点集P的最小包围圆是唯一的。
这里约定,若P中只有一个点v,则最小包围圆是退化的,其半径为 0,圆心为点v。这个定理的详细证明参见文献[2]。
性质 2 非退化最小包围圆可以由 2个或者3个边界点定义。
显然,最小包围圆的构成有两种情况:第1种是距离最远的2个边界点定义了最小包围圆的直径。如图 1(a)所示,直径AB定义了这个最小包围圆,其余的点都是包含在这个圆的内部。这意味着不能仅仅通过求最大三角形的外接圆来计算最小包围圆。第2种情况是最小包围圆的边界上有3个以上的点,则任意3个边界点为三角形顶点所定义的外接圆确定了这个点集的最小包围圆。如图 1(b) 所示,这个最小包围圆由边界点 A、B、C所形成的三角形的外接圆定义。需要注意的是,边界线上可以有3个以上的点,只是任意3个边界点定义的外接圆是相同的。因此,求点集P的最小包围圆等价于求这些边界点的最小包围圆。

图1 最小包围圆由2个或3个边界点确定
性质 3 点集P中,距离最大的2个点A、B不一定都在边界上,但是必有,这里d为点集P的最小包围圆的长度。
如图2所示,点集P的最小包围圆由等边三角形ABC所定义,但是线段AD却是最大的边。显然,线段AD为直径的圆小于点集P的最小包围圆。
证明见文献[3]。

图2 最长线段不一定是最小包围圆直径
性质 4 直角三角形或钝角三角形的3个顶点的最小包围圆是以最长边为直径的圆;锐角三角形3个顶点的最小包围圆是三角形的外接圆。
证明:(1)设直角三角形或钝角三角形ABC的最大边为AB,则A、B两点确定的最小包围圆是以AB为直径的圆,则点C在圆上或者圆内,如图3(a)所示。根据引理1的前一部分知,A、B、C 3点确定的最小包围圆还是以AB为直径的圆。
(2)对于锐角三角形ABC,由于点C不属于以AB为直径的圆,因此,根据引理1的后一部分知点C在A、B、C三点确定的最小包围圆DABC的边界上;同理B和C也在最小包围圆DABC的边界上。不共线3点确定1个圆,所以DABC是A、B、C的外接圆,见图3(b)。
上述性质对于理解、构造或者实现最小包围圆算法有一定帮助。下面对几个常用的、经典的算法思想进行简要介绍和分析。
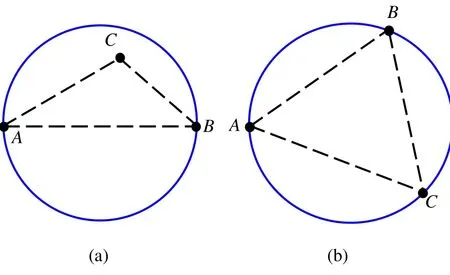
图3 不共线三点确定的最小包围圆
1.2 改进的随机增量算法
Mark de Berg曾给出一种比较典型易于理解的随机增量算法(randomized incremental algorithm, 简记为 RIA)[3]。 其主要思想是:第一,随机打乱点集中所有点的顺序;第二,以序列中前2个点构造最小包围圆D;第三,依次搜索其余的点,若某个点v在D外,则重新构造最小包围圆D',使D'饱含D中的所有点且以v为边界点。重复执行第3步,直到求出最小包围圆。
这个算法的关键在于第3步,以v作为边界点构造最小包围圆,从而增加了构造约束,减少了自由度。该算法的内存耗用少,速度快。在随机点集的条件下,期望运行时间为O(n)。但是,若原始输入序列是有序的,则打乱点集的顺序也是需要耗费时间的。
1.3 最远点优先渐近算法
2000年汪卫等提出一种准确且快速的点集最小包围圆算法[4],即最远点优先渐近算法,简记为DFAA。该算法的主要步骤是:第一,在点集中任取3个点:A、B、C;第二,以这3个点构造最小包围圆D;第三,在点集P中查询距离D的圆心最远的点v;若v在D内则算法终止;否则,第四,在{A,B,C,v}中选取3个点,构造包含这4个点的最小包围圆D',转第二步骤,其中选取的这3个点尽可能是边界上的点。
该算法实际上是一个确定性算法。主要的困难和时间耗费在第四步。事实上,根据引理1,这一步是可以改进的,因为新加入的点v必定是新的最小圆的边界点。于是这一步可以修改为:
以 v为边界点,并在{ A,B,C }中选取 2个点,构造包含这4个点的最小包围圆D',转第二步骤,其中选取的这3个点尽可能是边界上的点。
修改后的算法判断会减少,从而加快运行时间。第 3节的数值实验以修改后的算法(记为DFAA+)作为对比。该算法的时间复杂度为中R是所求的最小圆的半径,d为点集中不在圆周上但距圆周最近的点到圆周的距离。实际应用中,该算法时间复杂度是线性级的。
1.4 对偶决策算法
2005年Frank Nielsen提出一个快速近似的最小包围圆算法[1],这个算法通过求解一系列的对偶决策问题(dual piercing Decision Problems)来实现,简记为DPs。该算法的主要思想是:第一,计算所有点在x轴上的投影区间[min x, max x];第二,计算所有点到第1个点的距离最大值d1;第三,以4为初始半径,以 ε =8为误差控制,搜索区间为[maxx- r, minx+r]构造对偶决策,并进行迭代求解。其中,ε0为用户指定的误差控制阈值。
该算法优点是不但能够求出平面上点集的最小包围圆,也能求出圆盘集的最小包围圆。算法时间复杂度为,其中ε为最小包围圆的误差控制阈值,即该算法是一个近似算法。该算法的速度较快,也属于线性阶的,此外,算法基本属于确定性算法,其最坏时间复杂性比平均时间复杂性略差。但是该算法设计比较复杂,内存耗用比上述两种算法大。
上面这3个常用算法以随机增量算法影响比较大,我们的算法主要是对这个随机增量算法进行改进,使其成为确定性算法,并加快求解时间。
2 较远点对定义初始包围圆的增量算法
文献[3]介绍的随机增量算法试图通过生成点集的随机顺序来避免最坏时间复杂性,从而优化求解过程。事实上,这个目的可以通过调整距离较远的 2个点作为输入的前 2个点而得以解决。之所以不用相距最远的2个点,是因为求解相距最远的点对比较耗时。我们改进算法的主要步骤是:
Step 1 计算点集P的轴定向包围盒,并记录分别属于不同边的4个边界点,设为,,如图4所示。轴定向包围盒的边界点或许超过4个,为了减少算法比较和内存耗用,每条边记录1个边界点。

图4 计算点集的包围盒信息
Step 2 计算这个轴定向包围盒的宽(Bw)和高(Bh)。
Step 4 构造包含p1,p2的最小圆。之后的步骤用第1.2节介绍的改进的随机增量算法。
根据性质3易知,p1,p2确定的最小包围圆是整个点集的最小包围圆的子集。从这 4步 可以看出,本文的改进算法是对改进的随机增量算法的初始包围圆进行了特定的初始化,使得初始包围圆比较大,而计算这种轴定向包围盒的时间复杂度是O(n)的,因而迭代次数减少,计算时间减少。更重要的是,这样可以避免点集的最坏输入顺序,也不需要对输入点集生成随机顺序。我们把这个算法称为较远点对定义初始包围圆的增量算法, 简记为FIIA。
3 实 验
数值验证实验是在个人台式电脑上进行。电脑的主要配置是:Intel(R) Core(TM)2 Extreme,CPU X9650@3.0GHz, 内存为3.0G。
为了对比本文分析的3个经典算法和本文的改进算法,设计了4组数据:矩形域随机点集、圆域随机点集、共线随机点集和共线有序点集。其中,前2个数据为二维区域随机点集。
矩形域随机点集的采样区域为

采样点选取为此区域内的服从均匀分布的随机数对。
圆域的随机点集采样区域为

共线随机点集和共线有序点集都是来自于直线上的点,直线方程为

其中,本次实验的参数k=0.4。这2个点集的差别在于共线随机点集的点序是随机的,而共线有序点集是按照x坐标递增采样。相邻2个采样点之间的间隔引入随机数。这4个数据的采样点个数和求取最小包围圆的平均实验时间列在表1。其中平均实验时间为实验重复进行 50次的平均运行时间。表1中的RIA表示改进的随机增量算法(见第1.2节), DFAA+为改进第四步后的最远点优先渐进算法(见第1.3节),DPs表示对偶决策近似算法(见第1.4节), FIIA为本文提出的较远点对定义初始包围圆的增量算法(见第2节)。表
1中各个数据的最优时间用加粗的字表示。从表1可以看出,在本文罗列的3种经典算法中,在对偶决策近似算法(DPs)时间开销最大。最远点优先渐进算法(DFAA+)最好。本文较远点对定义初始包围圆的增量算法(FIIA)是对随机增量算法(RIA)的改进,时间效率大大提高,尤其是点集为共线的情况下,效果更加显著。

表1 实验数据信息和平均运行时间
实验数据的截图如图5所示,因为4个算法算出的圆心和半径相同,故实验结果的截图相同,因而也说明各个算法的正确性。

图5 实验数据及其最小包围圆
实验中最小包围圆的空间扩展过程也可以显示不同方法的收敛速度。这里我们把RIA算法和我们的FIIA算法进行对比,如图6所示。图6中的实验包含 50个随机点,每个子图下方的数字表示前k个点确定的最小包围圆。图6中的第1行3个图显示RIA算法的最小包围圆的动态扩展过程,第2行是我们的FIIA算法的运行结果。

图6 RIA和FIIA算法前k个点确定的最小包围圆, (a)-(c)为RIA算法结果;(d)-(e)为FIIA算法结果。
对比2行的k值可以看出,RIA算法在前41个点时可以求得最小包围圆。而我们的 FIIA算法,由于预处理中选取了距离较大的2个点作为前2个输入点,因此收敛速度快很多,算法在计算到前 22个点时就求得了最小包围圆。可见,我们的改进算法在收敛速度方面有明显的优势。
4 结 论
关于离散点集的最小包围圆问题,本文首先概述了点集最小包围圆的几个主要性质,这对于理解或构造最小包围圆算法有直接的影响。接着本文对随机增量算法、最远点优先渐近算法、对偶决策算法等当前比较常用、比较典型的算法进行分析和对比实验,结果表明过去的这3种算法中,汪卫等 2000年构造的最远点优先渐近算法在时间效率方面最高。其间我们对最远点优先渐近算法进行了细微的改进,减少了枚举次数。
本文主要对随机增量算法改进,即用轴定向包围盒边界上的较远点对,作为随机点集序列的前两个元素,实现随机增量算法的输入点顺序的优化。基于这一改进,本文提出的这个算法称为较远点对定义初始包围圆的增量算法(FIIA)。我们的这个新算法是确定性算法,不再需要对点集的顺序进行随机化处理,并且求取最小包围圆的速度显著提高。在工程实践中,点集的轴向包围盒往往在读入数据时就已经算好,因此,其结果能直接取代本算法的前两步骤而获得更好的时间性能。
[1]Frank N, Richard N. A fast deterministic smallest enclosing disk approximation algorithm [J].Information Processing Letters, 2005, 93(6): 263-268.
[2]Emo W. Smallest enclosing disks (balls and ellipsoids)[C]// Maurer H. (Ed.), New Results and New Trends in Computer Science, Lecture Notes in Computer Science, Heidelberg: Springer-Verlag,1991: 359-37.
[3][荷兰]Mark de Berg, Marc van Kreveld, Mark Overmars, et al. 计算几何: 算法与应用(第2版)[M].邓俊辉译. 北京: 清华大学出版社, 2005: 99-103.
[4]汪 卫, 王文平, 汪嘉业. 求一个包含点集所有点的最小圆的算法[J]. 软件学报, 2000, 11(9):1237-1240.

