高精度自适应的四边形网格重建

刘 丽 ， 吕 雪， 伯彭波

（1. 山东师范大学信息科学与工程学院，山东 济南 250014；2. 山东省分布式计算机软件新技术重点实验室，山东 济南 250014；3. 香港大学计算机科学系，香港）

随着计算机辅助设计与制造技术的迅速发展，逆向工程技术在工业领域得到越来越广泛的应用。逆向工程技术在对已有的机械零部件进行复制，特别是在引进产品的国产化和备品备件的制作方面都有重要意义。海量数据点集的重构方法很多[1-6]，其中网格曲面作为一种曲面表示形式由于具有简单、统一的优点，已经成为重要的曲面表示方法。

Hoppe[7]提出通过采样点的局部信息自动计算各点处的法向信息，利用切平面线性逼近待重建曲面的局部模型，建立离散点集的距离场函数，然后用等值面抽取的MC算法得到三角片逼近曲面。Amenta[8]通过构造采样点集的三维Voronoi图，利用Delaunay三角化方法来重建网格曲面。Bradley[9]提出了一种依赖种子点增长的网格曲面重建算法。从选定的种子点开始，通过后选点与当前网格的可见关系来判断该点是否在网格上以及确定它的连接关系，最终获得一张或多张网格曲面。Floater[10]提出了无网格参数化的曲面重建算法。首先将原点初始数据点集投影到平面上，运用平面Delaunay三角化方法将投影点集分割成若干三角形，从而得到点集的连接关系，最后通过映射点集的连接关系确定初始点集的拓扑连接。

上述算法都是基于三角形网格，为提高有限元分析的精度，出现了四边形网格的曲面重建。最简单的四边形网格曲面重建算法就是将相邻对三角形结合成一个四边形，三角形结合的顺序影响网格的质量。Lee等[11-13]就三角形结合顺序给出了几个启发式的步骤，生成了四边形占优的网格，减少孤立三角形的数量。这种方法的缺点是存在不规则节点，不能保证单元沿边界排列。Zhu[14]利用波前法生成四边形网格，首先在边界产生初始节点，再利用波前生成三角形网格，然后合并三角形生成四边形网格。Blacker和Roger等人[15]提出了一种生成四边形网格的Paving方法，由外向内生成成排的单元，在特殊区域进行相交判断。但是只能解决边界点为偶数的有限元网格重建问题。

海量数据点集的网格重建方法中常用的主要衡量标准：降噪和剔除离群点；保持物体原状，特别是尖锐特征；封闭的网格拓扑；根据表面的复杂程度自适应调节网格分布；网格尽量满足最优原则。根据这些原则，本文提出了一种新的四边形网格重建算法，不仅能够满足上述网格重建标准，而且可以根据精度要求调整网格密度。

1 相关定义及说明

定义1 数据点集S内任意数据点pi，都存在另外数据点pj，使成立，则称数据点集S的采样密度为δ。如果采样密度为δ的数据点集中存在半径大于δ的球体内没有数据点，则认为该区域为空洞。

为了保证拓扑结构正确，体现数据点集的空洞，定义立方体边长size的取值范围为

1.1 定义

边长size必须控制在一定范围内，这是因为如果立方体边长size过小，相邻数据点可能被划分在不相邻的立方体内；反之，如果边长size过大，不同区域的数据点，甚至之间存在空洞的数据点可能被划分在相邻或同一个立方体内。根据网格的生成规则，前一种情况中的重建网格不连续，后一种情况中的重建网格把空洞给填充，改变了数据点集的拓扑结构。

定义 2 曲面上某点的高斯曲率为该点两个主曲率的乘积，反映了曲面局部的弯曲程度。四边形网格顶点的离散高斯曲率求解，利用离散微分几何，由直接相连的网格顶点构成的三角网格估计（如图1），忽略对角顶点对其曲率的影响。

图1 网格顶点的离散曲率

其中，A表示顶点pi所在三角形面积的和，n-1表示顶点pi所在三角形的个数。当jα为锐角时，

当jα为钝角时

1）面片抽取的最小环原则 在网格中以顶点vi开始，沿着多边形网格的边vivj寻找到下一个顶点vj，重复迭代该过程，直到回到顶点vi为止。此时，封闭顶点形成的多边形即为抽取面片。从顶点vi开始再回到顶点vi的封闭路径很多，这些封闭路径形成的面片顶点存在包含关系，寻找最小顶点集合的封闭路径。

1.2 部分原则

点集S′⊂S，这就是最小环原则。在面片抽取过程中遵循最小环原则，保证多边形面片中不能再抽取出边数更少的面片，消除面片重叠。

2）局部细分原则 如果网格顶点pi的离散高斯曲率 k ＞εsub，对共享该点的面片进行局部细分。需要注意的是尖点及折叠边上的顶点即使经过多次细分，曲率变化仍然不是很大，这可能造成细分无限延续，因此定义共享顶点pi的网格进行局部细分的条件为：第一，细分次数不大于4；第二，顶点的离散曲率 k ＞εsub。

对共享顶点pi的面片 fi细分，新顶点vi表示如下

其中，n表示面片 fi的顶点数。细分顶点vi与面片 fi中各个顶点相连生成三角形面片，删除共享顶点pi的相邻面片 fi,fj的公共边，如图2所示。

图2 面片的局部细分

均匀划分海量数据点集的最小包围盒，重建网格的密度较为均匀，不能充分体现细节特征。通过对多边形网格进行自适应的局部细分，增加弯曲程度较大区域的网格密度。

3）整体细分原则 为使多边形网格转化为四边形网格，对多边形网格做整体细分。其中，网格顶点保持不变，新面点vface和新边点vedge的计算如下：

（1）设面片 f中的网格顶点为 v1, v2,…,vn，则相应的新面点为

（2）设相邻面片 fi,fj的新面点为vfacei，vfacej，公共边端点为v1,v2，则相应的新边点为

（3）设边界边的两端点为v1,v2，则相应的新边点为

将新面点与周围的新边点相连，建立新的拓扑结构，得到海量数据点集的四边形重建网格。

2 算法实现

2.1 算法流程

算法采用八叉树空间分割的结构，使得对于点的搜索无须遍历整个点集，只要在当前立方体区域及其邻域查找，节省了搜寻时间。

步骤1 均匀分割与坐标轴平行的最小包围盒，得到l×m× n个边长为size的立方体。设包围盒沿X,Y,Z轴方向的最小坐标为,，最大坐标为，则立方体（i,j,k为立方体沿X,Y,Z轴方向的索引号）表示为

步骤2 简化立方体Bi,j,k内的数据点集，按一定规则连接相邻立方体内的简化点，生成多边形网格。计算网格顶点的离散高斯曲率，删除顶点离散曲率 k ＜εdel且删除该点形成的新网格的边数小于等于6的顶点（对于边数大于6的网格认为是空洞，不予处理）。

步骤3 按照最小环原则从步骤2中的网格中抽取多边形面片，计算网格顶点的离散高斯曲率，对满足局部细分条件的多边形面片进行局部细分。

步骤4 对步骤3中的多边形面片进行整体细分，使之全部转化为四边形面片，并对四边形面片进行优化，分裂度较大的网格顶点。

2.2 算法拓展

1）数据简化

在海量数据点集的重建过程中，大量的数据点不利于存储、操作以及重建，严重影响重建算法的效率，因此对数据点集进行简化。此外，通过对数据点集的简化，减少了采样噪音对重建网格的影响。

简化立方体内数据点的方法主要有：第一，每个立方体内离中心最近的数据点作为简化点，这种方法的好处是重建网格大致均匀，缺点是没有充分考虑立方体内数据点的分布，如图3(a)所示；第二，每个立方体内数据点的平均值点作为简化点，这种方法虽然考虑了数据点的分布情况，但重建网格往往不均匀，如图3(b)所示。为了更好地体现立方体内数据点集的分布，且使网格形状较为均匀，定义简化点Vi,j,k为

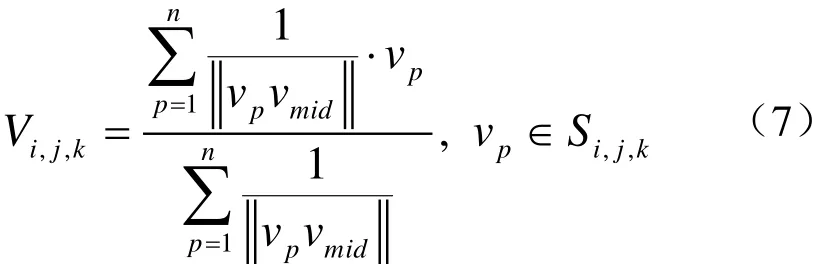
图3 数据点简化的3种方法

2）网格生成

连接立方体内的简化点生成多边形网格，连接规则如下：如果与立方体V面相邻的立方体Vface内有数据点集，则把V内的简化点与Vface内的简化点相连；否则如果与立方体V边相邻且与立方体Vface面相邻的立方体Vedge内有数据点，则把V内的简化点与Vedge内的简化点相连。

相邻立方体内数据点连接的优先级为面相邻的优先级大于边相邻的优先级。重建网格中大多数为四边形，此外还包含了少许的三角形网格、五边形网格和六边形网格，以及其他形状的网格。在这里至多考虑六边形网格，对于边数大于六边形的网格区域认为是空洞，不予处理。

由于数据点集自身拓扑结构的复杂，以及扫描过程中的误差等原因，重建网格可能会出现悬面（如图4(a)）和悬边（如图4(b)）。产生的悬面无法判断是否是扫描物体本身的形状，因此予以保留。但是，悬边是不允许出现的，若某个顶点只有一条边与之相连，则删除该顶点及其相连的边，保证重建网格拓扑结构正确。

图4 悬面和悬边

3）网格优化

根据生成多边形网格的连接规则，每个简化点至多和它周围6个数据点相连。定义网格中顶点v的度是和v相关联的边的数目，则多边形网格顶点的度最多为6。在网格局部细分的过程中，每细分一次，部分网格顶点的度增加1，限制网格局部细分的次数不大于4，则网格顶点的度至多为10。对多边形网格进行整体细分，原网格顶点的度不变，三角形、四边形、五边形和六边形面片的新细分顶点的度分别为3，4，5，6，因此整个四边形网格顶点的最大度为10。

顶点度过大会在顶点周围产生质量较差的网格，为改善这些局部区域的网格质量，减少顶点的度，在算法中引入拓扑优化操作，将度较大的顶点分裂为两个新顶点。度为nc的网格顶点c，与顶点c相连的顶点a，从顶点a沿顺时针，将顶点c的网格分成两部分M 和N（如图5）。分裂网格顶点c，生成新的顶点d, e，连接顶点a, b, d, e生成新的四边形网格。顶点c分裂后，新网格顶点的度为

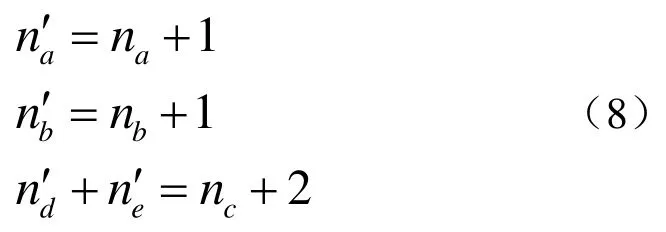
网格顶点d, e分别在区域M, N内，位置由所在区域的多边形网格决定

其中，m,n分别为区域M,N内共享顶点c的四边形网格的个数，pi为四边形网格的质心。分裂重建的四边形网格中度较大的顶点，使顶点的度都不大于6（如表1），改善局部区域的网格质量。

图5 顶点分裂

表1 分裂网格顶点度的变化

3 应用实例

下列是对文物扫描数据点集进行四边形网格重建的例子，扫描数据点只有位置信息。图6全景式地说明了四边形网格生成的主要步骤，其中数据点集的个数为210963个。

图7～图9是图中数据点集重构的例子。图7中立方体边长size适合的范围为9.2～17.5。图7(b)中相邻数据点被分割在包围盒中不相邻的立方体内，连接规则只连接相邻数据点，因此重构的四边形网格不连续。图7(c)是罐子的罐口，由于立方体边长size过大，罐口的数据点被分割在包围盒中相邻的立方体内，根据连接规则这些数据点相连生成新边，将罐口的空洞部分封闭起来，导致拓扑结果错误。

图8(a)中数据点集的个数为96847个，图8(b),(c)是图 8(a)中数据点集的不同分辨率的重构网格。图9(a)中数据点的个数为298353个，图9(b)是图9(a)中数据点集的重构网格。

图6 海量数据点集网格重构的主要步骤

图7 网格重建实验结果之一

图8 网格重建实验结果之二

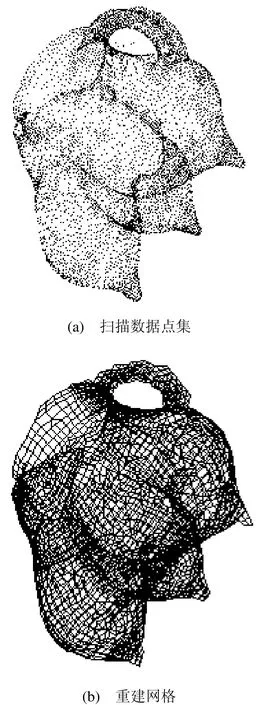
图9 网格重建实验结果之三

通过对实例中重构网格的分析可知，立方体边长size在式(1)的范围内，对复杂拓扑的海量数据点集，本文算法都可以重建出拓扑结构正量数据点集，本文算法都可以重建出拓扑结构正确、细节特征明显的多分辨率网格。另外，在实验中发现，采样数据点越均匀，重建的四边形网格质量越好。

4 结 论

本文提出的海量数据点集的四边形网格重建算法，只需给出物体表面数据点的位置信息，不需要法向、曲面边界等附加信息，就可以重建出复杂拓扑的四边形网格。本文算法具有提高重建网格精度，降低构造曲面片难度等优点，有较大的实用价值。今后的工作主要是实现多视图、多基点、变分辨率测量数据的坐标归一化，以及根据重建网格构造C1连续的曲面片。

[1]Kazhdan M. Reconstruction of solid models from oriented point sets [M]. Eurographics Symposium on Geometry Processing, 2005: 73-82.

[2]Zhao H, Osher S, Fedkiw R. Fast surface reconstruction using the level set method [C]//1st IEEE Workshop on Variational and Level Set Methods, 2001: 194-202.

[3]Doi A, Fujiwara S, Matsuda K, et al. 3D Volume extraction and mesh generation using energy minimization techniques [C]//1st IEEE International Symposium on 3D Data Procession Visualization and Transmission, 2002: 83-86.

[4]Lin Hongwei, Tai Chiewlan, Wang Guojin. A mesh reconstruction algorithm driven by an intrinsic property of a point cloud [J]. Computer-Aided Design,2004, 36(1): 1-9.

[5]Sergei A, Anath F. Efficient surface reconstruction method for distributed CAD [J]. Computer Aided Design, 2004, 36(2): 799-808.

[6]Habbib A, Warren J. Edge and vertex insertion for a class of C1 subdivision surfaces [J]. Computer Aided Geometry, 2004, 16(4): 223-247.

[7]Hoppe H, DeRose T, Duchamp T, et al. Surface reconstruction from unorganized points [J]. Computer Graphics, 1992, 26(2): 71-76.

[8]Amenta N, Bern M, Kamvysselis M. A new Voronoi-based surface reconstruction algorithm [C]//Proc of ACM SIGGRAPH’98. Orlando, 1998: 415-421.

[9]Bradley C. Rapid prototyping models generated from machine vision data [J]. Computers in Industry, 2001,41: 159-173.

[10]Floater M S, Riemers M. Meshless parameterization and surface reconstruction [J]. Computer Aided Geometric Design, 2001, 18(3): 77-92.

[11]Lo S H. Generating quadrilateral elements on plane and over curved surfaces [J]. Computers and Structures, 1989, 31(3): 421-426.

[12]Bruce P, John M, Andrew K. Automatic conversion of triangular finite element meshes to quadrilateral elements [J]. International Journal for Numerical Methods in Engineering, 1991, 31: 67-84.

[13]Lee C K, Lo S H. A new scheme for the generation of a graded quadrilateral mesh [J]. Computers and Structures, 1994, 52: 847-857.

[14]Zhu J Z, Zienkiewiez O C. A new approach to the development of automatic quadrilateral mesh generation [J]. International Journal for Numerical Methods in Engineering, 1991, 32: 849-866.

[15]Blacker D. Michael B. Paving: a new approach to automated quadrilateral mesh generation [J].International Journal for Numerical Methods in Engineering, 1991, 32: 811-847.