晶闸管可控电抗器的谐波产生特性研究

孙媛媛 尹志明 郑伟杰 刘 颖

（1.山东大学电气工程学院 济南 250061 2.中国电力科学研究院 北京 100192 3.山东电力集团济南供电公司 济南 250021）

1 引言

晶闸管可控电抗器（Thyrisor Controlled Reactors，TCRs）由两个反并联的晶闸管串联一个电抗器组成，它是静止无功补偿中的重要组成元件[1]。TCRs作为可变电感，可快速、平滑地调节所吸收的无功功率，因此它和晶闸管投切电容器（Thyristor Switched Capacitor,TSC）一起成为电力系统中无功补偿和电压调节的重要手段[2,3]。然而，从电能质量方面考虑，TCRs 作为开关型电力电子器件，在运行过程中，将大量的谐波电流注入系统，是电力系统中重要的非线性谐波源[4,5]。

分析 TCRs 产生的谐波，主要有四类方法。①恒流源法：基于TCRs的典型谐波频谱和特定运行工况的基波潮流结果，根据恒流源法的公式计算得出TCRs 注入系统的谐波电流[6-8]，该方法在目前的谐波分析中应用广泛。②诺顿等效电路模型：在恒流源模型的基础上并联表征TCRs 谐波电压和谐波电流自耦合效应的导纳[9,10]，但未考虑谐波电压和谐波电流之间的互耦合作用。③基于传递函数的模型：TCRs 中背靠背的晶闸管交替导通和关断，任一晶闸管导通时定义开关函数为1，所有晶闸管都关断时定义开关函数为0[11-13]；基于此传递函数，在频域中推导得出TCRs的谐波模型[14]。该模型通过两个导纳矩阵将TCRs 各次谐波电压和谐波电流的耦合关系展示出来，模型准确但计算复杂。④时域法：用微分方程描述TCRs 电压和电流之间的关系，通过求解微分方程得出TCRs 注入系统的谐波电流[15]。该方法准确，但对大系统来说，搭建模型所需的工作量大且仿真运行时间长。

以上各谐波模型的提出均以在谐波潮流中应用为主，缺乏对TCRs 谐波特性的分析。而研究TCRs的谐波产生特性，将有助于对谐波源建模采取合理的近似和简化以及谐波潮流分析的进行。频域中TCRs的谐波矩阵模型[14]通过完全解析的公式将TCRs 端口各次谐波电压和谐波电流之间的耦合关系直观地展示出来。本文将基于TCRs的谐波耦合矩阵模型，对TCRs的谐波产生特性进行深入分析。研究发现，TCRs的每次谐波电流均由三部分组成：由基波电压产生、由同次谐波电压产生以及由不同次谐波电压的耦合作用产生的谐波电流。本文首先分析了谐波电流各组成部分的贡献大小，在此基础上提出了TCRs的忽略谐波电压共轭影响的模型、解耦的模型和恒流源模型，给出了各简化模型的解析计算公式，并研究了触发延迟角对简化模型精度的影响。

2 TCRs的谐波耦合矩阵模型

TCRs 多按三角形联结方式在三相电路中使用，如图1 所示。3 及3的倍数次谐波经三相电感环流而不注入交流系统。

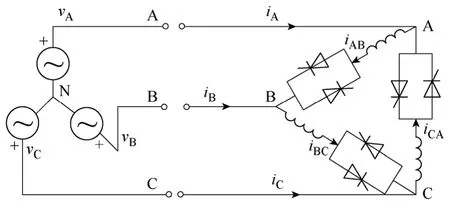
图1 三相三角形联结TCRs的电路图Fig.1 Circuit of three phase delta connection TCRs

根据三相TCRs的工作原理和传递函数，可在频域中推导出其谐波耦合矩阵模型[14]

式中，h=1,5,7,…,H，H为所计算的谐波最高次数，和分别为TCRs 端口的h次谐波电流和电压相量，为的共轭分量，Y+和Y-是TCRs的谐波耦合矩阵模型。矩阵各元素的解析表达式为

式中，α为晶闸管的触发延迟角；L为TCRs 中的电抗值。

模型表明，TCRs的谐波电流不仅由其端口的谐波电压产生，而且也与其谐波电压共轭分量有关。该模型将TCRs 端口的谐波电压和它所产生的谐波电流之间的耦合关系通过Y+和Y-两矩阵直观地体现出来，且矩阵的各元素以完全解析的公式给出。通过分析谐波耦合矩阵元素的特点，可对TCRs的谐波产生机制进行分析。

3 TCRs的谐波耦合矩阵特性分析

首先给出Y+、Y-各元素相对大小的直观比较（见图 2，触发延迟角为 20°）。所有元素均以（幅值最大的元素）为基准进行标幺化，对比结 果以百分比的形式给出。由图可知，Y+的对角线元素、第一行、第一列以及Y-的第一行元素有较大的幅值，说明这些元素所对应的电压分量在TCRs的谐波电流产生中起主要作用。

3.1 基波电压的作用

Y+、Y-的第一列元素共同表征了TCRs 端电压的基波分量对TCRs 各次谐波电流产生的影响。因Y-的第一列元素为零，该影响完全由Y+的第一列元 素决定。由式（2）可知，的幅值有如下形式：

式中，sin ［(h+1)α］的取值在（0,1）的范围内；的幅值随谐波电流次数h的增大，以的速度递减。如果供电电源中不含谐波，TCRs 产生的谐波电流随谐波次数减小的速度将大于整流装置[13]。

由式（3）可知，任一元素幅值均是触发延迟角的函数，图3 示出了随触发延迟角和谐波次数的变化规律（所有元素均以为基准进行标幺化）。这一列元素不含任何谐波的作用，是恒流源模型的解析计算公式。因此可将式（1）所示的完整模型分为基波电压（恒流源模型，）与谐波电压的作用两部分，如式（4）所示。

图2 Y+、Y -矩阵元素幅值相对大小对比图（触发延迟角20°）Fig.2 Elements relative amplitude comparison for Y+and Y-when the firing angle is 20°

图3 Y+矩阵第一列元素幅值随触发延迟角的变化规律Fig.3 The amplitude variation of Y+first column elements with firing angle

3.2 谐波电压对基波电流的作用

TCRs的基波电流主要由基波电压通过1,1Y+产生（1,1Y+即为TCRs 基频下的等效导纳），但Y+和Y-的第一行均有非零元素，表明TCRs 将供电端的部分谐波电压转化为基波电流送入系统。元素的幅值为

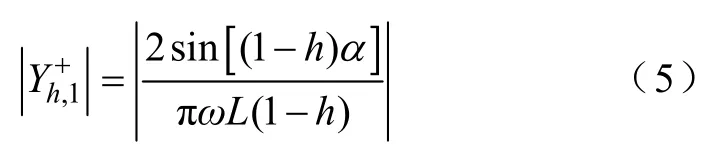
该幅值随谐波次数的增大以1h的速度递减。图 4所示为了元素幅值随触发延迟角和谐波电压次数的变化规律。研究发现，随触发延迟角的增大，并不总是第一行中幅值最大的元素，如当α=70°时，成为幅值最大的元素。但从电力系统实际考虑，单次谐波电压畸变率一般小于5%，因此该转化作用对基波潮流的影响不大。

图4 Y+、Y -第一行元素幅值随触发延迟角和谐波电压次数的变化规律Fig.4 The variation of Y+and Y -first row elements amplitude with harmonic voltage order and firing angles

3.3 TCRs的谐波自导纳

Y+对角线元素表征h次谐波电压与h次谐波电流之间的自耦合效应，即TCRs的谐波自导纳，计算公式如下：

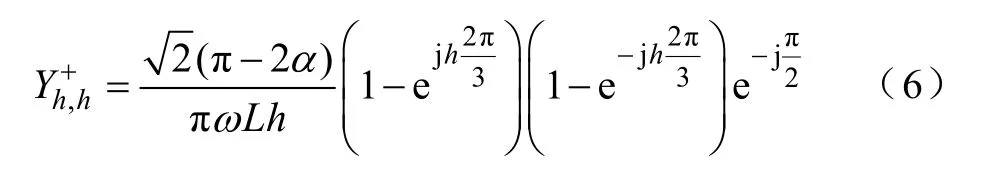
推导发现，对角线元素的幅值以1/h的速度递减，与值为的电抗具有相同的特性，表明TCRs 在谐波频率下等值为的感 性电抗。但该值与TCRs 在基频下的电抗并不相同。由式（2）可知，基频下TCRs的电抗值L1为

式（6）和式（7）可作为TCRs 诺顿等效电路模型中自导纳的修正公式[10]。

3.4 谐波电压与谐波电流的互耦合

TCRs 谐波电压与谐波电流之间的互耦合效应，即某次谐波电压对另外一次谐波电流的影响，可由分析Y+的非对角线元素得出。Y+的非对角元素幅值为

元素的幅值随谐波次数h的增大而递减，同时 元素还随递减。是h次谐波电压与k次谐波电流之间的距离，距离越近，越大。为衡量互耦合作用的强弱，定义参数K+为

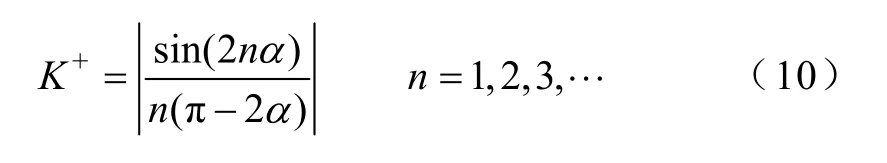
K+随两耦合谐波次数的距离而变化，同时也随触发延迟角α变化，其变化规律如图5 所示。

分析式（9）和图5 可得出以下结论：

（1）对于h次谐波电流，（h-k）次谐波电压对其产生的影响与（h+k）次谐波电压产生的影响具有相同的幅度。

（2）对任意触发延迟角α和组合，K+总小于1，即在Y+矩阵的任一行（h＞1），对角线元素总是幅值最大的元素。

图5 Y+矩阵非对角线元素与对角线元素的比值随触发延迟角的变化规律Fig.5 The ratio variation of Y+non-diagonal elements to the diagonal elements amplitude with the firing angles

（4）当触发延迟角接近90°时，K+接近1，此时对角线元素变得非常小（见式（2）），所以TCRs的谐波耦合作用是很弱的。

3.5 谐波电压共轭的贡献大小研究

为研究TCRs 端口谐波电压共轭对其谐波电流产生的影响，定义K-为Y-元素与Y+对角线元素幅值之比

K-随谐波电压和谐波电流次数之和变化，当k=h=5 时,取得最小值。图6 为K-随触发延迟角的变化规律。可见，K-比K+更小。 触发延迟角α≤60°时，K-小于0.2。这表明，TCRs供电端电压的共轭分量在TCRs 谐波电流产生中的作用要远小于其端电压相量。

图6 Y-矩阵元素与Y+对角元素的比值随触发延迟角的变化规律Fig.6 The ratio variation of Y-elements amplitude to the Y+diagonal elements amplitude with the firing angles

4 TCRs的谐波分析简化模型

通过以上对TCRs 谐波耦合矩阵元素的取值规律和物理意义的分析，得出TCRs的谐波产生有如下特点：

（1）Y+第一列元素表征TCRs 端电压基波分量对TCRs 谐波电流产生的影响。此列元素不含任何谐波电压的作用，是恒流源模型的计算公式。

（2）Y+对角线元素总是每行中幅值最大的（h＞1），且离对角线越近的非对角线元素幅值越大。这表明，对任一次谐波电流，同次谐波电压与其产生的自耦合效应要强于不同次谐波电压与其的互耦合效应，互耦合的程度随谐波电压和谐波电流距离的增大而减小。

（3）TCRs 供电端电压的共轭分量对TCRs 谐波电流产生的作用远小于其端电压相量。

基于谐波耦合矩阵元素的取值规律以及 TCRs的谐波产生特性，可对TCRs的谐波模型进行简化。

（1）Y+模型：忽略谐波电压共轭对各次谐波电流产生的影响

（2）解耦模型：在Y+模型的基础上，进一步忽略Y+的非对角线元素，即忽略谐波电压和谐波电流的互耦合作用，并将基波电压对谐波电流产生的影响表示为恒流源

（3）恒流源模型：在解耦模型的基础上，进一步忽略各次谐波电压和谐波电流之间的自耦合效应，只考虑基波电压的影响，可得出TCRs的恒流源模型，其谐波电流的解析计算公式与式（13）中的相同。恒流源模型由于计算简单方便，是目前各类谐波分析中广泛采用的模型。

5 触发延迟角对简化模型精度的影响

由式（2）可知，任一元素均是触发延迟角α的函数，触发延迟角将影响各简化模型的精度。根据TCRs的运行机理，α在0～90°范围内变化。当系统的供电电压总畸变率为9.68%时，对各模型的精度进行了分析（Matlab Simulink 仿真电路参数见表1）。图7 给出α为10°、40°、80°时，各简化模型与精确模型的仿真波形结果对比。

表1 仿真电路参数Tab.1 Parameters for the simulation models

图7 简化模型结果对比Fig.7 Results comparison of the simplified models

可见触发延迟角较小时，各简化模型和完整模型吻合程度都较高，随触发延迟角的增大，简化模型的精度降低。为精确衡量三种简化模型的准确度，定义E为简化模型和完整模型之间的误差

式中，为由完整模型得出的h次谐波电流值；为由各简化模型得出的h次谐波电流值。

表2 给出了不同触发延迟角时各简化模型与完整模型之间的误差E。当触发延迟角α≤70°时，Y+模型、解耦模型以及恒流源模型的精度都较高；但当触发延迟角α＞70°时，简化模型的结果和完整模型的结果有差异，这是因为随着触发延迟角的增大，谐波电压和谐波电流之间的耦合程度增强。然而，随触发延迟角增大，TCRs 产生的谐波电流实际值也将非常小。因此在工程应用中，若对模型精度要求不高，在较大触发延迟角下仍可采用各简化模型。简化模型的意义在于，可减小谐波潮流计算中形成导纳矩阵的工作量，加快计算速度。特别是当利用TCRs的解耦模型时，各次谐波频率下的谐波潮流可解耦计算，计算量将大为减小。

表2 简化模型与完整模型的误差Tab.2 Discrepancy evaluation for the simplified models

6 结论

本文基于TCRs的谐波耦合矩阵模型，对TCRs的谐波产生特性进行了分析。在TCRs的谐波产生过程中，基波电压的影响最大、与谐波电流次数相同的谐波电压的作用次之、其他谐波电压及其共轭分量与谐波电流的互耦合影响最小。

通过对TCRs的谐波耦合矩阵模型的物理意义和各元素取值规律分析，得出TCRs 诺顿等效电路中谐波自导纳以及经典恒流源模型的解析计算公式。研究了恒流源模型、解耦模型以及Y+模型，在不同触发延迟角时的计算精度。当触发延迟角α≤70°时，各模型精度较高；当触发延迟角α＞70°时，各简化模型都将引入不同程度的误差。结论可为工程中TCRs 谐波模型的合理选择提供理论指导。

[1]刘其辉,蔚芳,康长路.基于电网电压定向矢量变换的SVC 平衡化补偿策略[J].电工技术学报,2009,24(8):147-153.Liu Qihui,Wei Fang,Kang Changlu.Balancing compensation strategy of SVC based on grid-voltage-oriented vector transformation[J].Transactions of China Electrotechnical Society,2009,24(8):147-153.

[2]丁仁杰,刘健,张隽,等.一种基于瞬时无功功率理论的SVC 控制方法[J].电工技术学报,2006,21(5):47-51.Ding Renjie,Liu Jian,Zhang Jun,et al.New control method of SVC based on instantaneous reactive power theory[J].Transactions of China Electrote-chnical Society,2006,21(5):47-51.

[3]刘玉雷,解大,张延迟.静止无功补偿器用于抑制厂用电系统电压波动仿真[J].电力系统自动化,2006,30(16):97-101.Liu Yulei,Xie Da,Zhang Yanchi.Simulation of static var compensator to restrain the voltage fluctuation of electric auxiliary system[J].Automation of Electric Power Systems,2006,30(16):97-101.

[4]张定华,桂卫华,王卫安,等.新型电气化铁道电能质量综合补偿系统的研究及工程应用[J].电工技术学报,2009,24(3):189-194.Zhang Dinghua,Gui Weihua,Wang Weian,et al.Study and application of a new power quality combined compensation system for electrified railway[J].Transactions of China Electrotechnical Society,2009,24(3):189-194.

[5]帅智康,罗安,刘定国,等.静止无功补偿器与有源电力滤波器联合运行系统[J].中国电机工程学报,2009,29(3):56-64.Shuai Zhikang,Luo An,Liu Dingguo,et al.Combined system of static var compensator and active power filter[J].Proceedings of the CSEE,2009,29(3):56-64.

[6]Task Force on Harmonics Modeling and Simulation.Modeling and simulation of the propagation of harmonics in electric power networks,part I:concepts,models and simulation techniques[J].IEEE Transactions on Power Delivery,1996,11(1):452-465.

[7]Task Force on Harmonics Modeling and Simulation.Characteristics and modeling of harmonic sources-power electronic devices[J].IEEE Transactions on Power Delivery,2001,16(4):791-800.

[8]Chang G W,Lin Y.Modeling of nonlinear components for harmonic studies[C].2003 IEEE Power Engineering Society General Meeting,Toronto,Canada,2003:1188-1193.

[9]Montano J C,Gutierrez B J,Lopez O A,et al.Effects of voltage waveform distortion in TCR type compensators[J].IEEE Transactions on Industrial Electronics,1993,40(3):373-383.

[10]Xu W,Marti J R,Dommel H W.Harmonic analysis of systems with static compensators[J].IEEE Transactions on Power Delivery,1991,11(2):183-190.

[11]Rico J J,Acha E.The use of switching function and Walsh series to calculate waveform distortion in thyristor-controlled compensated power circuits[J].IEEE Transactions on Power Delivery,1998,13(4):1370-1377.

[12]Osauskas C M,Wood A R.A frequency domain model of a thyristor controlled reactors[C].Proceedings of the Harmonics and Quality of Power,Athens,Greece,1998:923-929.

[13]Sun Y,Zhang G,Xu W,et al.A harmonically coupled admittance matrix model for AC/DC converters[J].IEEE Transactions on Power Systems,2007,22(4):1574-1582.

[14]郑伟杰,徐文远.TCR 非线性特性的线性耦合导纳矩阵模型[J].中国电机工程学报,2008,28(1):59-64.Zheng Weijie,Xu Wenyuan.Harmonically coupled linear matrix model for harmonic analysis of TCR[J].Proceedings of the CSEE,2008,28(1):59-64.

[15]Medina A,Garcia N.Fast time domain computation of the periodic steady state of systems with nonlinear and time-varying components[J].International Journal of Electrical Power & Energy Systems,2004,26(8):637-643.