PWM激励下异步电机铁耗等值电阻模型

罗富强 夏长亮, 乔照威 王慧敏 宋战锋

（1.天津大学电气与自动化工程学院 天津 300072 2.天津工业大学电工电能新技术天津市重点实验室 天津 300387）

1 引言

为了满足以运行效率优化和转矩性能优化等为目标的高性能控制算法的需求，异步电机等效电路中铁耗等值电阻的准确建模是一个需要重点考虑的方面[1-3]。传统的异步电机等效电路中，电机铁耗表示为一个恒定阻值的电阻，它能够准确反映额定工况下的电机铁耗。但在变频运行时，该模型不再能够准确反映电机铁耗变化[4,5]；另一方面，相对于正弦激励，采用PWM 激励将使电机铁耗增大[6,7]，导致该模型的准确度进一步降低。因此，在采用PWM激励的变频驱动系统中，需要对电机铁耗建立更加准确的等值电阻模型。

目前，诸多文献已对该问题做了相关研究。文献[8-10]通过实验获得不同频率下电机铁耗数据，进而利用数据拟合方法建立考虑运行工况时铁耗等值电阻模型。这种方法能够对一定运行范围内铁耗较好地估计，为了保证估计的精度，需要进行充足的铁耗测量。文献[11]将铁耗模型细分为磁滞、经典涡流和异常涡流三个分量，它们随频率、磁通密度的变化规律各不相同。基于该模型，文献[12]将磁滞损耗和涡流损耗分别表示为两个等值电阻，并通过引入复数磁导率推导了这两个电阻的表达式。该模型构建过程中需要知道与铁磁材料相关的时间常数，但这些参数通常难以获得。文献[13,14]通过在电机等效电路中引入梯形网络，计及铁耗的非线性变化。该模型能够动态地计算铁耗各个分量。文献[15,16]通过修正正弦激励下铁耗分离模型，得到PWM 激励下铁耗模型。该方法能够有效提高PWM激励下铁耗计算精度，但无法直接应用于等值电路中铁耗模型的构建。

本文基于铁耗分离模型，利用三个等值电阻分别等效铁耗的三个分量，根据功率平衡原理，推导了正弦激励下铁耗等值模型。通过分析PWM 激励与正弦激励下铁耗等值电阻间的关系，得到PWM激励下铁耗等值电阻模型。为了确定模型中所需参数，提出了相应的实验方案，该方案通过测量电机三个不同运行频率下的铁耗值实现。仿真和实验结果验证了本文提出模型的正确性和有效性。

2 正弦激励下铁耗等值电阻模型

2.1 铁耗计算模型

根据Bertotti 建立的铁耗分离计算模型，铁耗由磁滞、经典涡流和异常涡流三个分量组成[11]

式中Pfe——总铁耗；

Ph——磁滞损耗；

Pc——经典涡流损耗；

Pe——异常涡流损耗。

磁滞分量Ph取决于似稳状态下磁滞环所包围的面积和磁通密度交变的频率，如下式所示

式中Kh——磁滞系数；

Gfe——铁心质量；

f——磁通密度交变频率；

Bm——磁通密度幅值；

x——斯坦梅茨系数。

经典涡流分量Pc、异常涡流分量Pe取决于磁通密度的变化率，分别通过下式计算

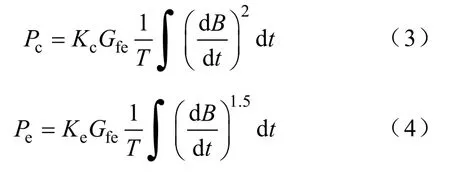
式中Kc，Ke——经典涡流、异常涡流系数；

B——磁通密度变化波形。

当磁通密度波形为正弦变化时，化简式（2）～式（4），则铁耗可表示为

2.2 传统铁耗等值电阻模型

传统的异步电机等效电路如图1 所示，其中电机的铁耗由电阻Rm表示，铁耗计算式为

式中Em——激磁电动势；

Rm——铁耗等值电阻；

S——铁心截面积；

N——每相绕组的匝数。

图1 异步电机的等效电路Fig.1 Equivalent circuit of IM

由式（6）可知，若采用该等值电阻计算铁耗，铁耗计算值近似随磁通密度和频率乘积的二次方变化。由式（5）可知，总铁耗中铁耗各个分量随磁通密度和频率的变化规律各不相同，其中磁滞损耗随磁通密度的x次方、频率的一次方变化，经典涡流损耗随磁通密度、频率的二次方变化，异常涡流损耗随磁通密度、频率的1.5 次方变化。对比式（5）和式（6）可知，采用图1 中等值电阻计算铁耗时，其计算结果随频率、磁通密度的变化规律与经典涡流损耗相同。电机正常运行频率范围内，经典涡流损耗所占总铁耗的比例相对磁滞损耗较小，且随着频率降低，该比例将进一步降低。因此，电机变频运行状况下，采用图1 中铁耗等值电阻计算电机的铁耗将带来较大的计算误差。

2.3 改进的铁耗等值电阻模型

由以上分析可知，为了提高电机变频运行状况下铁耗的计算精度，需要考虑铁耗各个分量随磁通密度和频率变化规律不同的影响，因此有必要为每个铁耗分量分别等效一个电阻，则相应的异步电机等效电路如图2 所示。

图2 考虑铁耗各个分量的异步电机等效电路Fig.2 Equivalent circuit of IM considering each component of the total iron loss

图2 中，Rh、Rc和Re分别为表示磁滞损耗、经典涡流损耗和异常涡流损耗的等值电阻。根据等效电路，各损耗分量的计算如下

式中Im——励磁电流；

Xm——励磁电抗；

Lm——励磁电感。

为了根据式（7）推导Rh、Rc和Re三个电阻的表达式，需要知道铁耗的各个分量，本文基于铁耗分离模型，推导这些量在等值电路中的表达方式。铁耗分离模型描述了铁磁材料中铁耗随磁通密度及频率的变化关系，根据此模型计算铁磁材料的铁耗，需要知道磁通密度在铁磁材料中的分布情况。由于电机定子铁心内磁通密度非均匀分布，为了准确计算铁耗，需要将电机铁心分块。一般地，若将电机铁心分割为足够小的n块，则可认为每块的磁通密度分布均匀，假设磁通密度的最大值为Bm、第i块的磁通密度为Bi，且存在关系Bi=KiBm，则根据式（5），电机铁耗各个分量为

若忽略铁磁材料饱和，则磁通密度幅值Bm与励磁电流Im之间为线性关系，即

令式（7）和式（8）中铁耗各个分量相等，并联立式（9），则各个铁耗等值电阻可表示为

由式（10）可知，改进后的模型中铁耗各分量的等值电阻随频率及励磁电流变化而变化，且变化规律各不相同。其中磁滞损耗电阻随频率的一次方、励磁电流的2-x次方变化；经典涡流损耗电阻为恒值，不随频率、励磁电流发生变化；异常涡流损耗电阻随频率和励磁电流乘积的1.5 次方变化。各电阻分量的变化规律与铁耗分离模型相同，因此采用式（10）计算电机的铁耗，将能更加真实地反映铁耗的实际变化情况。

3 PWM 激励下铁耗等值电阻模型修正

在非正弦激励下，相对于正弦激励，异步电机铁耗随输入电压波形的不同而发生变化，且其变化规律与输入电压波形存在紧密联系。若忽略绕组损耗，则输入电压与磁通密度变化率的关系为

式中V——输入电压；

N——线圈匝数；

S——铁心截面积。

若输入电压为PWM 波形，如图3 所示，其幅值为Vm1，基波频率为f，每半周期的脉冲数为p，第i个脉冲的宽度为τi，起始时间为ti。由式（11）可知，铁心内磁通密度变化率为

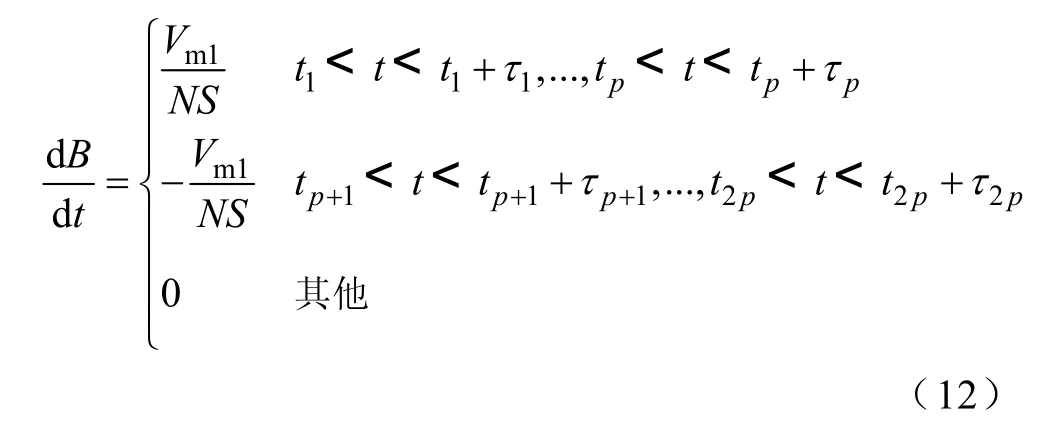
图3 PWM 电压波形Fig.3 Voltage waveform of PWM

将式（12）代入式（3），则PWM 激励下经典涡流损耗为

根据式（5），该PWM 波形中基波分量产生的经典涡流损耗为

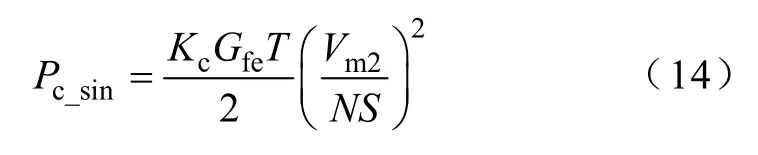
式中Vm2——PWM 波形基波电压幅值，且Vm2=mVm1，其中m为PWM 波形的调制 系数；

T——基波周期。

由PWM 波形的性质可知，其半周期脉冲宽度 之和、调制系数和基波周期存在关系：，则由式（13）和式（14）可得PWM 激励下和其对应基波正弦电压激励下经典涡流损耗的关系为

同理可得，两种激励下异常涡流损耗的关系为

由于两种激励下磁通密度幅值相等，则由式（2）可知，二者的磁滞损耗相等，即

式（15）～式（17）描述了PWM 激励与正弦激励下电机铁耗间关系，由表达式可知，调制系数是影响PWM 激励下铁耗变化的主要因素。由于调制系数总是小于1，故相对于正弦激励，PWM 激励下铁耗将增大，且增大部分由涡流损耗的增加造成。调制系数越低，铁耗增大越多。

根据式（15）～式（17），在已知正弦激励下铁耗各个分量时，可得到PWM 激励下铁耗值。据此对式（10）中铁耗等值电阻进行修正，则其表达式为

4 模型参数确定

为了使用以上模型计算电机的铁耗，需确定模型中参数。由于铁耗分离模型系数及几何参数通常难以预先获取，给模型参数的直接计算造成困难，为此，本文提出一个确定模型所需参数的实验方案，步骤如下：

（1）分离额定状况下总铁耗为磁滞损耗、经典涡流损耗和异常涡流损耗分量。

铁耗各个分量随磁通密度和频率的变化规律各不相同，因此通过测量不同磁通密度、频率下铁耗值，可将总铁耗分离为各个分量。由于电机正常运行条件下磁通密度近似保持不变，因此分离过程中可只考虑频率对铁耗的影响。空载条件下，分别测量频率为f1、f2和f3，同时保持定子电流为额定励磁电流情况下的铁耗，分别为Pfe1、Pfe2和Pfe3。由于定子电流相同，则磁通密度幅值相同，因此根据式（8）可得

根据式（19），运用最小二乘法，可解得a、b和c，则额定频率fN下铁耗的各个分量为

（2）计算额定状况下各个铁耗等值电阻分量。

在计算出铁耗各个分量后，根据图2，空载条件下，可得额定频率下各个铁耗等值电阻为

式中Us0——空载输入电压；

Is0——空载定子电流；

Zs——定子阻抗。

（3）计算任意频率、励磁电流条件下各个铁耗等值电阻分量。

对式（10）重新整理，可得

联立式（21）、式（22）和式（18）可得任意运行条件下铁耗等值电阻为

式（23）描述了各个铁耗等值电阻分量在任意频率、调制系数下的变化规律。

特别地，若频率、调制系数二者的变化存在联系，如调制系数随频率成正比变化，则式（23）可写为

由于电机正常运行状况下Im变化较小且异常涡流损耗分量占总损耗的比例较小，因此若忽略Im的影响，则铁耗等值电阻的各个分量将均随频率成正比变化，因此三者可合并为一个电阻，如下式所示

此时，确定模型参数无需进行铁耗分离，铁耗等值电阻可采用传统的铁耗测量方法确定，即通过空载实验计算铁耗等值电阻。与传统铁耗等值电阻不同，该模型中铁耗等值电阻随频率成正比变化，同时计及调制系数的影响，而传统铁耗等值电阻则保持不变。

5 仿真与实验验证

5.1 仿真验证

为验证改进的铁耗等值电阻模型的有效性，分别利用传统模型和改进模型，对一台11kW 异步电机的铁耗进行仿真计算，并将计算结果与Ansoft 有限元分析的结果进行对比。异步电机参数见下表。

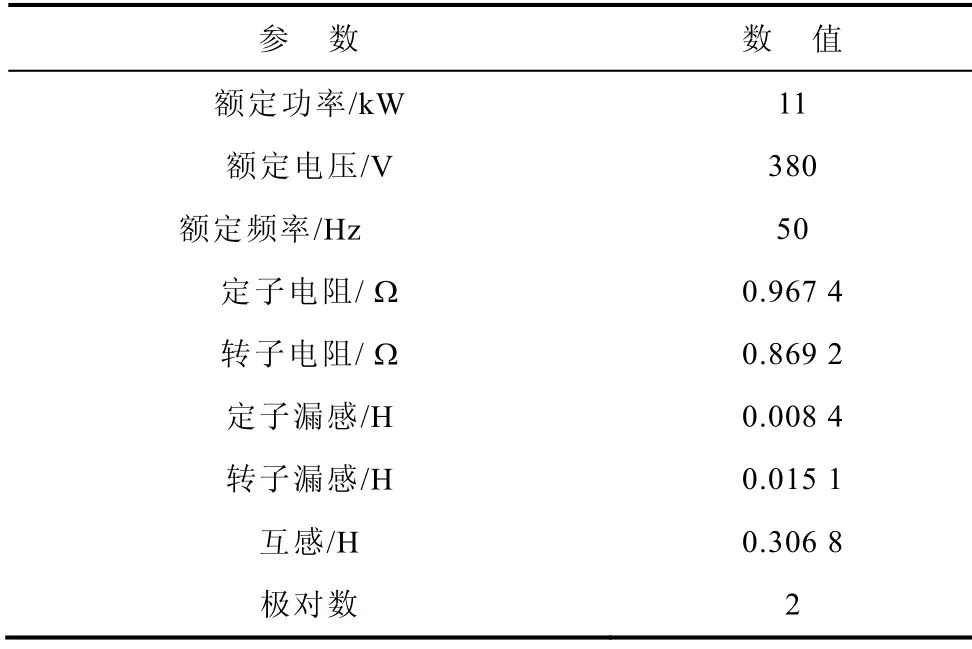
表 异步电机参数Tab. Parameters of IM

利用有限元法在三个不同频率下的铁耗计算结果，根据第4 节中模型参数确定方法，空载条件下，频率为50Hz 时，改进模型中各个铁耗等值电阻计算值Rh0为1 801Ω，Rc0为8 101Ω，Re0为∞Ω，此时传统等值电阻为1 473Ω。

将图2 所示等效电路中三个铁耗等值电阻表示为一个总铁耗等值电阻，当电机由PWM 激励，励磁电流保持不变时，该等值电阻与频率、调制系数的关系如图4 所示。

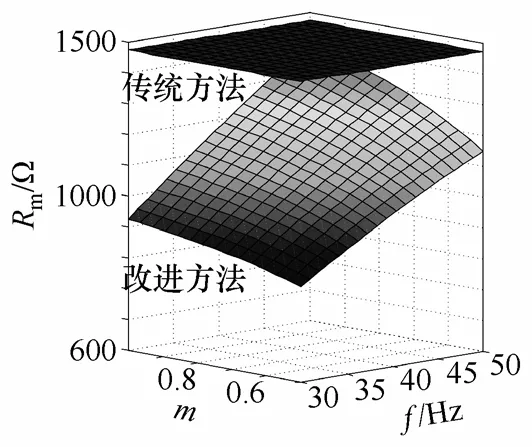
图4 总铁耗等值电阻Fig.4 Total equivalent resistance of iron loss

由图4 可知，改进后的总铁耗等值电阻随频率和调制系数变化而变化，频率、调制系数越小，总铁耗等值电阻越小。而传统铁耗等值电阻则一直保持不变。由图4 还可看出，随着频率的减小，调制系数对铁耗等值电阻的影响变小，因为调制系数只影响涡流损耗的变化，而频率降低时涡流损耗占总铁耗的比例降低。

图5 为正弦激励下，采用改进方法和传统方法的铁耗计算结果。

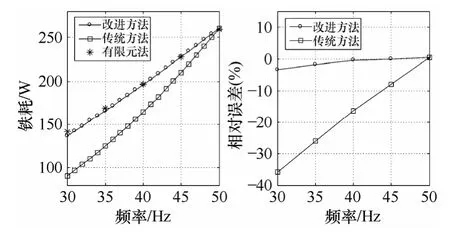
图5 正弦激励下两种方法的铁耗计算结果Fig.5 Comparison of iron loss calcultion results under sinusoidal excitation

由图5 可知，传统方法能以较高精度计算电机额定频率运行时的铁耗，但电机运行于较低频率时，其铁耗计算将出现较大偏差，且频率越低，偏差程度越大。当频率为30Hz 时，其计算结果相对于有限元法的误差为35.2%。改进方法则能以较高精度计算各运行频率下电机铁耗，频率为30Hz 时，其计算结果相对于有限元法的误差为3.6%，比传统方法提高了31.6%。正弦激励下，改进方法有效提高了铁耗计算的准确度。

图6 为正弦激励和PWM 激励下，有限元法的铁耗计算结果。

图6 正弦激励和PWM 激励下有限元法铁耗计算结果Fig.6 Iron loss caculation results under sinusoidal and PWM excitation

由图6 可看出，与正弦激励相比，PWM 激励下，电机的铁耗增加。同时，随调制系数降低，电机的铁耗增大，频率为50Hz、调制系数为0.6 时，相对于正弦激励，铁耗增大26.9%。

图7 为PWM 激励下，采用改进方法和传统方法在不同调制系数下的铁耗计算结果。

图7 PWM 激励下两种方法的铁耗计算结果Fig.7 Comparison of iron loss under PWM excitation

由图7 可以看出，改进方法在不同频率、不同调制系数下，均能以较高精度计算电机铁耗，其相对误差保持在7%以内，传统方法则存在较大误差。另外，相对于正弦激励，由于传统方法未计及调制系数的影响，其计算误差进一步增大，在额定频率下，将产生10.0%～21.2%的相对误差，这部分误差是由PWM 激励下铁耗的增加造成。由图7 还可以看出，传统方法的计算误差随调制系数的减小而增大，调制系数为0.6、频率为30Hz 时，其计算误差为47.2%，而此时改进方法的计算误差为6.8%，相对于传统方法降低了40.4%。

5.2 实验验证

对一台采用恒压频比控制的异步电机的铁耗进行了实验测量。电机额定功率为1.1kW，额定电压为380V，额定频率50Hz，额定功率因数为0.6。为了测量PWM 激励下铁耗的增加以及提高测量准确度，实验中使用示波器观测电机定子输入电压、电流及瞬时功率波形。电机空载条件下，电压为380V、频率为50Hz 时，定子电流、输入电压和瞬时功率的实验测量波形如图8 所示，此时电机的铁耗测量结果为114W。

图8 实验测量波形Fig.8 Measured waveforms by experiment

恒压频比控制下，由于调制系数随电压成正比变化，其也将随频率成正比变化。因此，根据式（25），此时的铁耗等值电阻为3767 Ω，则此控制方式下，两种方法的铁耗计算结果及其与实验测量值的对比如图9 所示。

图9 恒压频比控制下两种方法的铁耗计算结果Fig.9 Comparison of iron loss under constant V/F control

由图9 可知，两种方法均能在额定频率下以较高精度计算铁耗。随着频率降低，两种方法的计算精度均有所降低，但对比图中变化曲线可以看出，二者的计算精度不同。由于改进模型中，铁耗等值电阻随频率按照式（25）变化，而传统模型中铁耗等值电阻保持不变，因此，改进方法相对于传统方法有较高的计算精度，在频率为30Hz 时，相对于传统方法，提高了29.8%。造成改进方法在频率降低时计算误差增大的原因可能为：频率降低时铁耗的测量值相对偏高。实验中铁耗的测量值为实际铁耗与杂散损耗之和，在实验测量条件下，电机的负载保持不变，故杂散损耗不随频率发生变化[17]，而铁耗随频率减小而减小。因此频率降低时，铁耗实际值占铁耗测量值的比例将减小，从而使铁耗的测量值偏高。

6 结论

本文建立了PWM 激励下异步电机的铁耗等值电阻模型，模型中采用三个变化的电阻等效电机的铁耗，从而计及铁耗的非线性变化。其中，运行频率降低和调制系数减小均将导致铁耗等值电阻减小。仿真和实验结果表明，改进模型有效提高了铁耗的计算精度，较为真实地反映了电机铁耗的变化规律，为建立更加准确的电机仿真模型打下了较好的基础。

[1]Bijan Zahedi,Sadegh Vaez Zadeh.Efficiency optimization control of single-phase induction motor drives[J].IEEE Transactions on Power Electronics,2009,24(4):1062-1071.

[2]Nasir M Uddin,Sang Woo Nam.New online loss-minimization-based control of an induction motor drive[J].IEEE Transactions on Power Electronics,2008,23(2):926-933.

[3]崔纳新,张承慧,吕志强,等.基于电压空间矢量的电动汽车电驱动系统高效快转矩响应控制[J].电工技术学报,2009,24(3):61-66.Cui Naxin,Zhang Chenghui,Lü Zhiqiang,et al.Fast torque response control of high efficiency drives in electric vehicles based on voltage space vector[J].Transactions of China Electrotechnical Society,2009,24(3):61-66.

[4]Kirschen D S,Novotny D W,Suwanwisoot W.Minimizing induction motor losses by excitation control in variable frequency drives[J].IEEE Transactions on Industry Applications,1984,IA-20(5):1244-1250.

[5]Jian T,Schmitz N,Novotny D.Characteristic induction motor slip values for variable voltage part load performances optimization[J].IEEE Transactions on Power Apparatus and Systems,1983,PAS-102(1):38-46.

[6]Boglietti A,Ferraris P,Lazzari M,et al.Influence of modulation techniques on iron losses with single phase DC/AC converters[J].IEEE Transactions on Magnetics,1996,32(5):4884-4886.

[7]Boglietti A,Cavagnino A,Lazzari M,et al.Predicting iron losses in soft magnetic materials with arbitrary voltage supply:an engineering approach[J].IEEE Transactions on Magnetics,2003,39(2):981-989.

[8]王建渊,安少亮,李洁,等.考虑主磁路饱和与铁损的异步电机模型[J].电工技术学报,2010,25(10):44-50.Wang Jianyuan,An Shaoliang,Li Jie,et al.Modeling of induction motor considering main flux saturation and iron loss[J].Transactions of China Electrotechnical Society,2010,25(10):44-50.

[9]Moulahoum S,Touhami O.An approach to an induction machine modeling in presence of saturation and iron loss[C].IEEE Power Engineering Society General Meeting,2005:2272-2276.

[10]Emil Levi,et al.Iron loss in rotor-flux-oriented induction machines:identification,assessment of detuning,and compensation[J].IEEE Transactions on Power Electronics,1996,11(5):698-709.

[11]Bertotti G.General properties of power losses in soft ferromagnetic materials[J].IEEE Transactions on magnetic,1988,24(1):621-630.

[12]Buecherl D,Herzog H.Iron loss modeling by complex inductances for steady state simulation of electrical machines[C].International Symposium on Power Electronics Electrical Drives Automation and Motion(SPEEDAM),2010:878-883.

[13]Hui S Y R,Zhu J.Numerical modelling and simulation of hysteresis effects in magnetic cores using transmission-line modelling and the Preisach theory[J].IEE Proceedings Electric Power Applications,1995,142(1):57-62.

[14]Hui S Y R,Zhu J G,Ramsden V S.A generalized dynamic circuit model of magnetic cores for low-and high-frequency applications II.circuit model formulation and implementation[J].IEEE Transactions on Power Electronics,1996,11(2):251-259.

[15]Amar M,Kaczmarek R.A general formula for prediction of iron losses under nonsinusoidal voltage waveform[J].IEEE Transactions on Magnetics,1995,31(5):2504-2509.

[16]Gmyrek Z,Boglietti A,Cavagnino A.Estimation of iron losses in induction motors:calculation method,results and analysis[J].IEEE Transactions on Industrial Electronics,2010,57(1):161-171.

[17]Boglietti A,Cavagnino A,Ferraris L,et al.Induction motor equivalent circuit including the stray load losses in the machine power balance[J].IEEE Transactions on Energy Conversion,2008,23(3):796-803.