汉字编码原理及冗余度分析

赵洪鳞 林贵州 陈水钦 蔡侨燕

(东莞理工学院 计算机学院，广东东莞 523808)

随着信息革命的发生，人们的生活发生了翻天覆地的变化，最近几十年，信息在人们的生活中越来越重要，覆盖面也越来越广，而且越来越多的实物转化为信息进行跟踪存储，未来的世界必定是信息的时代。特别是信息化的概念提出之后，越来越多的国家和地区积极投入信息化的研究开发，已经有很多具有跨时代意义的产品产生。而中国要与世界接轨，汉字被世界接受是必不可少的，因此汉字编码对中国来说具有跨时代意义。

1 汉字处理流程

汉字处理流程粗略来讲是指通过外界输入交换操作，经过内部智能处理，把输入要求输出的信息进行输出。详细来讲是通过汉字输入码，把想要的信息输入智能系统，汉字输入码通过汉字交换码表，找出与输入码相对应的汉字机内码，然后再根据汉字机内码，找出与机内码对应的汉字点阵码，把对应的点字码在屏幕进行输出或者在打印机上打印输出或通过汉字字形控制码调整打印各种风格的字体或字形。其流程图如图1所示 (根据文献 ［1］改进):

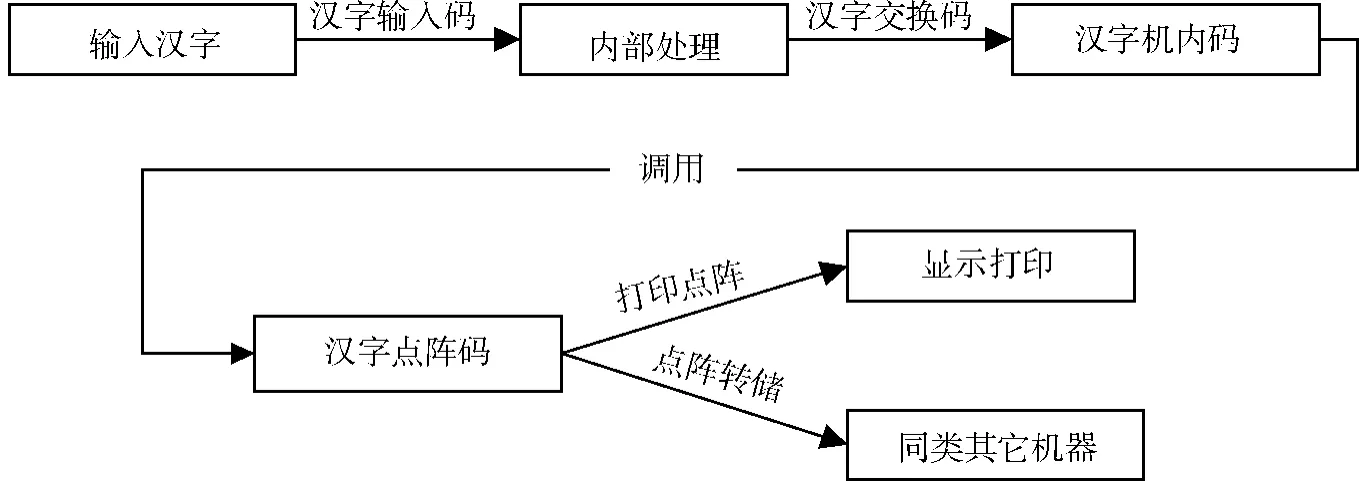
图1 汉字处理流程图

2 汉字编码类型

在计算机标准键盘上，汉字的输入和西文字符的输入有很大的不同。西文输入，击一次键就能直接输入相应的字符或代码，键入就是输入。但是在计算机进行汉字输入时，键入是指在键盘上的操作，输入是指把所需的汉字或符号送到指定位置，是键入的目的。不同的输入法对应不同的汉字输入码编码，不同的汉字输入码操作不同，但是可以得到相同结果。其中汉字编码主要分为汉字字音编码、汉字字形编码、汉字数字编码、音形混合码等。

在世界范围内，不同编码类型在编码规则上有很大不同，目前国际上的通用码是ASCII(美国信息交换标准编码，美标)。而在汉字编码中，具有代表性的主要是GB2312、BIG5码与GBK。GB2312是简体中文字符集的中国国家标准，全称为“信息交换用汉字编码字符集—基本集”，几乎所有的中文系统和国际化的软件都支持GB2312，是国标码 (中华人民共和国国家标准交换用汉字编码);BIG5码是针对繁体汉字的编码，在香港和台湾的电脑系统中应用的比较普遍;GBK全名为汉字内码扩展规范，是对GB码的扩展字符编码，对多达2万多字的简繁汉字进行了编码。GBK与GB2312编码兼容，向下支持ISO10646.1国际标准，是前者向后者过度的启程标准。

3 汉字编码

汉字的编码不是唯一的，主要有机内码与字型码。汉字机内码是指计算机内部存储、处理加工和传输汉字时所用的由0和1符号组成的代码。输入码被接受后就由汉字操作系统的“输入码转换模块”转换为机内码，与所采用的键盘输入法无关。机内码是汉字最基本的编码，不管是什么汉字系统和汉字输入方法，输入的汉字外码到机器内部都要转换成机内码，才能被存储和进行各种处理。

机内码与区位码稍有区别。汉字区码和位码都在1－94之间，若直接用区位码做机内码会与ASCII码混淆。为了避免冲突，需要避开基本ASCII码中的控制码 (00H－1FH)，还要与ASCII中的字符相区别。为了相区别这两点，我们将汉字编码加上2020H得到国标码，再由国标码加上8080H得到机内码。如图2所示:

图2 汉字编码图

汉字字型码又称字模，用于汉字在显示屏或打印机输出。汉字字型码通常有点阵和矢量表示这两种表示方式。用点阵表示字型时，汉字字型码指的是这个汉字字型点阵的代码。根据输出汉字的要求不同，点阵的多少也不同。简易型汉字为16×16点阵，提高型汉字为24×24点阵，32×32点阵，48×48点阵等等。点阵规模愈大，字型愈清晰美观，所占存储空间也愈大。而矢量表示方式存储的是描述汉字字型的轮廓特征，当要输出汉字时，通过计算机的计算，由汉字字型描述生成所需大小和形状的汉字点阵。矢量化字型描述与最终文字显示的大小，分辨率无关，因此可以产生高质量的汉字输出。Windows中使用的TrueType技术就是汉字的矢量表示方式。

汉字的显示和输出，普遍采用点阵方法。不同字形的汉字，就有不同的点阵字形。每个汉字的点阵都是由二进制0和1组成的矩形方阵，0代表没有，1代表有点，将0和1分别用不同颜色画出，就形成一个汉字字形，构成它在字库中的字模信息。

16×16点阵的汉字其点阵有16行，每一行有16个点，这样一个16×16点阵的汉字需要用2×16，即32个字节来存放。所以显示一个汉字时，需要一次性读取32个字节，并将每两个字节为一行打印出来，即可形成一个汉字。同理，24×24点阵和32×32点阵的汉字规则分别要用72个字节和128个字节存放一个汉字。

以“汉”字为例，对其进行16X16点阵的编码和显示原理，如图3所示:

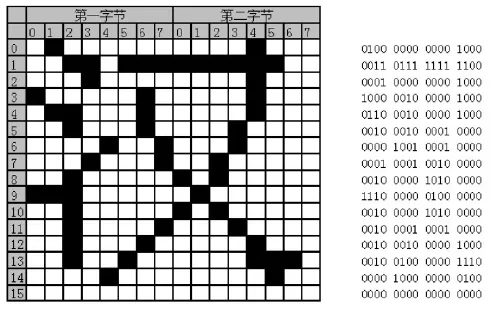
图3 16X16点阵的编码和显示原理

4 编码分析

根据编码原则，在保证编码覆盖范围尽可能广的同时，也要考虑编码存储容量和编码传输速度。下面我们从信息论的角度分析编码原则。

4.1 无错编码码率

设X为一信源字母集，U={0，1，…，D－1}为D进码字字母集，n，k为正整数，映射f:Xn→UK称为等长编码，映射φ:UK→Xn称为相应的译码，对每个xn∈Xn，f(xn)=uk∈UK称为码字，码字全体构成的集合称为由f编出的码。R=k/n称为f的编码速率，简称为码率。R的单位是D进码字字母/信源字母，即平均每个信源符号用R个D进数字表示如用二进制单位，则R=k/n*log2D比特/信源字母。

因为映射f:Xn→UK必须是一一映射， X=N(X表示集合X元素个数)，所以 Uk≥Nn。所以R=k/n*log2D≥log2N。

采用等长编码容易识别编码，但是如果信源中需要编码的字符量过大，会占用过多的存储空间。采用变长编码可以节省存储空间，但是根据编码区分信源字母上会增加难度。

例:以1，2，3，4为信源字母集，对其用等长和变长编码，如图4所示。

解:X =4，用二进制编码，码率R=k/n*log2D≥log24=2。

图4 二进制等长和变长编码

等长编码把译码从前往后一两个为一组，很容易编译出信源字母顺序。例01001011，译码为2134。

变长编码针对相同的译码采用不同的顺序可能会有不同的结果。例0111，可以译为123，也可以译为04。

针对汉字编码，普遍采用的等长编码，如果能够提出简易的译码函数，或者保证每一个码字都不是其他码的前缀，就可以采用变长编码，提高汉字编码质量。

4.2 唯一可译码

不同的汉字在使用中有不同的概率，汉字的数量又太庞大，很多字在现代生活已经不使用。如果我们对出现概率比较大的字，尽可能采用短的代码组表示，使用概率比较小的字采用长编码，即可提高编码效率。牵涉到编码字母概率的问题，也就是信源熵的问题。

信息具有不确定性，我们用熵来度量这种不确定性，熵也可以说是每个信号的平均信息量。香浓提出的熵的公式为:

其中p(x)为信号x在X中出现的概率。熵也成为香浓熵，信源熵。从中可以看出，等概率分布时熵值最大，反应的实质是其包含了最少的信息量，其不确定量最大。

根据克莱夫特不等式，码字字母取值与D进制字母集的即时码 (称唯一可译编码f为即时编码，如果f编出的码字集中，没有一个码是其他码的前缀，f编出的码称为即时码)，其码字长分别为l1，l2，…，lm时必须满足。我们可以证明码长l(x)=［log(1/p(x))］+1(取整)满足克莱夫特不等式，因此可以构造唯一可译码。该可译码平均码长:

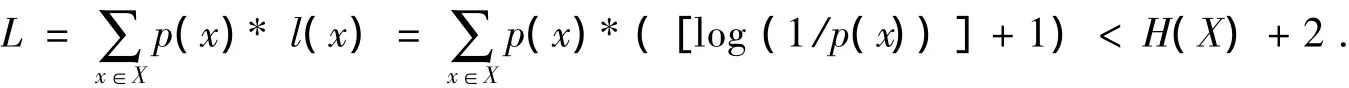
它比理论编码最优值——信源熵H(X)只多2个比特。

4.3 冗余度

根据文献 ［2］，用H(X，Y)表示联合熵，它是随机变量 (X，Y)的联合分布为p(x，y)=p(X=x，Y=y)的熵:

用H(Y|X)表示随机变量X条件下Y的熵，用p(y|x)=p(Y=y|X=x)表示条件概率分布:

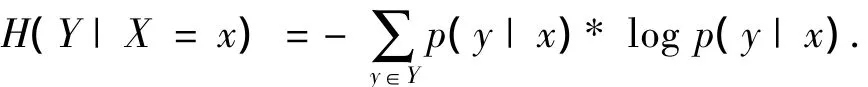
称H∞(X)为平稳信源X的熵率，熵率的两种等价形式:

1)H∞(X)=(1/n)*H(X1，X2，…，Xn);

2)H∞(X)=H(Xn|X1，X2，…，Xn－1);

冗余度表征了信源信息率的多于程度，是描述信源客观统计特征的一个物理量。冗余度越大，则信息的效率就越低;反之效率越高。

由广义Shannon不等式，有

对于记忆信源，最小单个消息熵应为H∞(X)，即从理论上看，对于有记忆信源只需传送H∞(X)即可，但是前提是必须要掌握全部概率统计特征。但是人们智能掌握有限的n阶，这是至少需要传送信息熵:

那么与理论值相比，就多传送了Hn(X)－H∞(X)。因此可以用信源效率η，定量描述信源的有效性:

如在英文中，26个字母和空格的使用频率如表1所示 (根据文 ［3］，以统计8 000字为例):

独立等概率 (即每个字符相互独立且出现的概率是1/27)的情况下，

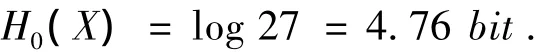
独立不等概率的情况下，

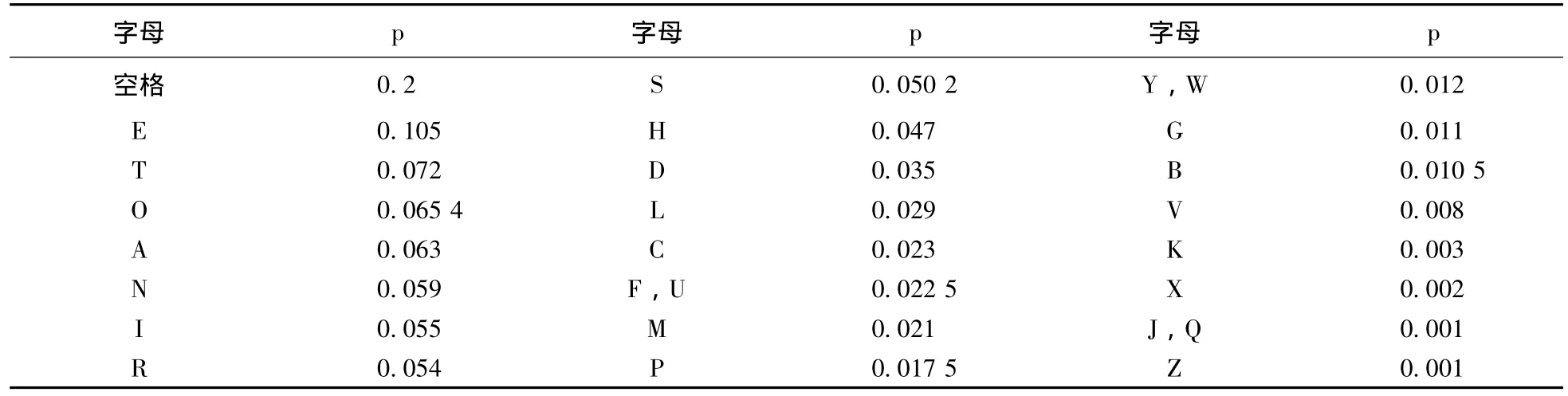
表1 字母和空格的使用频率

如果有完整统计，可以统计出字母的相关性，得出条件概率，计算出条件熵，直至H∞(X)。

由于采用的逼近方法和所取的样本不同，推算值也可能不同。根据Shannon的推断值，我们取H∞(X)为:

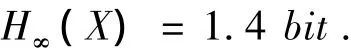
则可以计算出:

信源效率: η=H∞(X)/Hn(X)=0.29;

相对冗余度: r=1－H∞(X)/Hn(X)=0.71。

这就说明，英文信源从理论上看有效成分只有71%，可以根据这一容量对其进行压缩编码。

对于其他文字，也有不少人做了大量的统计工作，如表2［3］:

表2 各种文字的信源对比

从表中可以看出，中文的各层次上都比其他语言高出很多，这也说明中文是最复杂的语言，也是最难学的语言。中文对信息传达的效率不高，冗余度大，由此可以看出汉字还可以对其进行改进，进行完善。特别是对其进行信息化编码，更有利于简明高效的传达信息。

从码率和熵的角度可知存在最优编码。随着人们生活的改变，汉字熵也会改变。从汉字的冗余度进行分析可知，汉字传输信息效率还可以改进提高。从目前的形势看我们还没办法做到最优编码，但是随着理论的深化和技术的完善，一定可以找到更有效的编码方案。

［1］卢永奇.信息编码与汉字处理原理［J］.云南大学师范报:自然科学版，2004，24(2):24－27.

［2］叶中行.信息论基础［M］.北京:高等教育出版社，2003.

［3］熊辉.数学建模［M］.北京:中国人民大学出版社，2011:193－195.