利用F-展开法求解ZK-BBM方程
鱼翔
(西北大学数学系,陕西 西安 710069)
利用F-展开法求解ZK-BBM方程
鱼翔
(西北大学数学系,陕西 西安 710069)
利用F-展开法求解出了ZK-BBM方程的双周期波解,并在极限形式下得到了ZK-BBM方程的孤波解和单周期波解.从而丰富了该方程解的理论.此方法也可适用求解其它非线性发展方程.
F-展开法;ZK-BBM方程;孤波解;周期波解
1 引言
文献[1]提出并利用扩展的双曲正切法研究一类重要的组合方程ZK-BBM方程.形式如下:
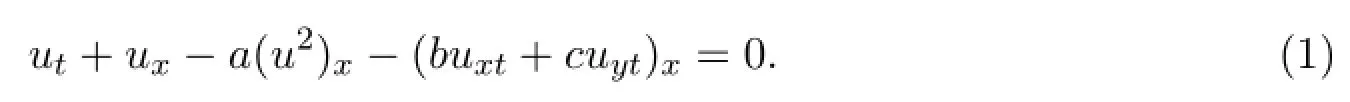
文献[2]则运用同伦摄动法求出了该方程的近似孤波解.而在研究非线性微分方程周期波解的求解方面F-展开法[35]和Jacobi椭圆函数法[6]则是很有效的工具.本文利用F-展开法求出了方程(1)的用Jacobi椭圆函数表示的双周期波解,并在极限情形下得到该方程的孤波解和单周期波解.
2 ZK-BBM方程行波解的一般形式


3 ZK-BBM方程的周期波解
对于P,Q,R与方程(3)的解F(ξ)之间的关系如表1所示:

表1 P,Q,R与方程(3)的解F(ξ)之间的关系

4 ZK-BBM方程的孤立波解及单周期波解

5 结论
从本文求解过程可看出,利用F-展开法求出了ZK-BBM方程的双周期波解,孤波解,单周期波解,且所得到的结果较丰富,同时还可以用该方法对更多的非线性数学物理方程进行求解.
[1] Wazwaz A M. The extend tanh method for new compact and noncompact solutions for the KP-BBM and ZK-BBM equations[J]. Chaos, Solitons and Fractals, 2008,38:1505-1516.
[2] 陈亮,尚亚东.同论摄动法与ZK-BBM方程的近似孤波解[J].广东大学学报:自然科学版,2010,9(3):16-19.
[3] Wang M L, Li X Z. Application of F-expansion to periodic wave solution for a new hamiltonian amplitude equation[J]. Chaos, Solitons and Fractals, 2005,24:1257-1268.
[4] 田景之,杨千山.用F-展开法解Variant Boussinesq方程组[J].西南民族大学学报:自然科学版, 2007,33(5):1058-1060.
[5] 李保安,尤国伟,秦青.BBM方程的周期波解和孤立波解[J].河南科技大学学报:自然科学版,2004,25(5):70-73.
[6]刘式适,付遵涛,刘式达,等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报, 2001,50(11):2068-2073.
Using F-expansion method for solving ZK-BBM equations
Yu Xiang
(Department of Mathem atics,Northwest University,Xi′an 710127,China)
By F-expansion method, doubly periodic wave solutions of ZK-BBM equation was solved. In the limit cases, the solitary wave solutions and single periodic wave solutions of the ZK-BBM equation are obtained. All these enrich the theory of solutions of this equation. This method also can be applied to solve other nonlinear evolution equation.
F-expansion method, ZK-BBM equation, solitary solution, periodic solutions
O 175.2
A
1008-5513(2012)02-0228-04
2011-03-12.
国家自然科学基金(10671156).
鱼翔(1985-),硕士生,研究方向:偏微分方程.
2010 MSC:35Q 58

