高次非线性薛定谔微分方程的新精确解

董长紫

（陇东学院 数学系，甘肃 庆阳 745000）

非线性薛定谔方程是数学物理中一类重要的非线性演化方程。在量子力学、非线性光学、电磁学、等离子体理论、固体物理及玻色-爱因斯坦凝聚等众多领域中有着广泛的应用。关于非线性微分方程的求解，已出现了许多精巧的方法。如齐次平衡法[1,2]、双曲函数展开法[3,4]、Jacobi椭圆函数展开法[5,6]、Riccati方程映射法[7]、行波解法[8]等等。2005年，赵敦[9]给出了解非线性偏微分方程精确解的一种有效的方法——直接截断法。本文将以直接截断法为基础，结合Jacobi椭圆函数，构造方程(1)含椭圆函数的精确解。

对于给出的偏微分方程：假设方程(2)有如下形式的解：

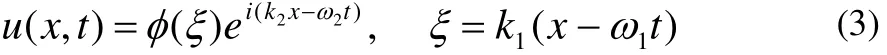
其中 k1,k2,ϖ1,ϖ2均是要被确定的参数。现在，只需要处理普通的微分方程：

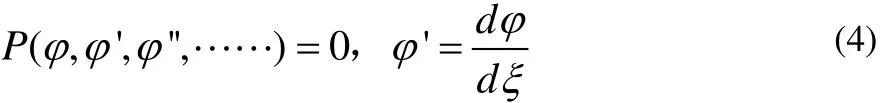
第一步：假设φ()ξ有以下的形式：

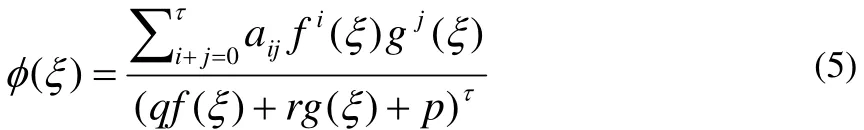
其中aij， p ， q， r 均是待确定的参数，指数τ的值则可以通过平衡方程(4)中的最高次非线性项和最高次的偏微分项的次数而确定。 f(ξ)， g(ξ)满足以下椭圆函数的条件：

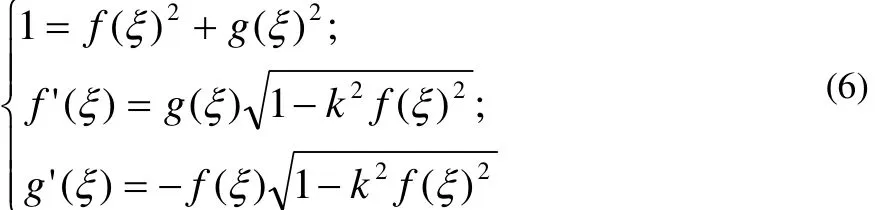
Jacobi椭圆函数具有一些非常重要的性质：

（1）三角函数的性质

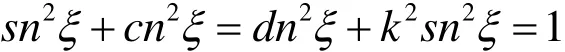
（2）Jacobi椭圆函数的微分

（3）当k→0时，Jacobi椭圆函数退化为三角函数

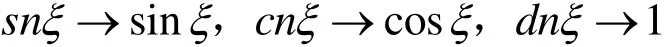
（4）当k→1时，Jacobi椭圆函数退化为三双曲函数

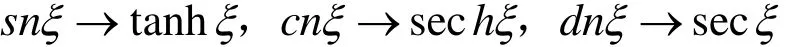
关于Jacobi椭圆函数更多的了解，可参阅[6,7]。

第二步：将(5)、(6)代入(4)，则可得到关于f(ξ)和g(ξ)的多项式；

第三步：令 fi(ξ) gj(ξ)的系数和在第二步得到的方程的常数项为0，则可以得到一个代数方程组；

第四步：对于 i +j=0,1,2,…n，解在第三步中得到的代数系统，而得到所设参数的值；

根据方程(5)、(3)而得到φ(ξ)和方程(2)的精确解。

本文主要讨论 (1)的精确解。首先做一个变换，假设：

将(7)式代入(1)式并整理其实部和虚部可得：

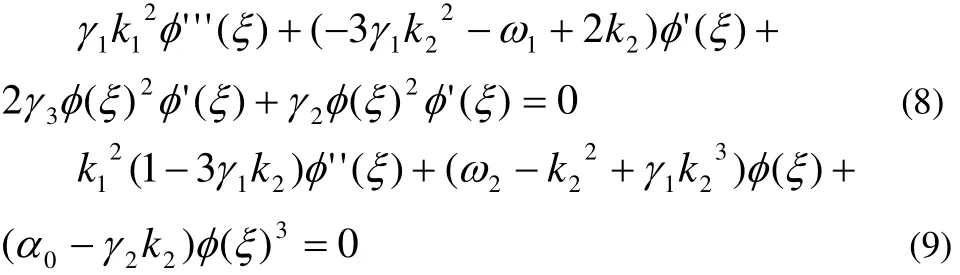
对(8)式两边关于ξ进行积分，且积分常数为0，则有：

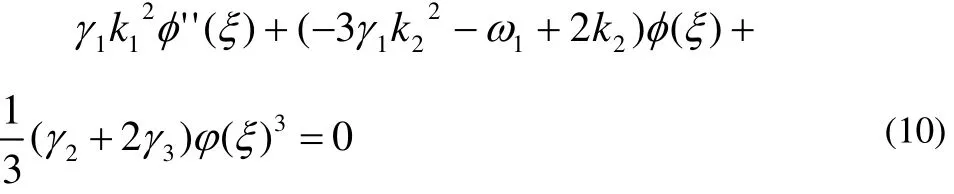
比较 (9)(10)式，它们有相同的解，则其系数应满足：

根据上式，可得：

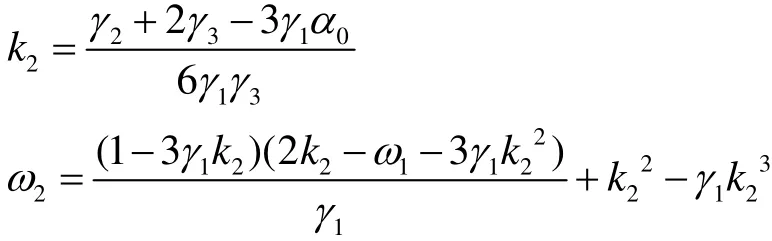
因此，可以将求解原方程(1)精确解的问题，转换为求解方程(10)的解。为了计算方便，令：

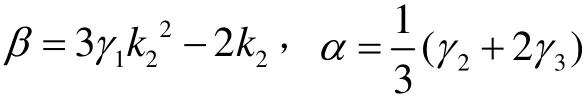
则方程(10)可以简化为：

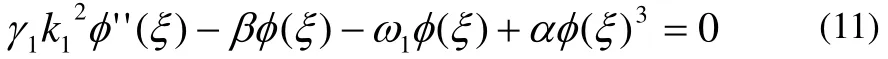
利用奇次平衡法，平衡φ''(ξ)和φ(ξ )3的次数，则可得τ =1。现在来寻找方程(11)具有以下形式的精确解：

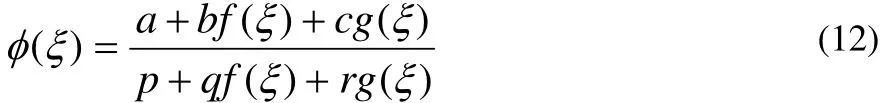
将方程(12)、(6)式代入 (11)，得到关于f(ξ)和g(ξ)的方程，令其系数及常数项为 0，可得一个关于a， b， c， r ，p， q ， k1， ϖ1的方程组，解其方程组可得以下主要结果：

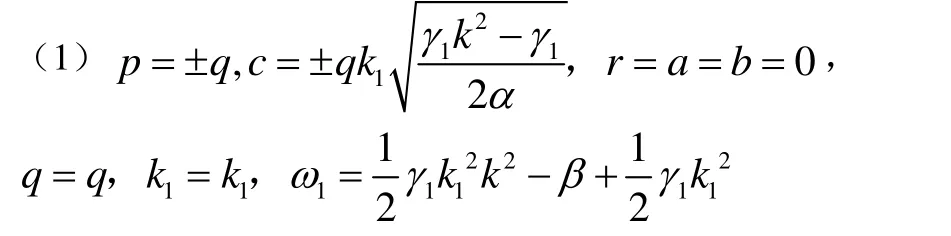
则当 αγ1( k2-1)＞0时，根据椭圆函数的性质有：

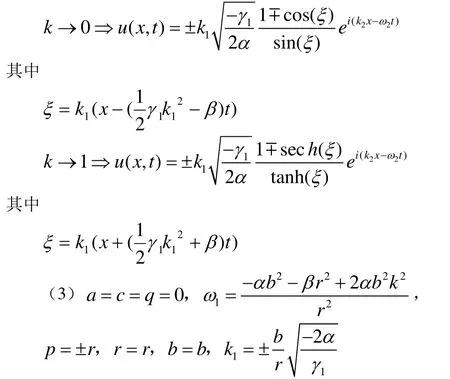
则当α γ1＜0时，根据椭圆函数的性质有：

则当α γ1＜0时，根据椭圆函数的性质有：

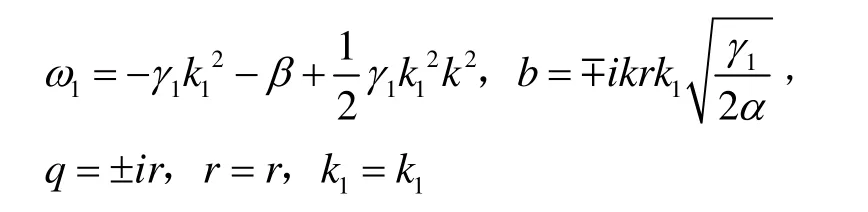
则当αγ1＞0时，根据椭圆函数的性质有：

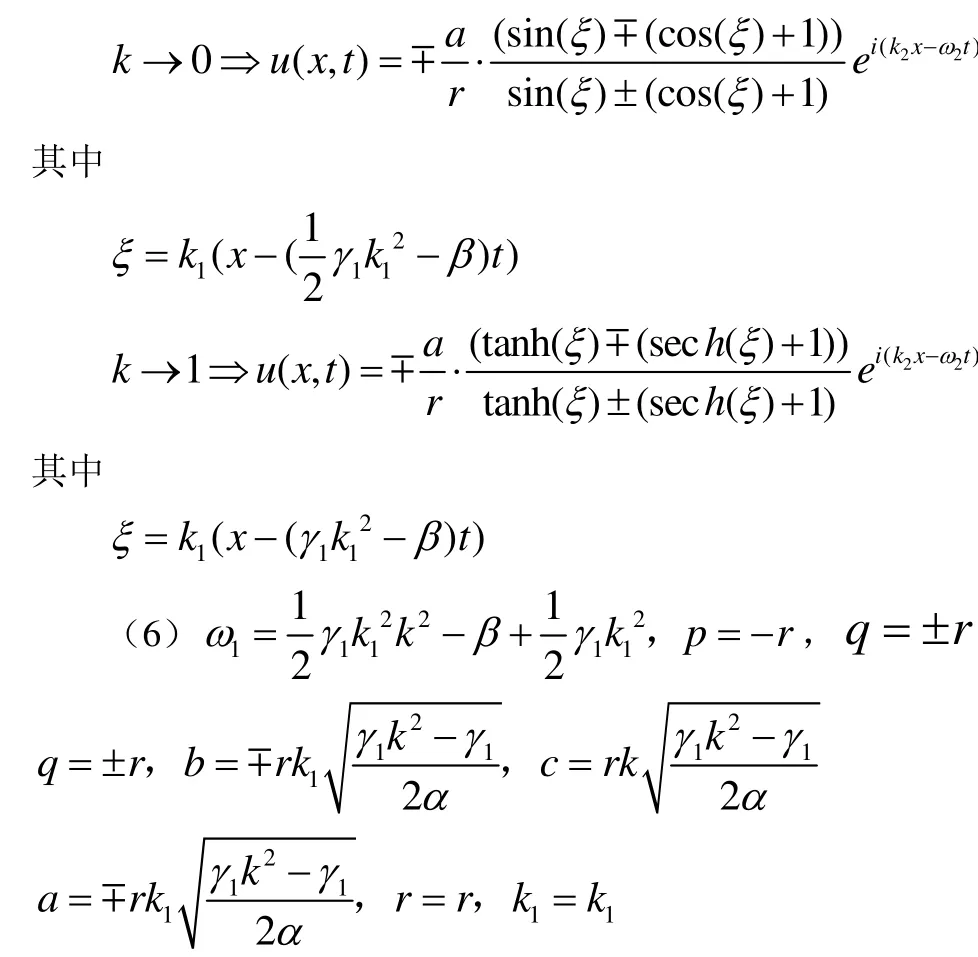
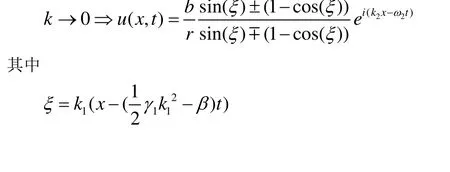
本文根据直接截断法及Jacobi椭圆函数的性质，得到了高次非线性薛定谔方程的新的 Jacobi椭圆函数解。可以看到，此直接法比已知的一般的方法对于得到一些具有特殊形式的精确解更直观且更有效。但是，如果方程不存在假设形式的解，此方法将无能为力。需要说明的是，此方法不但适用于其它非线性波动方程，对于解常微分方程也适用。