基于混沌量子进化算法的单交叉口信号控制*

徐山峰 蔡延光

（广东工业大学自动化学院）

1 引言

交通拥堵是城市发展过程中所面临的突出问题，交叉口信号配时优化对解决日益严重的交通拥堵问题起着至关重要的作用。本文针对区域交通单交叉口信号配时协同控制问题的特点，提出混沌量子进化算法（Chaos Quantum Evolution Algorithm，CQEA），以求解单交叉口信号配时协同控制的优化方案。大量的仿真计算表明，该算法具有较快的收敛速度和较强地获得最优解的能力。

2 单交叉口信号模型

以单交叉口四相位信号控制为例，信号控制示意如图1所示。交通流分为东、西、南、北4个方向，每个方向存在左转、直行和右转3个车道车流，对于右转车辆不实行控制。4个相位的交通流分别为东西直行、东西左转、南北左转、南北直行。任一时刻，只有一个相位的车流有权通过交叉口。本方案在信号周期固定的前提下，依据各车道车流量信息，以交叉口周期滞留车辆总数最少为目标，对各相位信号进行配时。

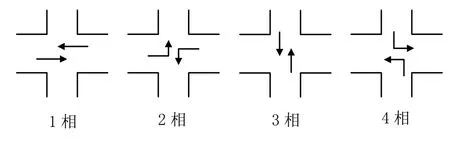
图1 交叉口相位图

为方便研究，对右行方向不实行控制。车道k（ k =1,2分别表示左行和直行车道）的车辆放行状态，用矩阵表示，其中i为相位编号；j为方向编号（ j =1,2,3,4分别表示东、南、西、北方向）：

设T为信号周期， xi(i=1,2,3,4)为一个信号周期内第i相位的配时时间；cijk表示第i相位、j方向、k车道的车辆到达率； gijk为绿灯期间内，第i相位、j方向、k车道车辆的离开率；表示第l( l=1,2,...)周期、i相位、j方向、k车道滞留的车辆数，则：

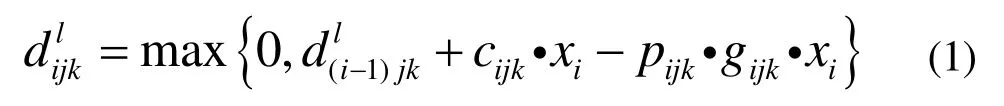
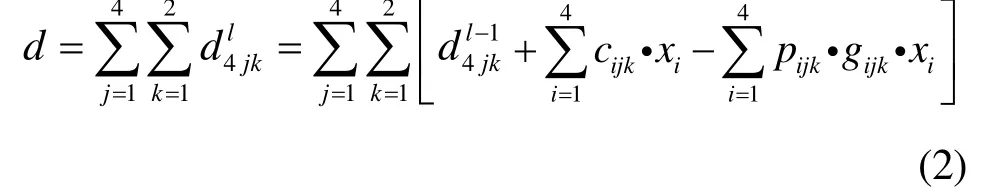
根据以上讨论，可得到单交叉口信号模型1：

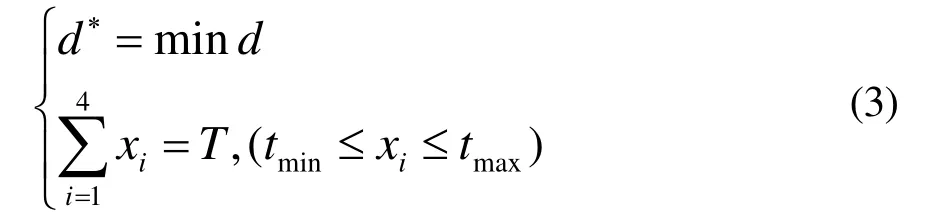
3 混沌量子进化算法

3.1 算法介绍

本文提出的混沌量子进化算法采用混沌初始化方法产生初始种群，利用混沌现象随机和不重复遍历的特性，使种群在可行解空间中形成比较理想的分布；采用量子旋转门更新当前种群中的非最优个体，引入混沌变异策略，利用混沌变异引导量子旋转门的旋转角大小及旋转方向，更新种群中的非最优个体，从而提高算法的寻优能力，克服早熟收敛。当前种群中的最优个体是指对应的目标函数值最小的个体。

3.2 染色体编码

考虑到二进制编码在优化高维度函数时为满足精度要求会增加编码的二进制位数，出现位数灾难等问题。针对交叉口信号配时问题，需要对编码进行改进，本文采用基于实数的编码方式。

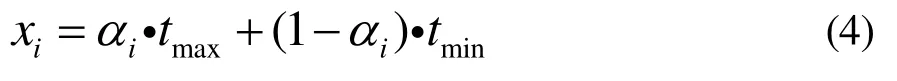
显然，αi与xi之间形成一一对应的关系。

3.3 混沌初始化

初始种群中任一个体的产生过程如下：

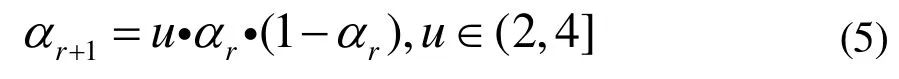
取u=4，此时系统完全处于混沌状态。αr的变化范围为初始种群中第i个个体编码对应为其中

3.4 适应度函数

适应度是区分群体中的个体好坏并对个体进行优胜劣汰选择的标准。本文采用轮盘赌选择法，先将Ψ按式(4)解码为模型1的配时方案再计算其所对应的适应度值 fi：

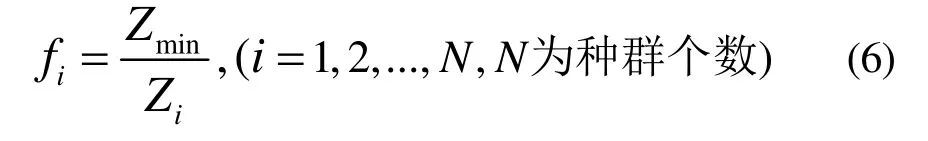
其中， fi为第i个个体的适应度；Zmin为当代种群中最优个体的周期滞留车辆总数；Zi为第i个个体所对应的周期滞留车辆总数。

3.5 混沌变异策略

本文采用混沌变异策略引导量子旋转门更新当前种群中的非最优个体。

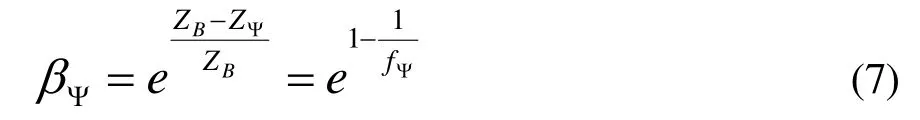
其中，ZB为当前最优个体的周期滞留车辆总数；ZΨ为当前种群中的任一非最优个体的周期滞留车辆总数；fΨ为个体Ψ的适应度值。

个体Ψ对应的第i个基因αi的旋转角Δθi：

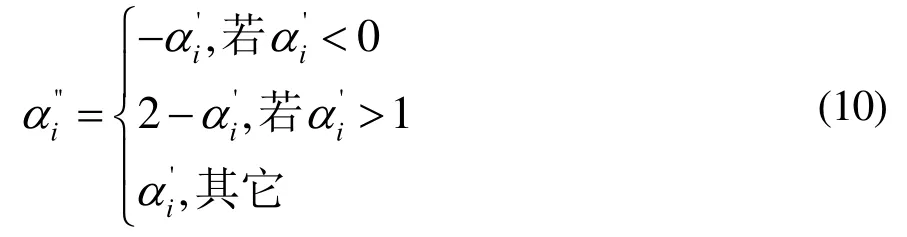
3.6 算法设计

基于以上讨论，得到求解模型l的混沌量子进化算法。

(1)初始化：

② 算法参数设定：设置种群规模N最大进化代数MG（正整数）；

③ 设置进化代数PG=0，按3.3节所述方法产生初始种群。

(2)对种群中的所有个体按式(4)解码得到对应的配时方案，按式(6)计算个体适应度值，找出当前种群中的最优个体。

(3)若 PG=0，置当前种群中的最优个体为全局最优个体B。

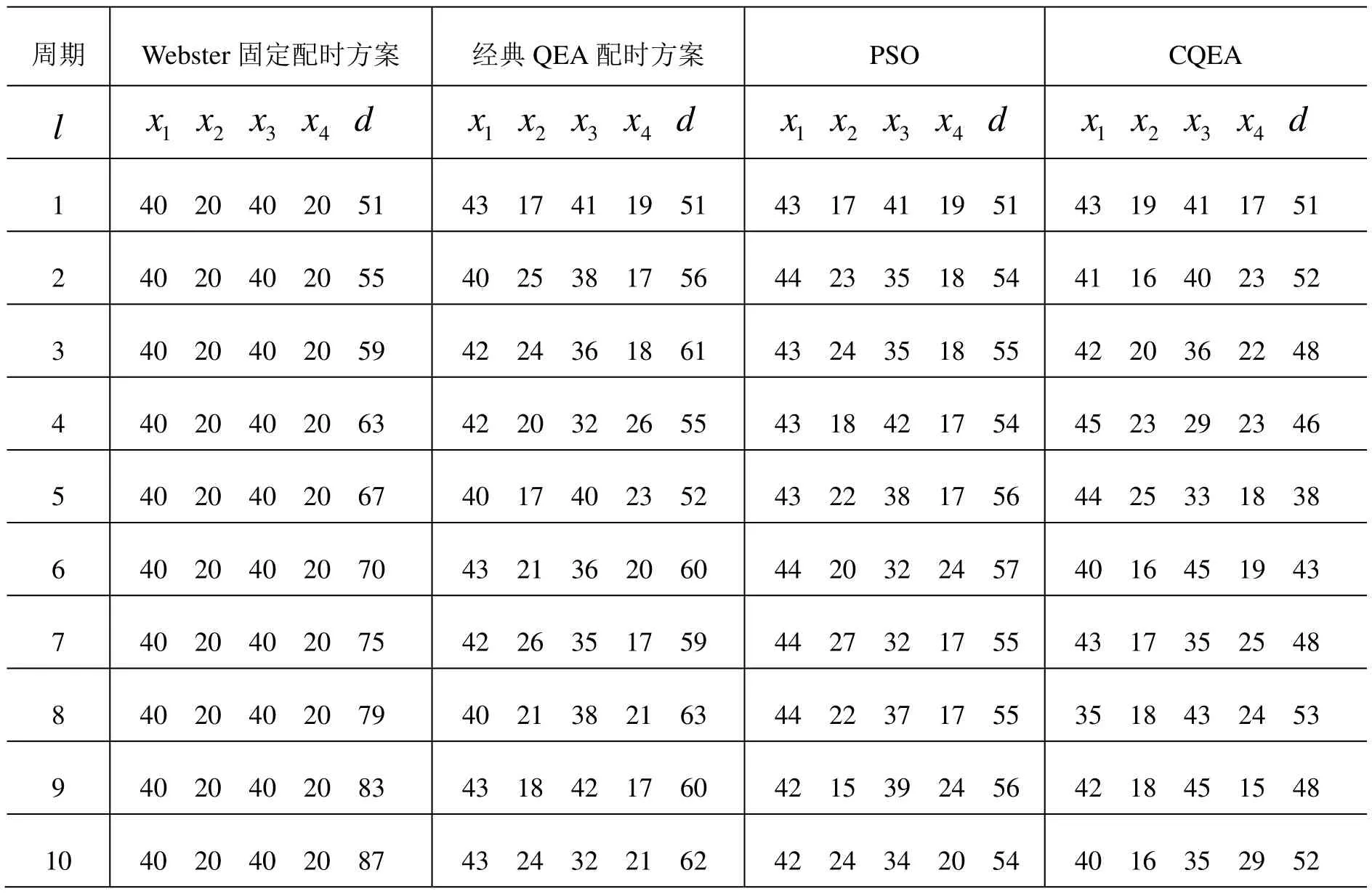
(4)若PG

(6)采用混沌变异策略诱导量子旋转门更新当前种群中的非最优个体。

(7)PG=PG+1，转(2)。

4 仿真分析

表1 四种配时方案的比较

从表1可以看出，采用Webster固定配时方案时，随着周期次数的增加，交叉口滞留现象趋于严重，通行效率急剧下降；经典QEA算法能够在一定程度上对信号进行配时，但容易陷入局部最优；PSO算法使各周期滞留车辆数保持在一个稳定的数据，有效缓解了交叉口拥塞；而与PSO相比，CQEA的总平均滞留车辆数明显减少，并且各周期滞留车辆数均较后者少，在种群规模方面，CQEA比PSO要小很多，从相位配时时间的周期性变化来看，CQEA很好的适应了各车道车辆到达率的变化，这表明CQEA有更优秀的搜索性能和迭代速度，并具有较强的获得最优解的能力。

5 结束语

本文在量子进化算法的基础上引入混沌变异，提出一种新的算法——混沌量子进化算法，并将其应用于单交叉口的信号配时。仿真结果证明了算法能够满足交通信号优化控制动态性和实时性的要求，优化结果对改善路口交通拥挤具有明显的效果。本文算法针对的是单交叉口4相位的信号配时优化，同样也可以扩展到更多相位及多交叉口的交通系统优化控制中。

[1]Cai Yanguang,Zhang Minjie. A hybrid chaotic quantum evolutionary algorithm [C]. 2010 IEEE International Conference on Intelligent Computing and Intelligent Systems,2010,2:771-776.

[2]魏明,蔡延光.一种基于混沌领域搜索的自适应混沌遗传算法[J].计算机应用研究,2009,26(2):464-465.

[3]夏学成,蔡延光,温金保.基于量子粒子群算法的单交叉口信号控制[J].工业控制计算机,2011,24(3):66-67.

[4]裴玉龙,孙明哲,董向辉.城市主干路交叉口信号协调控制系统设计研究[J].交通运输工程与信息学报,2004,2(2):41-46.

[5]郭海燕.基于混沌优化的量子遗传算法[J].电子测量技术,2006,29(2):14-18.

[6]刘建华,刘建伟.基于粒子群算法的城市单交叉口信号控制[J].系统工程,2007,25(7):83-87.