深弹舵机电动加载系统的滑模模糊自适应控制研究

刘子陵

（92060部队，辽宁大连116041）

1 引言

深弹舵机加载系统是深弹仿真试验系统重要组成部分，用于模拟深弹舵面所受到惯性力矩、阻尼力矩、干扰力矩和流体动力所产生的铰链力矩，全面检测和验证舵机系统在负载作用下的动态性能及控制精度的。同时，将全实物试验转化为实验室条件下的半实物预测性试验，达到了缩短研制周期、节约研究经费、提高可靠性的目的。

在加载的过程中，舵机运动引起的多余力矩会使系统的稳定性变差、频带变窄、加载灵敏度降低，而传统的控制方法很难满足系统的动态和稳态指标要求，更无法处理系统的不确定性和非线性。因此如何抑制多余力矩是设计舵机加载系统、改善加载系统控制性能的关键。

本文研制了一种以电动舵机为加载对象的电动加载系统，模拟深弹在水下航行时舵机受到的力矩。为了解决结构参数不确定性给等效控制器设计带来的困难，将滑模变结构与模糊自适应控制相结合，设计了新型滑模模糊自适应控制器。仿真实验表明，滑模模糊自适应控制方法不仅改善了加载系统的跟踪精度，而且消除了外界干扰、抑制抖振，具有很强的鲁棒性。

2 舵机电动加载系统的数学模型

舵机电动加载系统主要由承载舵机、加载电机、转矩传感器和角度传感器四部分组成，如图1所示。在加载系统中，加载电机输出轴与舵机之间接入用于测量舵机轴承受扭矩的传感器和测量舵机轴角位移的角度传感器，并通过连轴器将电机、舵机、传感器和角度传感器同轴连接。由于力矩电机具有参数稳定性好、控制灵活、响应快等优点，选择力矩电机作为加载执行电机，加载电机的驱动器由可逆直流PWM斩波器实现[1]。

图1 舵机电动加载系统结构框图

电动加载系统是一个双伺服系统，舵机按照位置指令运动，负载模拟器被迫跟随舵机运动，它们之间存在同轴连接的耦合。舵机的运动对加载系统来说是一种很强的时变位置干扰，是产生多余力矩的根本原因。因而舵机位置跟踪性能影响了加载转矩的控制效果。由图1所示的原理图可以得出电机的传递函数方框图如图2所示。

则转矩为输出的加载环节的开环传递函数为

Jm为电机电枢转子和负载折算到电机轴上的转动惯量；Bm为总阻尼系数；Ra为电枢回路总电阻；La为电枢回路总电感；Ke为电机反电动势系数；KT为电机转矩系数；TL为电机输出转矩；Kf为扭矩传感器的扭转角刚度。

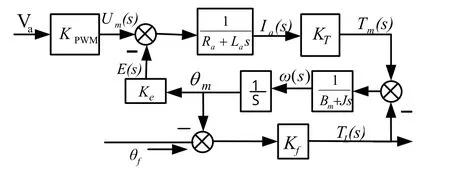
图2 舵机加载系统传递函数方框图

3 滑模模糊自适应控制器设计

3.1 常规滑模控制器设计[2]

以n阶非线性系统为例说明滑模控制器的设计过程，考虑如下n阶非线性系统

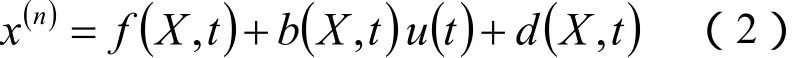
对该n阶非线性系统，根据滑模控制原理，选取如下形式的滑模面

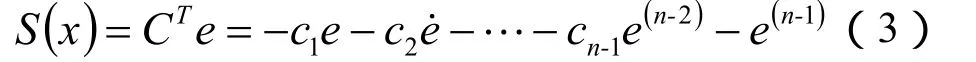
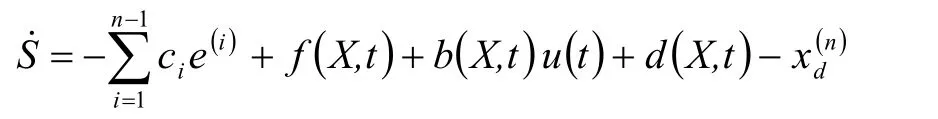
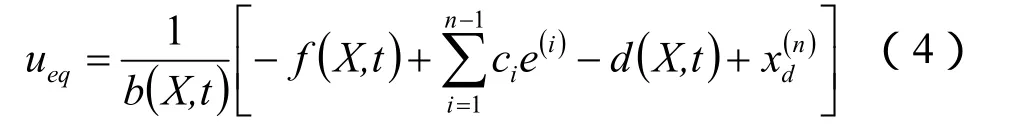
针对带有不确定性和外加干扰的系统，一般采用的控制律为等效控制加切换控制。即：u=ueq+uvss其中uvss实现对不确定性和外加干扰的鲁棒控制。为使滑模控制系统具有良好的动态品质，取

则滑模控制律设计为

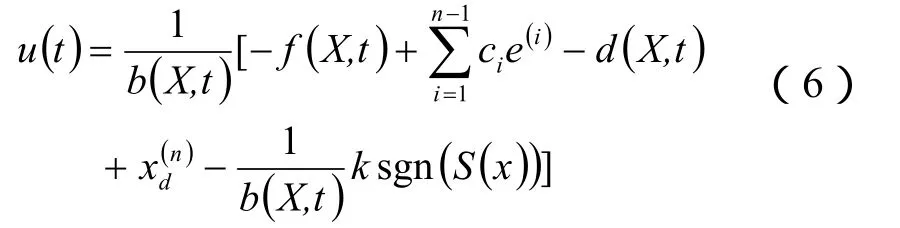
取李亚普诺夫函数为

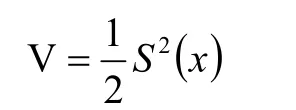
该系统在李亚普诺夫意义下是渐近稳定的。

3.1.2 滑模参数自适应控制器设计

由于电动加载系统中存在时变的不确定性，当这种不确定性已知时，应用滑模变结构控制可得到良好的鲁棒控制性能；但未知时，滑模变结构控制的性能会受到极大影响。实际上，系统中的函数f(X,t)，b(X,t)和干扰d(X,t)是未知的，因此控制律很难获得。通过自适应律对系统参数及外部干扰进行辨识，利用其的估计值代替其实际值来生成等效控制器[3]。如图3所示。

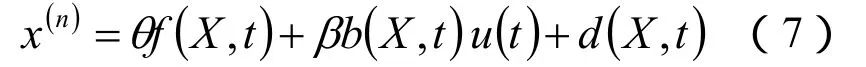
式中，θ、β为系统不确定参数。控制器取为

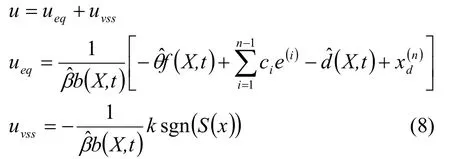
图3 舵机加载系统控制方案图

取李亚普诺夫函数为

将控制器（8）得

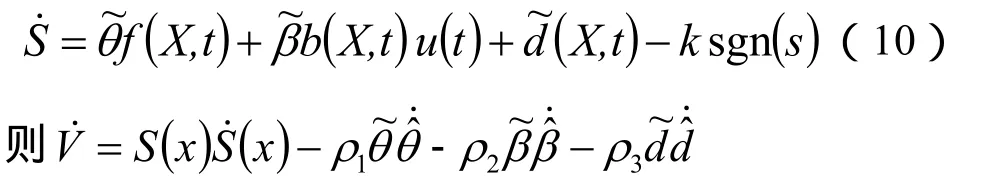
将式（10）代入上式得

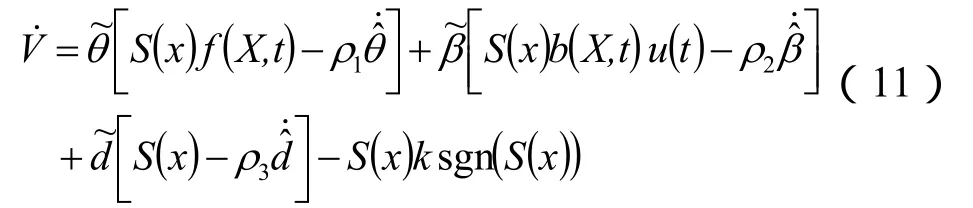
取自适应律为

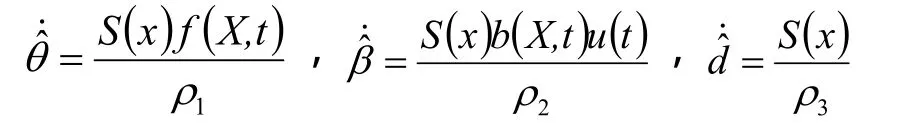
故系统在李亚普诺夫意义下是渐近稳定的。

3.3 滑模模糊自适应控制器设计[4、5、6]

滑模变结构控制可以通过控制器结构的不断调整和变化有效地控制具有参数变化和外部扰动的被控制对象，但是滑模变结构控制中用于处理不确定项的切换控制将使系统产生抖振现象。目前最常用的消除抖振方法是“边界层”法，但是边界层的引入将会降低系统的鲁棒性，而且边界层厚度的选择也是一个很困难的问题。鉴于此，本文在研究“边界层”法基础上，引入模糊控制理论采用组合控制方法来消弱抖振[7]。

1)“边界层”法

“边界层”法是用饱和函数sat(⋅)代替传统变结构控制中的符号函数 s gn(⋅)，起到了平滑切换的作用。则切换控制器变为

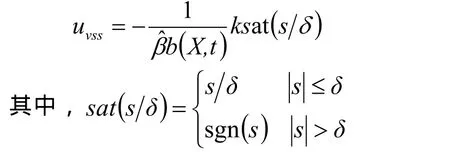
2) 滑模模糊自适应控制

在滑模控制中，为了保证被控系统的鲁棒性，控制增益k的取值应大于外界干扰与参数不确定上界的总和。然而外界干扰与结构参数是时变的，为了消除其影响，增益控制也应该是时变的，本文利用模糊系统来动态调节控制增益。

在调节控制增益的模糊系统中，以 ss˙作为输入变量，Δk作为输出变量，模糊控制规则设计原则为“if ss˙is a，then Δk is a”。定义变量 ss˙、Δk的语言值的模糊集均为：{NB，NM，NS，Z，PS，PB，PM}，论域分别为：{-20，-15，-10，-5，0，5，10，15，20}，{-2.0，-1.5，-1.0，-0.5，0，0.5，1.0，1.5，2.0}，隶属度函数均为正态分布函数，则控制增益模糊调节规则如表1所示。

表1 控制增益模糊调节规则表

采用中心平均解模糊的模糊系统，则

于是，k=k+αΔk，α为比例系数。

4 加载系统滑模模糊自适应控制仿真

采用上述滑模模糊自适应控制方法进行仿真，以验证该控制方法的有效性。选用电机参数为：Jm=0.2kg·m2；Bm=0.02N·m/A；Ra=8Ω；Ke=11.25 V·S/rad；KT=11.25N·m/A V·S/。仿真结果如图 4、5所示。其中，图 4中（a）、（b）分别为未采用控制器的系统阶跃响应曲线，跟踪力矩曲线，给定力矩载荷谱为 s in （1 0π t ）N·m；图 5 中（a）、（b）、(c)分别为采用控制器的系统阶跃响应曲线，无外界干扰下力矩跟踪曲线及有外界干扰下力矩跟踪曲线，给定力矩载荷 s in （1 0 π t）N·m，不确定性量0. 1 s in（10 π t）N·m， 给 定 舵 角 速 度 载 荷θ˙=5sin（10π t ）rads。曲线1为加载转矩的给定力矩，曲线2为加载系统输出跟踪转矩。

由系统的阶跃响应曲线图4（a）和图5（a）可以看出，滑模模糊自适应控制具有较快的跟踪响应，系统稳定时间由 t = 0 .2s降低为 t = 0 .08s，且具有较小的超调量。由跟踪力矩曲线图可以看出，滑模模糊自适应控制算法可以实现很好的跟踪精度，且具有很强的抗外界干扰能力。

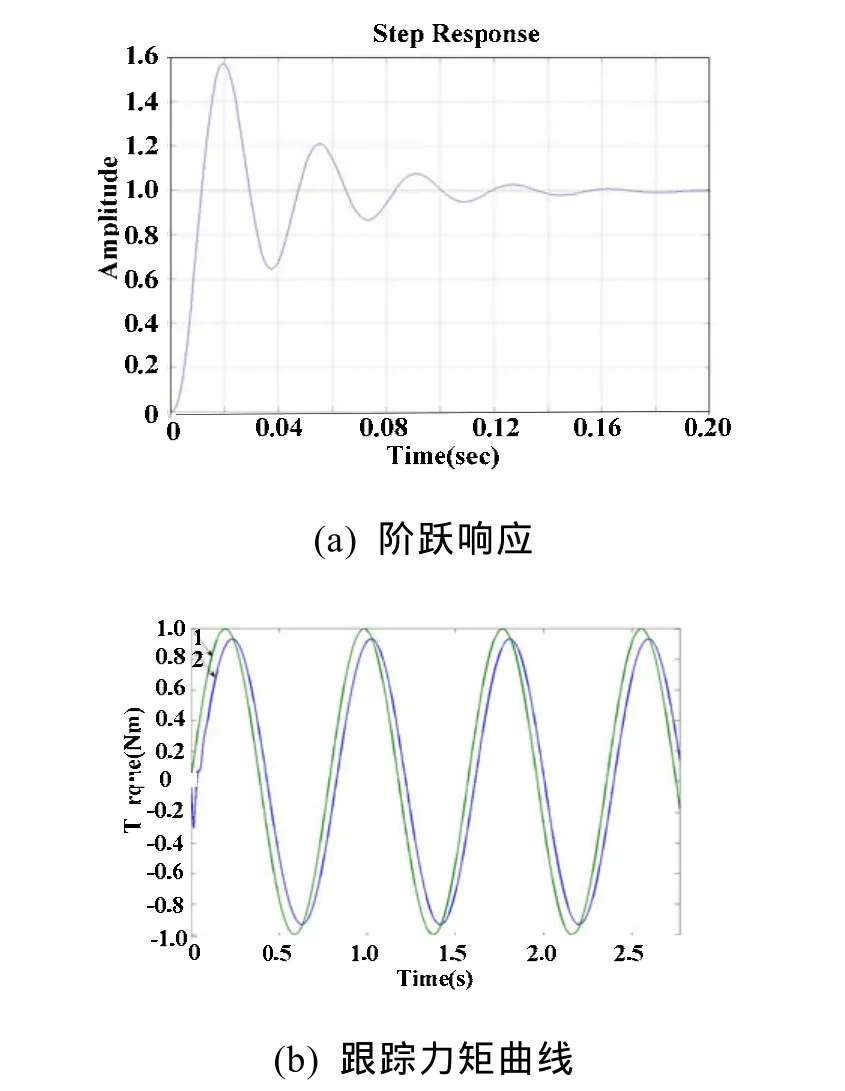
图4 未加控制器时的仿真结果

5 结论

本文对电动加载系统的滑模模糊自适应控制算法进行研究，仿真实验表明，滑模模糊自适应控制方法不仅改善了深弹舵机电动加载系统的跟踪精度，而且还有效地消除了外界干扰、抑制抖振，具有很强的鲁棒性。该建模与仿真是一种可行性方案，对舵机电动加载的进一步研究有一定的借鉴作用。

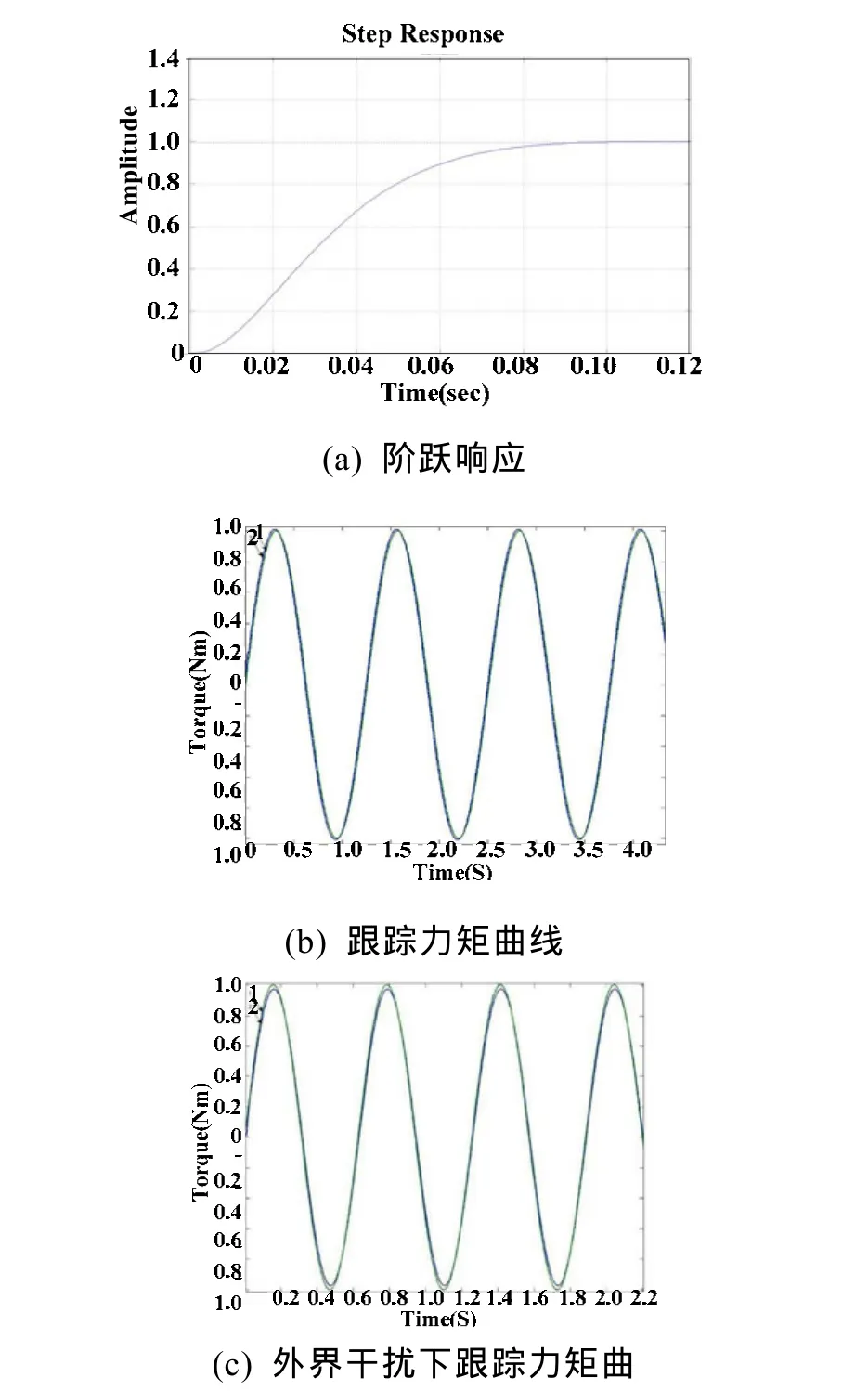
图5 滑模模糊自适应控制器仿真结果

[1]史晓娟. 一种基于神经元离散滑模变结构的位置控制方法[J]. 仪器仪表学报, 2008, 29(7)： 1559-1562.

[2]田宏奇. 滑模控制理论及其应用[M]. 武汉： 武汉出版社, 1995.

[3]董朝阳, 吴振辉, 陈宇等.直接力导弹的模型参考自适应滑模控制器设计[J]. 系统仿真学报, 2008,20(13)： 3500-3053.

[4]刘乔, 吴新跃, 石阳等. 电液伺服系统的积分滑模自适应控制方法研究[J]. 机床与液压, 2008, 36(5)：126-129.

[5]崔立超, 刘学忠. 模糊自适应滑模控制及其应用研究[J]. 德州学院学报, 2008, 24(2)： 53-56.

[6]周晓希, 黄辉先. 一种新型滑模控制器设计及仿真[J]. 计算技术与自动化, 2007, 26(4)： 41-25.

[7]刘伟, 张茂青, 王力等. 变结构控制系统的抖振问题[J]. 江苏电器, 2008, (5)： 1-2.