一种提高粒子群算法优化性能的方法

李承 许江宁 张文成

（海军工程大学导航工程系，武汉 430033）

0 引 言

粒子群优化算法[1]（PSO）是由 Kennedy与Eberhart于1995年提出的一种群体智能算法，用来模拟鸟群觅食的过程。PSO概念简单易懂，收敛速度快且代码实现容易，在优化及演化计算等领域引起许多学者的关注，成为一种解决非线性优化问题、组合优化问题与混合非线性问题等方面的重要优化工具和优化方法。针对粒子群算法本身存在的不足，学者们提出了很多改进方法[2-7]，通过引入惯性权重的概念，发展出来的标准粒子群算法成为最通用的一种。标准粒子群算法在函数优化、神经网络训练、模式分类和模糊控制等方面得到了广泛的应用，国内相关研究则始于2001年。

本文提出的利用算法的初始化策略提高算法的性能，并不改变算法的寻优策略和基本原理，因而对各种改进的粒子群算法有普适性。经实验仿真证明，该方法能够改善几种改进粒子群算法的寻优成功率和收敛速度，明显提高了算法性能。

1 标准粒子群优化算法概述

粒子群优化方法提出之后，有很多学者都对基本算法进行了大量的研究。针对粒子群算法容易陷入局部最优的问题，提出了很多的改进方法。Shi与Eberhart提出了带惯性权重的粒子群算法，此种改进方法被学者称为标准粒子群算法[2-4]（Standard Particle Swarm Optimization，SPSO），是目前粒子群算法研究和改进的基础。设一个D维目标空间，群体规模为 m，xi=(zi1,zi2,…,ziD)为第i个粒子的D维位置矢量，vi=(vi1,vi2,…,viD)为粒子i的D维速度矢量，pBesti是粒子当前最优位置，gBesti是群当前最优位置，SPSO算法的可表示为：

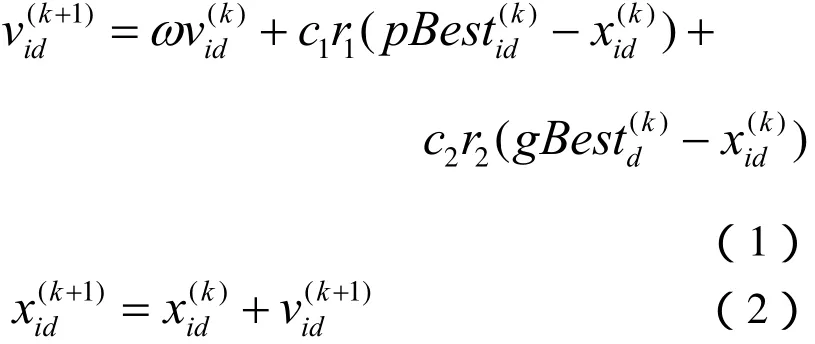
其中，i=1,2,…,m，d=1,2,…,D。惯性权重ω作为惯性部分，可以权衡算法全局能力和局部能力。r1、r2是[0,1]之间的随机数，用来保持群体的多样性。c1、c2被称为学习因子，代表粒子的自身部分和社会认知部分。

惯性权重的引入使粒子群算法的性能大大提高。SPSO算法的特点是原理简单，易于实现，需要调整的参数少，也不需要任何的梯度信息，特别是在非线性优化、组合优化和混合整数非线性优化上具有很大的优势。

2 几种改进的粒子群优化算法

2.1 线性递减惯性权重粒子群算法

Shi将惯性权重取值为常数，仿真结果表明，ω在[0.8，1.2]之间时，PSO 算法有更快的收敛速度，而当ω>1.2时，算法则较多地陷入局部极值。由于在一般的全局优化算法中，希望前期具有较高的全局搜索能力，而在后期有较高的开发能力，所以动态惯性权重随着算法迭代的进行而线性减小，算法的收敛性能得以改善。目前采用较多的惯性权重策略，是 Shi 建议的线性递减权值(linearly decreasing weight，简称 LDW)策略[1]。

式中，ωmax和ωmin是惯性权重的最大值与最小值；kmax和 k分别是最大迭代次数和当前迭代次数。惯性权重取值由式（3）给出，Shi等通过实验证明，将ω设置为从0.9到0.4线性下降，可以使PSO算法更好的控制全局搜索能力和局部搜索能力，加快了收敛速度，能够提高算法性能。目前这种惯性权重线性递减策略应用最为广泛，除此之外还有很多学者提出多种不同惯性权重策略，如线性微分递减策略、带阀值的非线性递减策略、非线性动态改进惯性权重策略、基于正切和反正切函数的惯性权重改进策略和模型调整ω的策略等，这些改进都使算法性能在不同方面有所提高。

通过调整惯性权重可以改进算法的性能，ω的大小决定了算法的全局搜索能力和局部搜索能力。ω较大则算法全局搜索能力强，ω较小则算法局部开发能力强，因此控制ω是改进算法的一种重要途径。

2.2 自适应惯性权重粒子群算法

APSO算法的基本思想是通过追踪粒子当前目标适应值和全局最优值，控制每个粒子的惯性权重。离当前最优解远的粒子获得的惯性权重值就大，从而加快粒子的飞行速度及算法的开拓能力；而离当前最优解近的粒子获得的惯性权重值就小，从而增加粒子的发掘能力。自适应惯性权重策略可由式（4）给出：

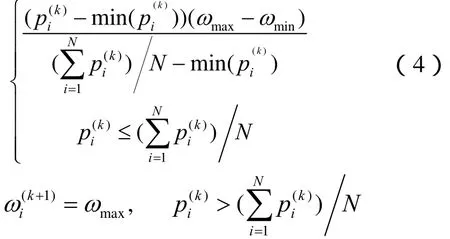
3 利用初始化提高算法性能

3.1 初始化策略

在对各种改进的粒子群优化算法进行大量实验测试过程中，发现了一些对算法寻优能力有影响的其他因素，比如粒子群位置的初始化和求解问题的维数。各种粒子群算法一般对粒子初始位置和速度没有特殊要求，但是在已知优化问题的搜索范围时，可以通过调整粒子初始位置和速度达到提高算法收敛速度的目的。

经过大量实验发现，对于限定搜索范围的优化问题，在粒子初始化时以位于搜索空间内的随机数对其初始位置赋值，这样既缩小了粒子起飞时到最优位置的距离，又保证了粒子群在搜索空间内充分发散，可以节约飞行时间，并提高寻优能力。因此，在已知算法搜索范围的情况下，本文用 xmax×rand()或者 xmax/2×rand()代替 randn()对粒子的初始位置进行赋值，用 vmax×rand()代替randn()对粒子初始化粒子速度。

3.2 实验验证

为了更好的反应粒子位置新的初始化策略对算法性能的影响，实验采用给定最大迭代次数和最优解的模式，以算法精确找到最优解为终止条件，执行测试算法。当达到最大迭代次数时或达到最大迭代次数前，算法找到最优解，则认为算法寻优成功。改进算法初始化策略的目的是提高算法的寻优能力，即算法搜索最优解的成功率、收敛速度和准确度。因此采用如下指标[8]：搜索成功率、平均迭代次数和平均最优适应值。

搜索成功率：进行T次实验，如果有t次实验成功，则成功率可表示为t/T×100%，此处所说的搜索成功是指成功搜索到精确解，不是表示算法的收敛概率。

平均迭代次数：T次实验中，所有成功实验迭代次数算术平均值。

平均最优适应值：T次实验所得目标函数最优值的算术平均值。

标准差：T次实验中算法所得最优解的标准差。

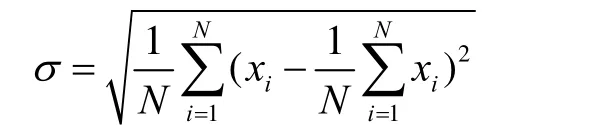
表示算法寻优结果的敛散性；选取一个典型单峰函数 Sphere函数和一个典型多峰函数 Rastrigrin函数，测试不同改进粒子群算法采用本文提出的初始化方法时的性能。

(1)Sphere函数

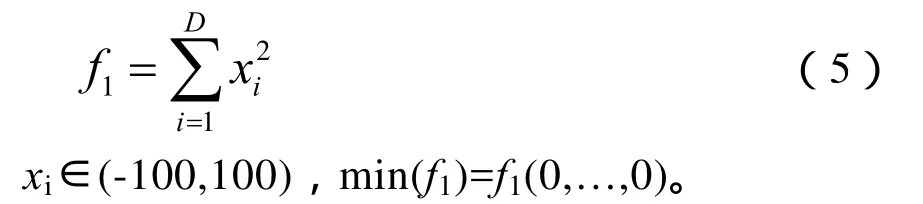
(2)Rastrigrin函数

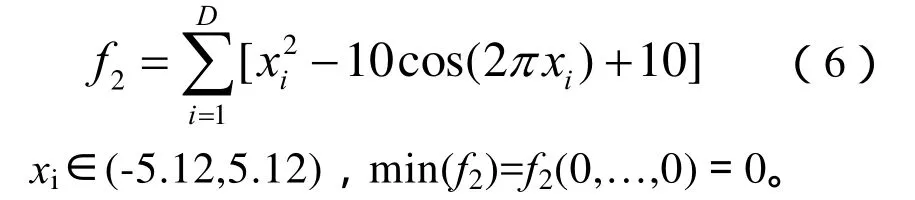
Sphere函数是非线性对称的单峰函数，不同维之间是可分离的。Rastrigrin函数是非线性多极值函数，存在大量按余弦排列的、很深的局部最优点。变量之间无任何相关性，其局部最优点随着余弦波动，很容易使算法陷入到局部最优点，而得不到全局最优解。

测试时不仿选取LWPSO和APSO两种算法，分别将其初始化策略改进前后的算法性能进行对比，进行 10次运算求平均值。令问题维度为D=20，种群规模M=30，最大迭代次数为N=2000，学习因子c1=2，c2=2，测试结果见表1。

为了更直观的反映不同算法的性能，图 1～图4分别给出了LWPSO和APSO算法初始化策略改进前后，对文中两个函数进行测试时的平均适应度值收敛情况（为了便于观察只给出了迭代早期变化明显的部分）。

图1和图2所示为LWPSO算法采用不同初始化策略时，对Sphere函数和Rastrigrin函数的寻优结果。

图3和图4所示为 APSO算法采用不同初始化策略时，对Sphere函数和Rastrigrin函数的寻优结果。

表1 Sphere函数测试结果对比

表2 Rastrigrin函数测试结果对比

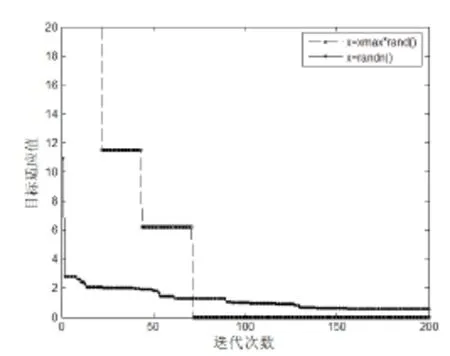
图1 LWPSO对Sphere函数的优化过程

图2 LWPSO对Rastrigrin函数的优化过程

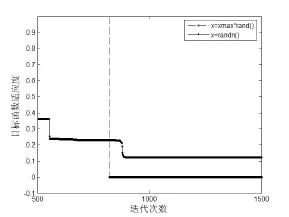
图3 APSO对Sphere函数的优化过程

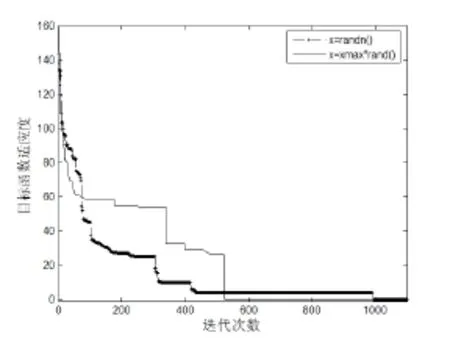
图4 APSO 对Rastrigrin函数的优化过程

由表1、表2和图1-图4的结果可以看出，在本文提出的算法初始化策略下，LWPSO和APSO算法对典型单峰函数和多峰函数寻优时，算法的收敛速度和搜索成功率，都得到了大大提高。

4 结论

本文针对解决控制领域优化问题的粒子群算法存在的问题，提出了一种算法的初始化策略，以提高优化算法的性能。通过 LWPSO和 APSO算法对典型函数的测试，结果证明在本文提出的初始化策略下，算法收敛速度、搜索成功率和搜索精度得到了大大提高，这说明本文提出的方法是有效的。

[1]纪震，廖惠连，吴青华. 粒子群优化算法及应用[M].北京: 科学出版社, 2009:16-80.

[2]Zhang L P,Yu H J, Hu S X. A new approach to improve particle swarm optimization [C]. Lecture Notes in Computer Science. Chicago: Springer Verlag,2006: 1036-1043.

[3]邓爱萍，王会芳. 动态改变惯性权重的自适应粒子群算法[J]. 计算机工程与设计, 2010, 31(13):3062-3065.

[4]潘峰,陈杰,甘明刚等. 粒子群优化算法模型分析[J].自动化学报, 2006, 32(3): 368-377.

[5]林川,冯全源. 粒子群优化算法的信息共享策略[J].西南交通大学学报, 2009, 44(3): 437-441.

[6]张朝龙，江巨浪，江善和等. 一种自适应混合粒子群优化算法及其应用[J]. 计算机应用研究, 2011,28(5): 1696-1698.

[7]张顶学. 遗传算法与粒子群算法的改进及应用[D].武汉：华中科技大学， 2007.

[8]F V den Bergh, A P Engelbrecht. A study of particle swarm optimization particle trajectories [J]. Inf. Sci.,2006, 176(8): 937-971.