基于PSCAD的异步电动机直接转矩控制仿真

裴峰 姜晓弋 魏建勋

(1.中国人民解放军海装沈阳局，沈阳 110031；2.海军工程大学电气工程系，武汉 430033；3.湘电集团有限公司，湘潭 411101)

0 引言

1977年美国学者A.B.Plunkett在IEEE杂志上首先提出了直接转矩控制理论，1985年由德国鲁尔大学Depenbrock教授和日本Tankahashi分别取得了直接转矩控制在应用上的成功[1]。直接转矩控制技术与矢量控制技术都属于交流电机高性能控制技术。直接转矩控制技术避免了复杂的解耦运算，采用定子磁链定向和瞬时空间矢量理论，具有控制算法简单，转矩响应速度快的优点，而矢量控制存在计算过程复杂、受电机参数变化影响大等问题。直接转矩控制技术控制思想新颖，结构简洁，动、静态性能优良，近些年来得到了普遍的关注和迅速发展。

本文在理论分析直接转矩控制系统结构的基础上，利用 PSCAD/EMTDC 软件搭建了异步电动机直接转矩控制系统仿真平台，并对其动态性能进行仿真，给出了仿真结果。

1 直接转矩控制的基本原理

1.1 异步电动机的数学模型[2]

异步电机在定子坐标系上的电压方程为：

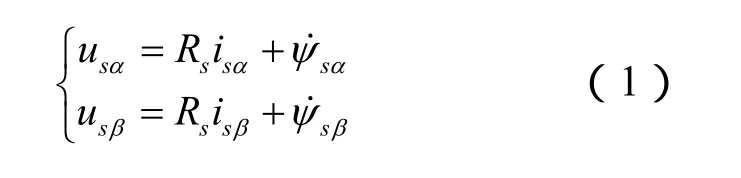
其中，下标 α、β分别表示对应空间矢量的 α分量和β分量。

移项并积分可得定子磁链公式：

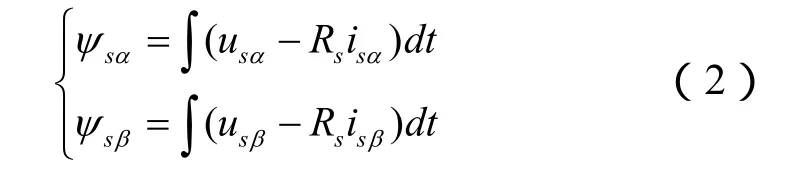
转矩公式：

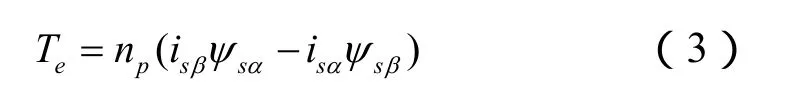
或

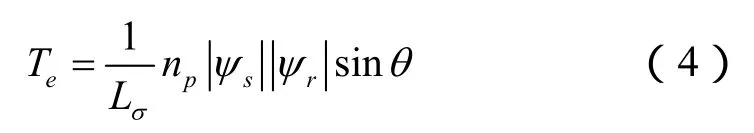
式中：Te—电磁转矩（N·m）；np—电机极对数；θ—磁通角（rad）。

电机运动公式：

式中：TL—负载转矩（N·m）；J—转动惯量（kg·m2）。

1.2 直接转矩控制的基本结构

直接转矩控制根据定子磁场定向原理，采用滞环调节器选择最佳的开关信号，直接对逆变器的开关状态进行控制，以获得转矩的高动态性能。直接转矩控制调速系统结构如图1所示。整个控制系统由磁链环、转矩环和速度环构成。通过检测异步电动机输入电压和电流，经3/2坐标变换得到两相定子坐标系下的电压usα、usβ和定子电流isα、isβ，通过磁链模型、转矩观测器计算出磁链和转矩，分别与磁链和转矩指令值进行比较，差值分别经磁链、转矩滞环比较器输出后经PWM控制信号生成模块产生逆变器的控制信号。其中，转矩给定是通过对转速偏差进行PI调节后得到的。

图1 异步电动机直接转矩控制系统结构图

理想电压型逆变器模型原理图如图2。上下桥臂的开通和关断状态互补，逆变器共有8种开关状态，包括六个工作状态，两个零开关状态。

交流调速系统通过控制逆变器改变电动机的动态过程，归根结底还是控制逆变器的开关状态，即在八种开关状态中选择最合适的一种作为控制器输出。由于定子电压与定子磁链之间存在微分关系，电动机旋转磁场的轨迹问题就可转化为电压空间矢量的运动轨迹问题。而根据式（4），转矩与定子磁链幅值、转子磁链幅值和磁通角θ有关。因此在实际运行中，在保持定子磁链幅值为额定值的同时，转子磁链幅值由负载决定，要改变电动机转矩，可以通过改变磁通角θ来实现。

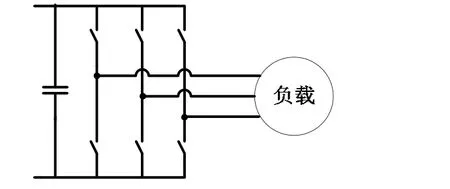
图2 理想电压型逆变器模型原理图

直接转矩控制通过空间电压矢量来控制定子磁链的旋转速度，以改变定子磁链的平均旋转速度，从而改变转差即磁通角θ的大小来控制电磁转矩[3-5]。

本文采用由式（2）确定的异步电动机u - i模型观测定子磁链，在计算过程中只需知道电动机的定子电阻 Rs，结构如图3所示。u - i模型用可以足够精度检测出来的定子电压 us( t)与定子电流 Is( t)，实现起来非常简单。该模型在30%额定转速以上时，能够较准确的确定定子磁链，而且结构简单，鲁棒性强[2]。

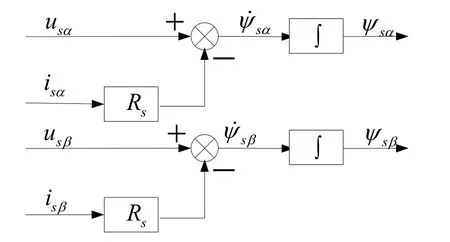
图3 定子磁链u - i 模型

2 基于 PSCAD/EMTDC 的 DTC 系统实现

PSCAD/EMTDC被广泛应用于电磁暂态仿真，EMTDC是一种具有开放式结构的电力系统暂态过程和电力系统控制方法的时域仿真程序。图4为直接转矩调速系统仿真模型。

在实际应用中，可检测的异步电动机线电压和线电流都是基于三相静止坐标系的，因此需要利用 Clark坐标变换将三相坐标系统中的各个量转换到静止两相坐标系中。Clark变换矩阵如式（6）示，其PSCAD自定义模型如图5所示。

直接转矩控制系统的逆变器开关状态选择测量如表 1所示，PWM控制信号生成模块的自定义模型如图6所示。

其中，SF为磁链滞环比较器输出的磁链控制信号，ST为转矩滞环比较器输出的转矩控制信号，SS（1，2，··，6）为定子磁链所在的扇区[6]。

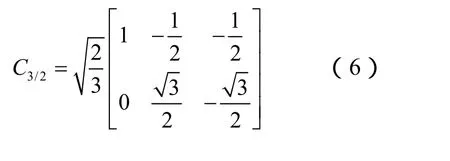
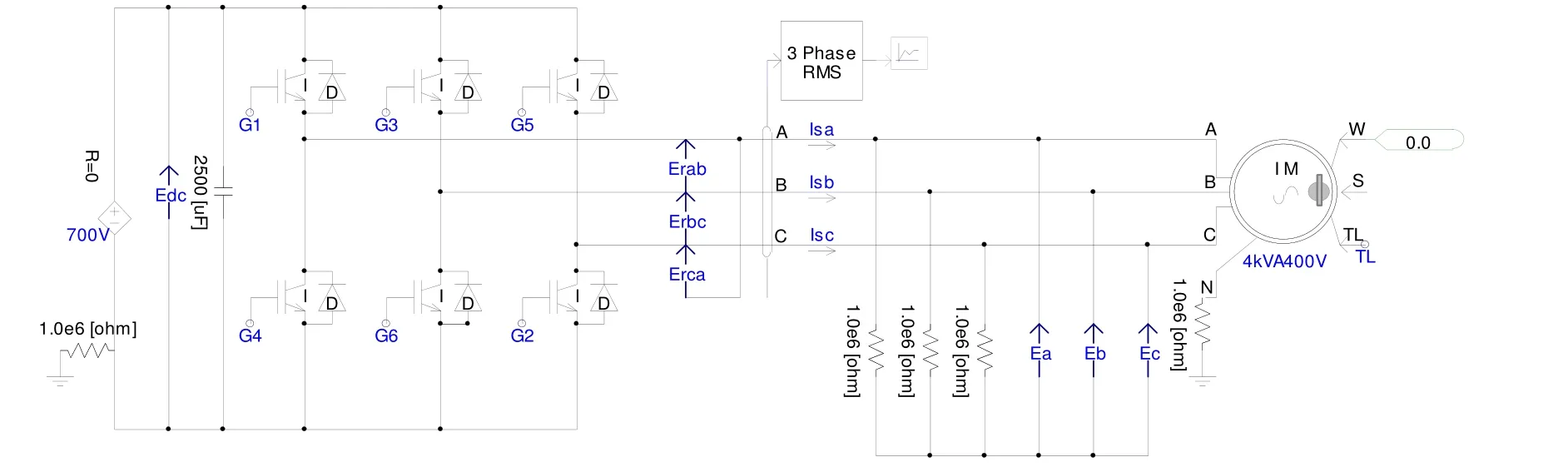
图4 直接转矩调速系统PSCAD仿真模型

图5 Clark变换的PSCAD自定义模型

图6 PWM控制信号生成模块的自定义模型

3 仿真结果分析

仿真中采用了电动机的标幺值系统。主要仿真参数为：直流电源电压700 V，异步电动机视在功率4 kVA，定子电阻标幺值0.03513，额定电压400 V，额定频率50 Hz，极对数2。

转速给定值如式（7）所示。 t = 1 s时刻，突加转矩为0.589（标幺值）的负载。

表1 传统直接转矩控制系统开关表

仿真波形如图7、8所示所示。其中ωref为转速指令值，ωrotor为电机转速；Te_given为转矩指令值， Te_obsv为电机转矩观测值； isa、 isb、 isc为定子电流。图8为定子磁链的轨迹图。

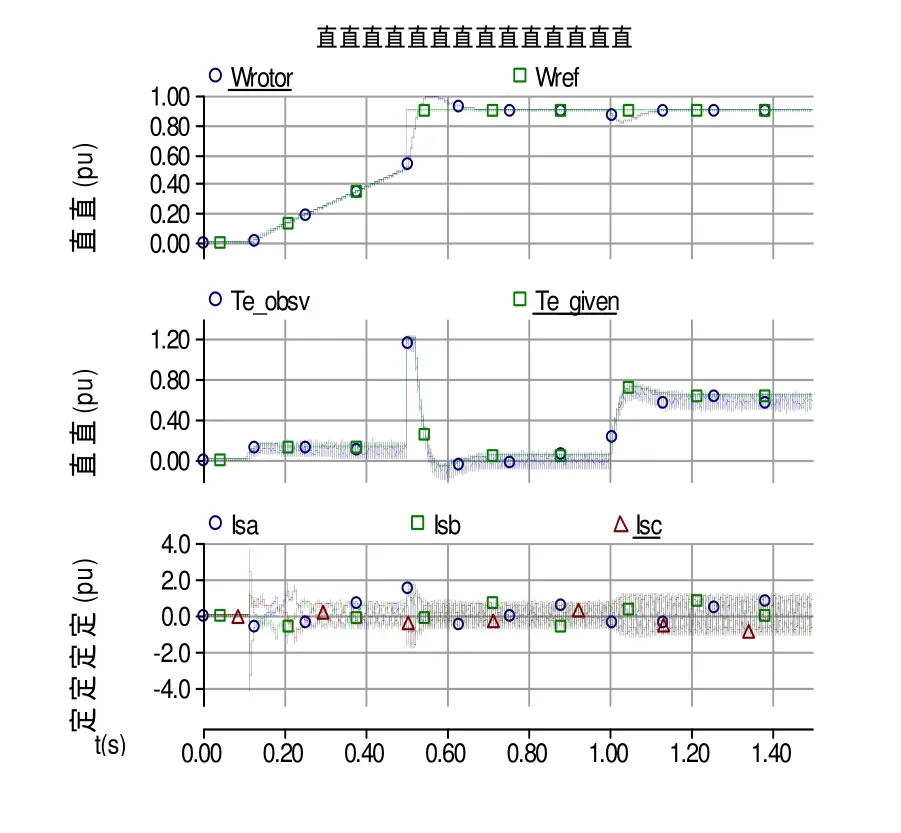
图7 电动机转速、转矩、定子电流仿真波形

由仿真结果可知，直接转矩调速系统中能够很好的跟踪转速指令值，转矩响应快速，定子磁链轨迹呈圆形，电动机电流波形平滑，调速性能良好。

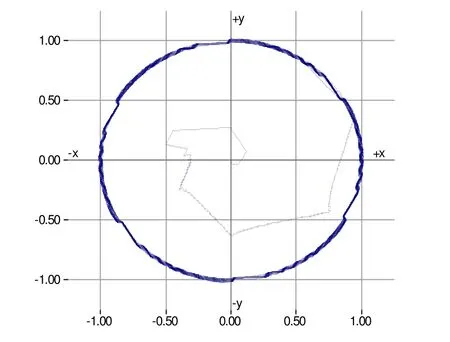
图8 定子磁链轨迹仿真波形

4 结束语

本文利用 PSCAD/EMTDC 软件研究了直接转矩控制系统的动态性能。仿真结果验证了仿真模型的正确性，也表明了直接转矩控制系统优良的调速性能。

[1]Giuseppe S. Buja，M P. Kazmierkowski.Direct torque control of PWM inverter-fed AC motors-A survey[J].IEEE Trans. and Electron, 2004, 5(4)： 744-757.

[2]陈伯时. 电力拖动自动控制系统[M].北京： 机械工业出版社, 2003.

[3]张俊喜.异步电动机直接转矩控制系统研究[D].哈尔滨： 哈尔滨理工大学, 2007.

[4]L. Tan, M. F. Rahman.A new direct torque control strategy for flux and torque ripple reduction for induction motors drive by using space vector modulation[J].Proc. 32nd Annu. PESC, 2001, 3：1440-1445.

[5]岳舟, 谭甲凡.直接转矩控制定子磁链观测新方法[J].电力电子技术, 2010, 44(11)： 60-63.

[6]陈特放, 刘子建. 基于MATLABISIMULINK的异步电动机直接转矩控制系统的建模和仿真[J].机车电传动, 1998(2)： 7-11.