综合粗糙集和修正熵权的数据融合系统性能评估模型
王振兴, 冯新喜, 鹿传国, 孔云波
(空军工程大学电讯工程学院,西安 710077)
0 引言
信息融合技术增强了系统的生存能力和战术性能,在军事领域得到了广泛应用。各种数据融合算法的出现,给数据融合系统的研制和开发提出了新的挑战。如何评测纷繁芜杂的数据融合算法为数据融合应用系统的工程实现提供决策支持,已成为数据融合领域研究的热点之一[1]。然而信息融合系统所汇集和处理的信息种类繁多,信源间关系复杂,应用背景和建设目标差异较大,使得客观、公正地评估融合系统性能较为困难。
为实现数据融合系统性能的客观、精确的评估,结合数据融合的算法流程,建立了一种多级、多层的数据融合系统的指标体系,同时为克服主观性对指标赋权的影响,采用粗糙集和修正熵权理论提出了一种针对数据融合系统性能的综合评估模型,并通过实例证明了该评估模型的有效性。
1 数据融合系统指标体系
建立科学合理的指标体系是进行有效评估的前提,数据融合系统性能评估指标体系的建立目前主要有两种模式:1)基于融合处理的流程划分,系统分析航迹起始、点-航迹关联、目标跟踪、航迹关联等各环节中的诸因素,分层建立指标体系[2];2)基于整个系统的功能需求,从系统的融合性能、时间性能、稳定性能等方面进行分析,构建指标体系[3]。二者基本特点是二级指标基本为定量指标,需通过大量的实验仿真得到基于统计学的精确数值,而一级指标在物理意义上的重要性区分较为明显,在特定的应用背景下功能需求差异也很大,比如在第一种指标建立模式下,航迹起始环节在整个融合处理流程中显然最为重要,直接影响之后的处理流程,融合精度重要性最低;而在第二种指标建立模式下,融合性能在系统各类功能需求中明显占首要地位,时间性能次之,因此对一级指标需要进行定性和定量相结合的综合评估。本文按第一种模式引入以下指标体系[4],如图1所示。

图1 数据融合系统指标体系Fig.1 Index system of data fusion system
2 综合粗糙集和熵权的评估模型
当前在工程数学领域比较成熟的评估方法有很多,主要可以分为3类:1)侧重于主观因素的量化分析,如主成分分析法、层次分析法等;2)侧重于挖掘指标数据本身的内部信息,如熵权法、粗集理论等;3)上述两种方法的综合运用,力求对主客观因素的综合考虑。虽然第三种算法兼有前两种算法的优势,但往往消弭了指标体系不同层次定性和定量程度的差异,因此也难以对数据融合系统性能进行全局评估。本文针对数据融合系统性能评估的自身特点,借鉴多模型混合评估法的思想[5],综合运用粗糙集理论、熵权法和层次分析法建立一种混合多层综合评估模型。
2.1 基本思想
粗糙集理论是一种刻画不完全性的数学工具,其特点是将知识理解为对数据的划分,仅依赖于原始数据而不需要任何先验信息便可揭示数据内部潜在的规律[6]。其权重确定思想是从属性集中去掉某属性后,计算分类的正域受影响的程度,是从决策分类的角度对属性重要性的一种度量。熵权法[7]是度量系统状态不确定性的一种方法,运用熵值原理确定的熵权系数,反映了在给定风险因素集和评判集后,专家的各种评价指标确定的情况下,各指标在竞争意义上的相对激烈程度,具有客观性强、数学理论完善等优点。因此对于定量型的二级指标,综合采用两种方法,从两种不同角度进行综合评估,以增强指标数据信息挖掘的可信性和有效性。而对于定性定量相结合的一级指标,拟引入决策者的主观经验,采用AHP方法[8]确定各指标的主观权重,继而修正熵权,将主、客观权重结合确定一级指标综合权重,最终由各级指标的综合权重得到系统性能综合评估值,其具体过程参见图2。
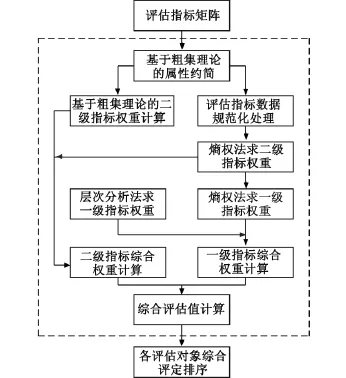
图2 综合粗糙集和熵权的评估模型Fig.2 Evaluation model of data fusion system combined rough set with entropy weight
2.2 基本流程
设有m个数据融合系统组成评估对象o1,o2,…,om,及 n 个一级指标 V1,V2,…,Vn,各一级指标下辖若干二级指标,用vij表示,共同构成多层次多属性决策评估系统。
2.2.1 二级指标约简和粗集权重
设对一级指标Vi,利用粗集理论进行属性约简和权重计算,得 Vi'=(vi1,vi2,…,viti),对应的权重向量为 Si=(si1,si2,…,siti),ti为一级指标 Vi经属性约简后所剩属性的个数,具体方法参照文献[5],这里不再赘述。
2.2.2 建立评估矩阵
根据上步所约简的指标,确定一级指标下的评估矩阵

2.2.3 数据归一化
为了消除不同性质指标间量纲和数量级的影响,需对指标进行规范化处理,将其规范化为[0,1]区间的极大型指标。
对于极大型指标,有
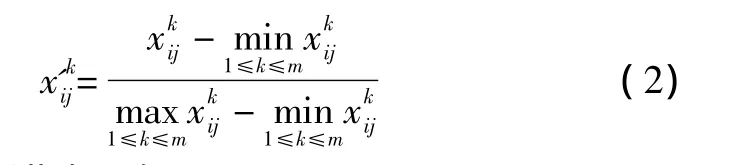
对于极小型指标,有

标准化公式为
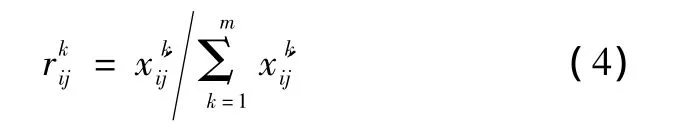
2.2.4 指标熵权
按照归一化熵公式,二级指标vij的熵、偏差度和熵权分别为
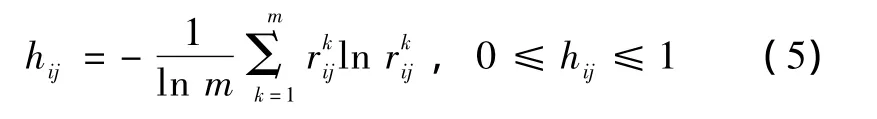
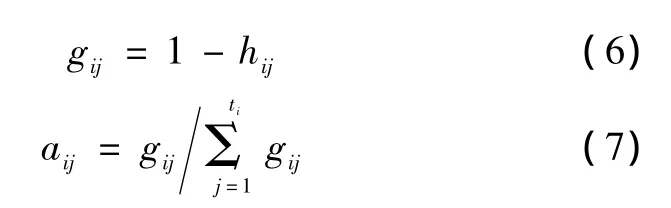
根据信息熵的可加性,一级指标Vi的偏差度为

则一级指标熵权

2.2.5 一级指标主观权重
层次分析法的基本原理是对指标间相互比较的重要性进行量化,一般采用1~9及其倒数的指数标度法构造判断矩阵,然后进行权重计算和一致性检验,具体方法参照文献[7],这里也不做深入探讨。设一级指标的 AHP 权重向量 E 为[e1,e2,…,en]。
2.2.6 指标熵权修正
二级指标的修正熵权为

一级指标的修正熵权为
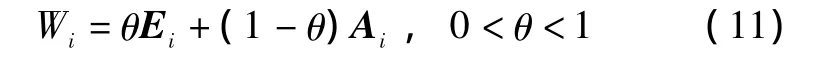
其中:θ为主观权重的可信度,由专家赋值。
2.2.7 确定综合权重
第k个评估对象的综合评估值为
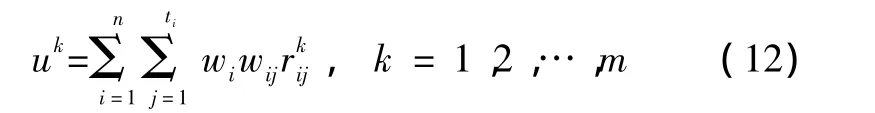
各评估对象的综合评估向量 U为[u1,u2,…,um],根据uk的值即可对评估对象综合性能进行优劣排序,高值为优,低值为劣。
3 应用实例
为了说明该方法使用步骤,现假设有某7种类型数据融合系统,采用本文提出的评估模型对其进行性能排序。因篇幅所限,各指标名称依次以字母代替,指标数据如表1所示。
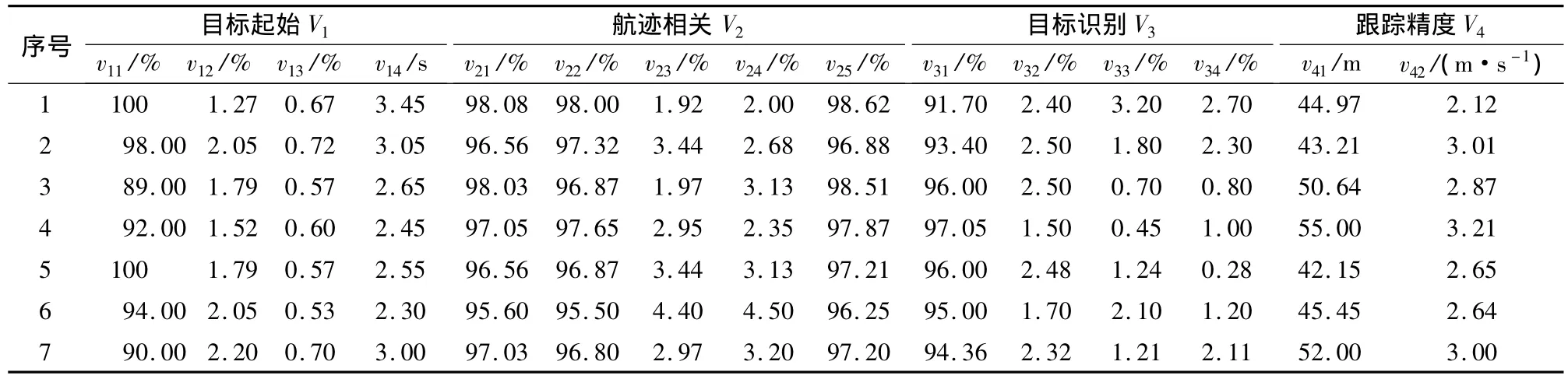
表1 数据融合系统评估指标数据Table 1 Values of the criterions for data fusion system
利用粗糙集得到的权重分别为
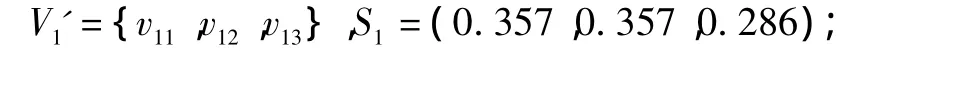
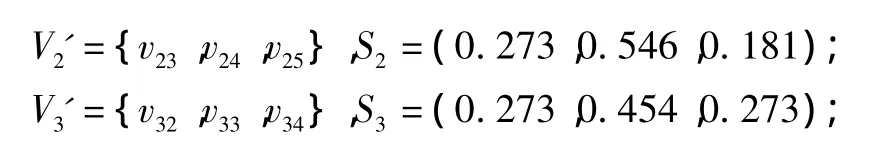
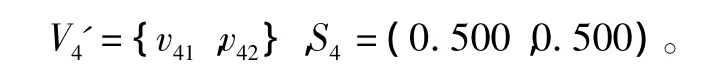
按式(1)~式(4)得指标数据标准化矩阵为
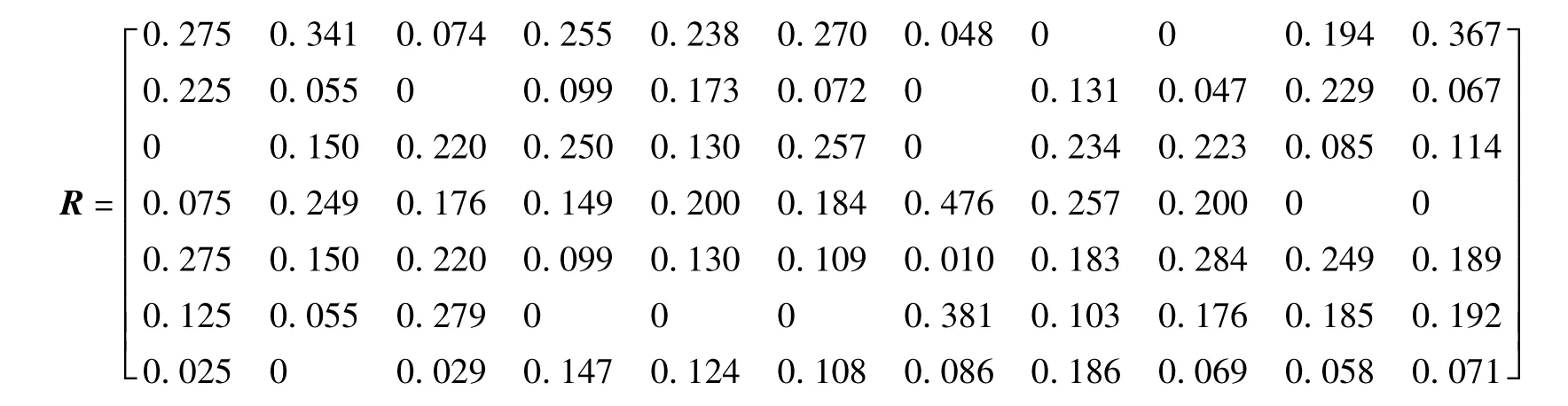
由式(5)~式(7)计算各二级指标的熵权向量为A1=(0.353,0.326,0.305),A2=(0.337,0.279,0.384),A3=(0.657,0.107,0.237),A4=(0.599,0.401)。
由式(10)可得各二级指标的修正熵权向量为W1=(0.355,0.341,0.296),W2=(0.313,0.436,0.243),W3=(0.313,0.390,0.289),W4=(0.550,0.450)。
由式(8)、式(9)可得各一级指标熵权向量A为(0.286,0.183,0.340,0.191)。
根据一级指标重要性的专家排序:航迹起始>航迹相关>目标识别>融合精度,计算AHP权重向量E为(0.580,0.256,0.114,0.050)。
简便起见,取主观权重可信度θ为0.5,由式(11)可得,一级指标修正熵权 W 为(0.433,0.220,0.227,0.120)。
由式(11)可得7个数据融合系统综合评估向量U为(0.193,0.104,0.140,0.180,0.180,0.134,0.071),根据评估值得出优劣次序为:1>5=4>3>6>2>7。
为进一步提高评估结果可信度,就θ的取值对评估结果影响进行观察,结果如表2所示。
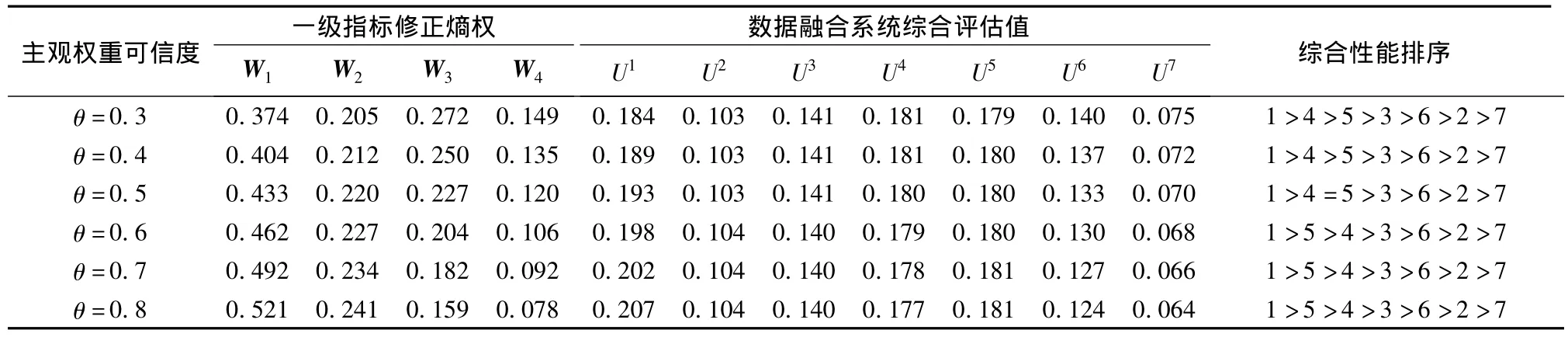
表2 数据融合系统综合评估数据Table 2 Comprehensive evaluation result of data fusion system
从表2来看,系统1显然综合性能最优,系统4和系统5的综合性能比较接近,其他系统次之,本文评估结果与单纯应用熵权法评估(结果为:4>5>1>3>6>2>7)相比有明显改进。与其他综合评估模型相比,如灰色关联分析法[5](评估结果为:1>5>4>3>2>6>7)、模糊层次分析法[8-9](评估结果为:1>5>3>4>2>6>7),本文针对不同层次指标的自身特点,综合考虑了指标数据自身不同角度的蕴含信息和物理意义,因而评估结果更具可信性,与专家分析判断也相一致。
4 结论
本文提出的基于粗糙集理论和修正熵权的评估模型对数据融合系统性能评估具有较强的针对性,利用粗糙集理论对指标数据进行属性约减,消除了冗余指标,降低了计算量;利用粗糙集计算属性权重对二级指标熵权进行修正,综合考虑了属性对决策分类的重要性和属性的信息量,提高了指标权值的客观性;利用层次分析法计算主观权重对一级指标熵权进行修正,考虑了影响数据融合系统性能各主要因素的物理意义,使评估结果更加可信。应用实例表明,该模型评估结果符合实际,客观性和操作性强,对数据融合系统的研制、论证和改进具有一定的应用价值。另外,本文提出的多层次多模型综合评估的思想,具备较强的扩展性和适应性,对其他应用领域的系统效能评估也具有一定的参考价值。
[1]何友,王国宏,陆大纟金,等.多传感器信息融合及应用[M].北京:电子工业出版社,2000.
[2]王骏,刘以安.分布式信息融合系统的性能评估方法[J].计算机工程与设计,2007,8(15):3773-3775.
[3]田杰,陈杰,窦丽华,等.多传感器信息融合性能的测试与评估[J].计算机工程,2003,29(10):84-85.
[4]陈自卫,陈华东.复杂电磁环境下的电磁频谱管理效能评估研究[J].指挥控制与仿真,2009,31(4):56-58.
[5]李阳,王朝英.粗糙集在数据融合系统性能评估中的应用[J].微电子学与计算机,2010,2(1):54-58.
[6]周晓,赵海燕,廖小健,等.基于多层次熵权的自行高炮机动能力综合评估[J].微计算机信息,2009,11(3):49-103.
[7]李阳.分布式数据融合评估关键技术研究及平台开发[D].西安:空军工程大学,2009.
[8]王健,肖文杰,王树文,等.用熵权模糊层次分析法的球载雷达模拟训练系统效能评估[J].电光与控制,2009,16(9):71-74.
[9]曹士信,张若庚,金鑫.基于组合熵权的联合作战目标选择模型研究[J].指挥控制与仿真,2008,30(6):16-19.

