交叉定位模糊区的精确几何分析

王洪迅， 弥小溪， 皇甫惠栋， 王 星， 王 超

(1.空军工程大学工程学院，西安 710038;2.中国人民解放军93802部队，陕西临潼 712200;3.中国人民解放军63655部队，乌鲁木齐 830000)

0 引言

无源定位以其独特的隐蔽优势广泛应用于战场预警、目标跟踪。双站测向交叉定位作为最重要的一种形式，受到国内外学者的重视和研究，理论和工程上已经取得了诸多进展。但是许多学者的研究重点是解决虚假定位以及优化布站问题，而对定位模糊区的研究相对较少，已有的研究大多采取概率统计或几何近似的方式，所得出的结论存在局限性，本文基于精确几何法进行研究，给出了模糊区的完整数学表达，通过仿真实验对模糊区与目标方位的关系进行分析，并与近似法进行对比得出了相关结论，对于纯方向无源定位策略的优化，提高定位精度具有一定重要参考意义。

1 交叉定位原理

双站交叉定位原理如图1所示。其中两个测向站O1(－R/2，0)和 O2(R/2，0)的位置已知，O3(x，y)为一个需要定位的目标辐射源。测向点O1和O2分别对目标O3辐射源实施测向可得到两条测向线，设两条测向线与 x轴的角分别为 θ1、θ2(其中 θ2'为 θ2的补角)，两测向线的交点就被认为是目标所在位置。

根据三角关系可知O3的坐标为

考虑由于测向不准所引入的定位误差，设两测向站测向误差分别为 ±Δθ1、±Δθ2，则定位出现模糊区ABCD(图1所示阴影区)，该区域面积即称之为定位模糊区面积，显然模糊区面积越小定位就越精确。

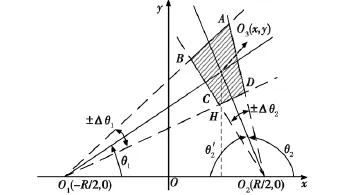
图1 交叉定位模糊区示意图Fig.1 The ambiguous-area sketch map of beam-crossing location

概率统计方式的主要思路是:将测向站的测向误差看作均值为零的高斯随机变量，于是交叉定位点的误差服从二元正态分布，而二元正态分布的等概率轮廓线为一个椭圆，其概率密度函数为

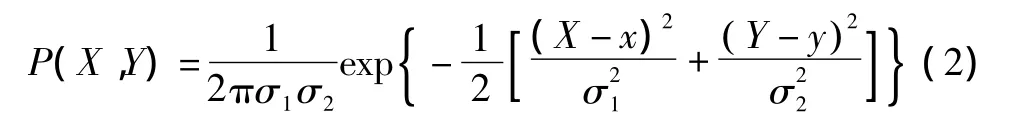
基于概率统计的方式，文献［1］分析交叉定位误差，研究了载机的最佳机动方向，文献［2－3］在不同的背景下研究了新的交叉定位算法。

文献［4］研究了交叉定位模糊区与交会角的关系，将两测向站的误差Δθ1，Δθ2看作小量从而得出模糊区的一种近似形式

式中，β=θ2－θ1。

文献［5－10］认为O3通常较远，该区域可近似为一个平行四边形，通过近似几何分析求得该区域面积如式(4)或式(5)所示。其中:H为O3到测量基线x轴的距离;R为两测向基站之间的距离;Δθ1、Δθ2单位为弧度。

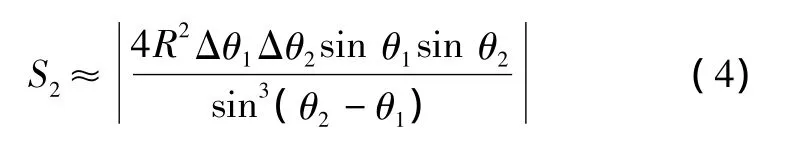
依据上式可得出以下结论:辐射源距离R越远，测向误差越大，模糊区面积也就越大;被测点与两个测向站连线之间距离H一定时，当θ1和θ2'均为π/3时模糊区面积最小［5－10］。至于几何近似对测向交叉定位误差分析的影响程度有多大文献中并未说明。

2 误差的精确几何分析

观察可知，两种几何近似实质上是相同的，近似的程度无从得知，分析图1的几何关系，四边形ABCD的面积是影响定位精度的重要因素，只有对其进行精确求解才能确定其变化规律，当目标与两测向站基线的夹角为0°时，误差趋于无穷大［11］，所以首先假定目标不在两测向站的基线或延长线上，即目标的位置坐标O3(x，y)中y≠0。于是可得出四边形ABCD的表达形式为

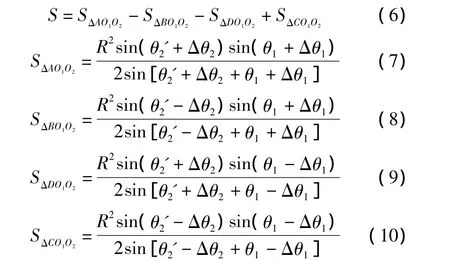
将式(7)～式(10)代入式(6)，此处略去详细推导过程，整理可得

或者

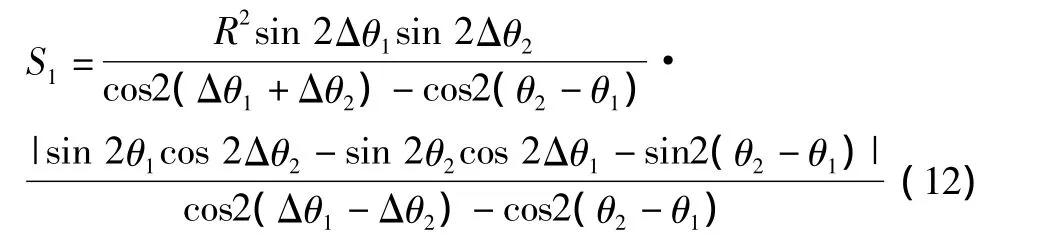
以上就是模糊区的精确数学表达。可以验证，当θ1，θ2(或)中任何一个为 π/2时，或者任一个为锐角，另一个为钝角时上述公式均成立。

3 仿真及分析

3.1 仿真条件

目标在空间所处的位置变化时，两个测向站对应于该目标的方位角随之改变，测得的模糊区也有所不同，为了得出模糊区面积的分布规律，仿真以平面上的目标位置为自变参数，模糊区面积为因变参数，x的范围为(－100 km，100 km)，y的范围为(0 km，200 km)，两测向基站坐标分别为(－50 km，0 km)、(50 km，0 km)。

3.2 结论分析

分4种情况进行仿真:1)Δθ1=Δθ2=π/90;2)Δθ1=Δθ2=π/120;3)Δθ1=Δθ2=π/180;4)Δθ1=π/90，Δθ2= π/180。

不同情况下的模糊区面积随目标方位的等值线分布如图2～图5所示。图中，横纵坐标代表方位(单位:km)，等值线上的数值代表模糊区面积(单位:km2)。

图2 模糊区面积分布(Δθ1=Δθ2=π/90)Fig.2 The ambiguous-area distribution(Δθ1=Δθ2=π/90)

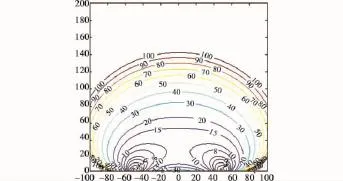
图3 模糊区面积分布(Δθ1=Δθ2=π/120)Fig.3 The ambiguous-area distribution(Δθ1=Δθ2=π/120)

图4 模糊区面积分布(Δθ1=Δθ2=π/180)Fig.4 The ambiguous-area distribution(Δθ1=Δθ2=π/180)

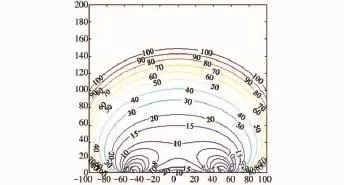
图5 模糊区面积分布(Δθ1=π/90，Δθ2=π/180)Fig.5 The ambiguous-area distribution(Δθ1= π/90，Δθ2=π/180)

由图2～图5可以分析得出以下结论。

1)模糊区面积随目标方位的分布中存在一个“驻点”，经计算，该驻点即 θ1=π/6，θ2=5π/6 时的测向交叉点，与测向误差无关，而且，在双站基线的中垂线意义上可以看作极小点，而在目标与双站连线意义上又是极大点。

2)定位模糊区的面积随着测角误差的增大呈上升趋势;模糊区的面积并不简单地随着目标距离的增加而增加，必须限定空域。

3)模糊区面积的最小值出现在两个测向站附近。

为了与近似法进行比较，在相同的条件下对近似法的结论做了仿真，近似法的模糊区面积用S2表示，两者的相对误差表示为

相对误差的等值分布如图6～图9所示。

图6 Δθ1=Δθ2=π/90相对误差分布Fig.6 The relative error distribution(Δθ1=Δθ2=π/90)

由图6～图9可以看出:1)随着双站测角误差的增大，近似法的模糊区相对误差增大，而且测角误差的不同对模糊区相对误差的分布有较大的影响;2)双站周围存在一个类月牙形区域，此区域之内对模糊区进行近似几何分析的结果与实际相当接近，可以代替精确结果，但此区域之外，近似法的误差较大，尤其当测角误差较大时，近似法的可信度不高，而精确几何法的结果比较合适。

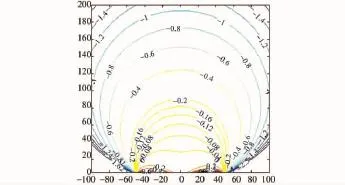
图7 Δθ1=Δθ2=π/120相对误差分布Fig.7 The relative error distribution(Δθ1= Δθ2= π/120)

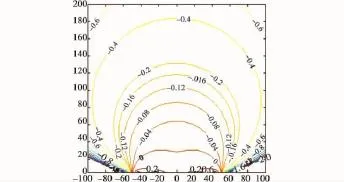
图8 Δθ1=Δθ2=π/180相对误差分布Fig.8 The relative error distribution(Δθ1= Δθ2= π/180)

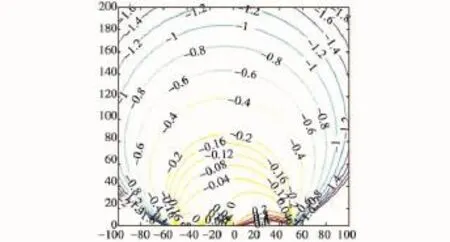
图9 Δθ1=π/90，Δθ2=π/180相对误差分布Fig.9 The relative error distribution(Δθ1= π/90，Δθ2=π/180)

4 结束语

本文研究了双站交叉定位的定位模糊区问题，给出了模糊区面积的完整数学表达，通过仿真确定了模糊区随目标位置的分布规律，并与近似法的分析结果做了对比，得出了相关结论，为双站以及多站无源定位传感器配置提供理论参考，具有一定借鉴意义。如何结合模糊区的精确分析结论尽可能提高无源定位的精度，使其在探测预警、引导武器发射方面发挥更大的作用，有待进一步研究。

［1］梁捷，谢晓方，曹建，等.机载多点测向交叉定位的最优机动方向研究［J］.电光与控制，2010，17(10):14-16，27.

［2］修建娟，何友，王宏国，等.纯方位系统中的定位模糊区分析［J］.系统工程与电子技术，2005，27(8):1391-1393.

［3］廖海军.一种新的测向交叉定位算法［J］.电光与控制，2008，15(9):29-31.

［4］王智显，徐汉林，熬庆.超远距离目标的交叉定位算法研究［J］.现代雷达，2008，30(12):39-42.

［5］赵国庆.雷达对抗原理［M］.西安:西安电子科技大学出版社，2003.

［6］刁鸣.雷达对抗技术［M］.哈尔滨:哈尔滨工业大学出版社，2007.

［7］张永顺，童宁宁，赵国庆.雷达电子战原理［M］.北京:国防工业出版社，2006.

［8］王红星，曹建平.通信侦察与干扰技术［M］.北京:国防工业出版社，2005.

［9］胡来招.无源定位［M］.北京:国防工业出版社，2004.

［10］王星.航空电子对抗原理［M］.北京:国防工业出版社，2008.

［11］王凯，张永顺，曹蕾，等.一种反干扰交叉定位算法研究［J］.电光与控制，2008，15(2):16-18.