无人机编队的滚动时域控制
华思亮, 尤 优, 张 红, 宋 晗
(1.中航航空电子有限公司,北京 100086;2.北京航空航天大学,北京 100191)
0 引言
和单架无人机相比,无人机编队在任务能力、灵活性、容错性等方面具有明显优势,在区域搜索、环境监测、协同作战等民用和军事领域得到了广泛应用[1-2]。
按照队形描述,无人机编队可分为固定编队和群集编队,固定编队中无人机之间的相对位置不变,形成固定队形;群集编队没有固定队形,每架无人机只与邻机保持适当距离。根据是否存在气动耦合,固定编队进一步分为紧密编队和松散编队。紧密编队控制对传感器精度的要求非常苛刻以致难以满足,因此在实际飞行中常结合不单纯依靠理论模型的极值搜索方法,通过实时测量燃料流和性能函数梯度的变化控制僚机位于最优气动位置[3]。松散编队控制在理论研究和实际飞行中都取得了较多进展,常见的松散编队控制方法包括PID控制、非线性控制、智能控制、滚动时域控制[4]等。位置关系描述是实现编队控制的前提,包括长机-僚机、广义坐标[5]、虚拟结构等。位置关系描述与控制方法的组合形成了不同的编队控制研究重点,本文研究应用范围较广的基于长机-僚机描述的松散编队控制。
滚动时域控制(Receding Horizon Control,RHC)是求解受约束优化问题的有效方法[4],在编队控制问题中应用RHC方法具有许多优点,如代价函数可以综合多种控制目标,滚动时域策略能够适应条件变化,具有处理控制输入约束和系统状态约束能力等。
本文采用二次规划模型对编队控制问题进行描述,并基于此分别设计了标准RHC和双模RHC编队控制器,分析了设计中的关键问题,最后进行了仿真实验和对比分析。
1 基于RHC的编队控制问题描述
1.1RHC 原理
RHC将控制问题描述为有限时域上有约束的最优化问题,具有在线处理控制约束和输出约束的优点。对于某个采样时刻,在系统状态约束和控制输入约束下对代价函数进行最优求解,得到预测时域内的最优控制输入序列;仅将其中第一项作用于系统,并将其余各项丢弃;系统状态在该控制输入的作用下变化;在采样时刻,根据新的系统状态重复以上过程,可得到该时刻的控制输入;如此反复进行即实现了系统的滚动时域控制。RHC的一般结构如图1所示。
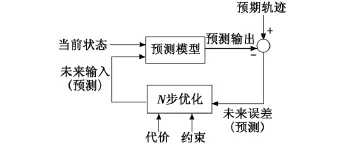
图1 RHC的一般结构Fig.1 General architecture of RHC
RHC中可采用数学规划方法对编队控制问题进行建模。数学规划模型的选取决定了问题描述精确度和在线求解的实时性,这二者往往是矛盾的,需要根据需求进行权衡。非线性规划具有最好的问题描述能力,但求解困难且实时性难以保证。二次规划具有较好的问题描述能力,且当代价函数的二次项参数矩阵是正半定阵时,二次规划是凸优化问题,具有很好的求解可行性和快速性。下面基于二次规划模型在有限时域上对编队控制问题进行描述。
1.2 无人机预测模型
在基于RHC的编队控制研究和飞行试验中,为了保证在线求解的实时性,常采用反馈线性化后的无人机模型或质点模型,如 Honeywell公司 Organic Air Vehicle飞行器[4]以及 Boeing 公司 F-15A、T-33[6]的编队控制。本文采用文献[4]中的线性模型对无人机进行建模。
假设各无人机飞行高度相同,无人机控制输入有最大限幅,同时无人机受最大飞行速度约束。无人机模型为

迭代上式可得到系统状态的预测值为

式中,xk+i|k表示在k时刻对无人机k+i时刻状态的预测,显然当i=0时,xk|k=xk。为了描述方便,将无人机在k时刻对k+1,…,k+N时刻的状态预测和相应控制输入写成向量形式:=(xk+1|k,xk+2|k,…,xk+N|k)T,=(uk|k,uk+1|k,…,uk+N-1|k)T从而得到仅由当前状态xk和控制输入序列表达的形式

其中:Hx=(A,A2,…,AN)T;
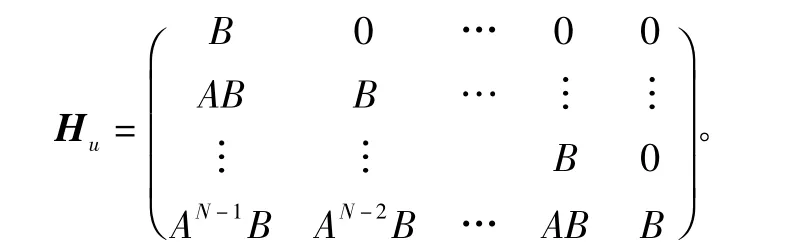
1.3 代价函数设计
编队控制的控制目标是无人机间保持固定位置关系,同时所需的控制输入较小,因此代价函数中应包含系统状态代价项和控制输入代价项。RHC需要在当前时刻后的固定时域内进行优化解算,需在该时域内设计代价函数。选取2范数作为代价函数的基本项,设固定时域长度为N,则僚机RHC控制器的代价函数为

式中:xref,k+i+1为预期系统状态;uref,k+i为预期控制输入;uk+i|k表示在k时刻对无人机k+i时刻控制输入的预测。加权阵P,Q为正定矩阵,即 P=PT>0,Q=QT>0。为了得到较小的控制输入,取预期控制输入为零。将式(3)代入式(4),可得
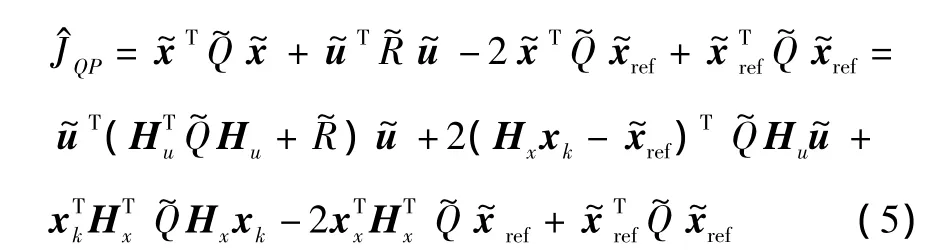

由上式可见,代价函数JQP是系统初始状态xk和控制输入序列的函数,其中是决策变量。对于每个确定的系统初始状态xk,通过求解有约束的二次规划问题可以得到一组最优的控制输入序列。
1.4 约束条件设计
编队控制问题的约束条件是无人机的最大速度和最大控制输入限幅,即

式中:Cx∈Rnv×n;nv为需要约束的分量数,Cx的元素仅包含0和1,Cx使转化为中速度分量组合成的向量。
二次规划只能处理仅包含决策变量的约束,因此式(7)需转化为决策变量表达的形式。将式(3)代入式(7),得到

从而得到状态约束的决策变量表达。
1.5 编队控制问题描述
由式(6)~式(9),编队控制的有限时域二次规划模型为
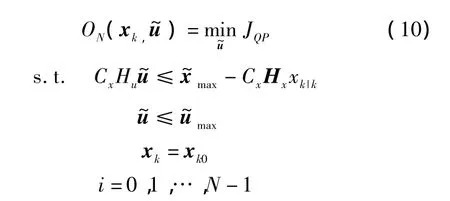
优化问题(10)中,ON(xk,)表示优化问题 ON是xk,的函数,是时刻 k+i(i=0,1,…,N -1)时无人机控制输入组成的序列,也是优化问题的决策变量。xk是系统初始状态,其值为xk0。对于某个确定的系统初始状态xk0,通过求解优化问题(10),可以得到性能指标的最小值,以及对应的最优决策变量,即有限时域内系统的最优控制输入序列。
1.6 RHC编队控制器
RHC编队控制器的基本过程是:
1)在采样时刻k,僚机状态为x0,求解优化问题(10),得到未来N步的最优控制输入序列;
2)将最优控制输入序列的第1项作用于僚机,其余N-1项舍弃;
3)在控制输入作用下,僚机在采样时刻k+1到达新状态x1;
4)将当前时刻记为k,僚机状态记为x0,返回步骤1)。
2 双模RHC编队控制器
2.1 设计思路
RHC中优化问题存在可行解并不能保证闭环系统稳定,例如预测时域过短时可能出现振荡或发散的情况。双模RHC是一种保证稳定性的方案[7],其基本思路是引入终端不变集 Ωf和对应的控制器 uk=h(xk),当系统状态在Ωf外时采用标准RHC算法,并限制预测状态在时域终端进入Ωf;当实际状态进入Ωf时切换到控制器uk=h(xk),由局部控制器保证Ωf内系统稳定。Limon证明双模RHC可以用一个预测时域更长的标准RHC等价[8]。
以上方案应用于编队控制问题存在一些不足。1)预测失配问题。长机实际状态和僚机对其预测状态间的偏差随着预测时域增加而增大,文献[4]给出了预测时域过长时编队不稳定的证明。2)双模RHC设计方案保守,可行解的存在需要较长的预测时域保证,此时采用标准RHC往往也闭环稳定。
尽管存在以上问题,但双模RHC编队控制器对标准RHC的改进和参数选取具有指导意义,如预测时域选取、终端加权设计等。
考虑长机定常飞行时僚机双模RHC控制器的设计。首先确定局部控制器和终端代价函数,然后求解此控制器对应的不变集和终端代价。双模控制器具有不同的设计方法,具体体现在局部控制器、终端不变集和终端代价函数的选择以及不同的计算方法。本文以最优控制器作为局部控制器,选取椭球描述的终端不变集以及二次加权形式的终端代价函数构造控制器。
2.2 局部控制器与终端不变集设计
局部控制器为

选取椭球集作为终端不变集
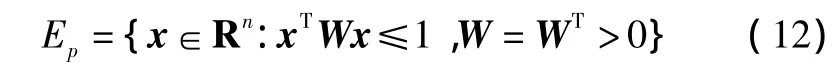
若存在一个矩阵W=WT∈Rn×n满足矩阵不等式
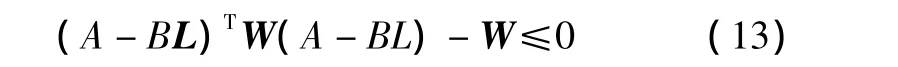
则椭球Ep={x∈Rn:xTWx≤1}是系统(11)关于控制器(12)的不变集[9],即满足不等式Wxk+1≤Wxk。
针对确定的局部控制器,若存在一个不变集,则该不变集的子集显然也是该局部控制器的不变集,因此不变集的确定对控制器设计的保守性有较大影响。受约束线性时不变系统的最大不变集是一个多面体集,该集合计算和表示比较复杂[10]。
通过求解 MAXDET 问题(14)[11],可得到椭球不变集xTWx≤1,该不变集是对最大不变集的一种近似。
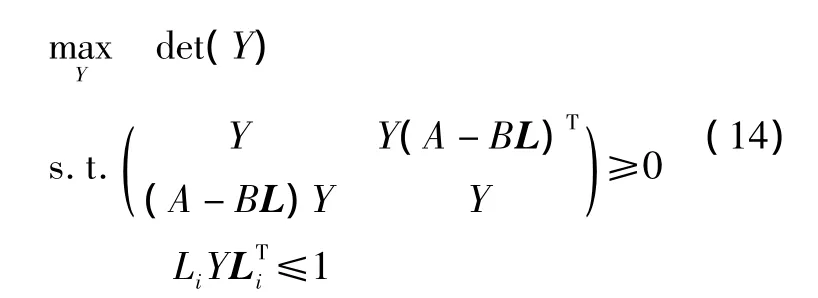
其中:Y=W-1;Li是L的第i行。
2.3 终端加权设计
选择终端加权为二次代价形式

其中:P=PT>0,且满足线性矩阵不等式[11]

式中:Q和R是前N-1项状态和输入的加权,选取合适的Q和R,由上式可得到终端加权P。
3 仿真分析
以Honeywell公司的 Organic Air Vehicle(OAV)飞行器编队为仿真研究对象,基于内环反馈线性化后的线性OAV模型,在外环进行编队控制。OAV的动力学特性及坐标系建立详见文献[4]。OAV数学模型为[4]

式中:xk=(xk,x,xk,y,xk,vx,xk,vy)T的分量为无人机 x 和 y方向的位置和速度;uk=(uk,x,uk,y)T的分量为 x 和 y方向的控制输入;B=diag(Ts,Ts),Ts为采样时间。只给出x方向的仿真结果和分析,y方向的情况与之类似。约束优化问题求解采用Matlab优化工具箱,MAXDET问题求解采用Sedumi软件。
3.1 双模RHC编队控制
最优控制器的状态和输入加权选取为单位阵,局部控制器为u= -(0.8410 1.6321)x,局部控制器对应的椭球不变集为
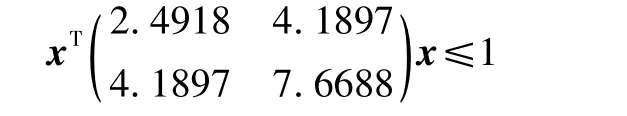
令状态加权Q=diag(1,1),控制加权R=1,终端代价函数为

双模RHC可以很好地控制僚机收敛于预期轨迹,同时有效地约束系统状态和控制输入。将预测时域减小到9时,尽管仍能得到优化问题的可行解,但终端预测状态未进入不变集,不满足双模RHC的条件;预测时域等于或大于10时,终端状态可以进入不变集。然而在预测时域为9时,采用标准RHC控制器仍可得到与图2同样的控制效果,这体现了双模RHC控制器设计的保守性。
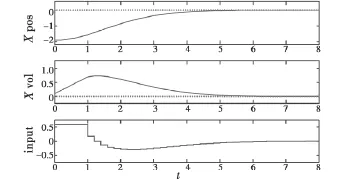
图2 基于双模RHC的编队控制(N=10)Fig.2 Formation control based on dualmode RHC(N=10)
优化问题求解所需时间平均为0.032 s,由于Matlab是解释性语言,若使用编译后的优化求解代码,快速性还将进一步提高。
3.2 标准RHC编队控制:预测时域的影响
RHC中决策变量数与预测时域长度成正比,较小的预测时域会降低优化求解的复杂度,提高求解速度,然而预测时域过小会使控制器性能变差,甚至引起闭环系统不稳定。将长机运动扩展到机动飞行的情况。参数选取情况为:=2,=0.6,xk0=(0,0)T,Q=diag(1,0.2),R=0.5,N=5,Ts=0.2。僚机 x 方向的动态响应如图3所示。

图3 基于标准RHC的编队控制(N=5)Fig.3 Formation control based on standard RHC(N=5)
标准RHC控制器有效地限制了系统控制输入,控制在达到限幅时受到约束,但僚机位置始终在预期位置附近震荡,无法跟踪长机。由于预测步长较小,优化问题仅考虑较短时域内的情况,闭环系统不稳定。将预测时域增加到10,其他参数不变,僚机x方向的动态响应如图4所示。僚机的位置和速度均很好地跟踪了长机。由于状态预测的作用,控制量会提前反应以适应控制目标的未来变化。
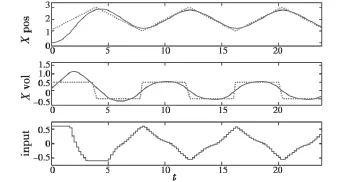
图4 基于标准RHC的编队控制(N=10)Fig.4 Formation control based on standard RHC (N=10)
3.3 标准RHC编队控制:终端加权的影响
终端代价函数的作用是使代价函数逼近无限时域时的情况,因此较大的终端加权可以改善系统的稳定性。在第3.2节中预测时域N=5时闭环系统不稳定,将终端权值 Qt=diag(1,0.2)增大为 Qt=diag(60,12),其他参数不变,可得到稳定的闭环系统,如图5所示。

图5 基于标准RHC的编队控制(终端加权影响)Fig.5 Formation control based on standard RHC(with terminal penalty)
僚机在预期位置附近短暂震荡后收敛到预期位置,并且能够跟踪长机机动,但轨迹收敛的时间长于第3.2节中N=10的情况。
4 结束语
本文基于二次规划模型设计了编队控制的RHC控制器,该控制器具有良好的控制效果、约束处理能力和快速性。针对滚动时域控制稳定性问题,结合不变集理论设计了双模RHC控制器,该控制器对标准RHC控制器的预测时域、终端加权等参数设计具有指导意义。通过仿真实验验证了RHC编队控制器设计的有效性,并对比分析了不同参数选取对闭环系统性能的影响。下一步将重点在RHC编队控制器的动态环境适应性方面开展研究。
[1]WANG X H,YADAV V,BALAKRISHNAN S N.Cooperative UAV formation flying with obstacle/collision avoidance[J].IEEE Transactions on Control System Technology,2007,15(4):672-679.
[2]刘小雄,章卫国,李广文,等.无人机自主编队飞行控制的技术问题[J].电光与控制,2006,13(6):28-31.
[3]LAVRETSKY E,HOVAKIMYAN N,CALISE A,et al.Adaptive vortex seeking formation flight neuro control[C]//AIAA Guidance Navigation and Control Conference and Exhibit,2003:5726.
[4]KEVICZKY T,BORRELLI F,BALAS G J.Decentralized receding horizon control for large scale dynamically decoupled systems[J].Automatica,2006,42:2105-2115.
[5]SPRY S,HEDRICK K.Formation control using generalized coordinates[C]//The 43rd IEEE Conference on Decision and Control.Atlantis.2004:2441-2446.
[6]SCHOUWENAARS T,VALENTI M,FERON E,et al.Implementation and flight test results of MILP-based UAV guidance[C]//IEEE Aerospace Conference.2005:1-13.
[7]MAYNE D Q,RAWLINGS J B,RAO C V,et al.Constrained model predictive control:Stability and optimality[J].Automatica,2000,36:789-814.
[8]LIMON A,ALAMO T,SALAS F,et al.On the stability of constrained MPC without terminal constraint[J].IEEE Transactions on Automatic Control,2006,51(5):832-836.
[9]KERRIGAN E C.Robust constraint satisfaction:Invariant sets and predictive control[D].Cambridge:University of Cambridge,U.K,2000.
[10]GILBERT E G,TAN K T.Linear systems with state and control constraints:The theory and application of maximal output admissible sets[J].IEEE Transactions on Automatic Control,1991,36:1008-1020.
[11]LOFBERG J.Linear model predictive control stability and robustness[M].Sweden:Linkopings University,2001.

