一种高带宽四舵翼电动舵机的可行性研究

崔业兵， 鞠玉涛， 周长省， 郑健

(南京理工大学机械工程学院，江苏南京210094)

0 引言

简易制导弹药具有成本低、命中精确度高、工程实现简单等特点，引起各国军方重点关注。国外普遍采用脉冲推力器和舵机作为简易控制的主要执行机构［1－2］，然而脉冲发动机存在修正力大小有限，安装位置要求苛刻以及喷流对原弹的气动特性也有很大的影响等问题，采用舵机进行弹道修正，能很好地解决或避免这些问题［3］。电动舵机与液压舵机、气动舵机相比，具有结构紧凑、易于维护、经济性好等优点，成为未来常规弹药制导化发展的一项关键技术［4］，其作用是驱动空气舵翼或燃气舵片等作为简易制导弹药的执行机构，并配合其他部件实现弹药的可控飞行，达到常规弹药精确打击的目的［5］。

目前国外已经在航天器和制导弹药中应用了电动舵机，无人机、战术导弹响尾蛇AIM－9X和X43高超音速飞行器的带宽最小为7.5 Hz;国内的无人机用电动舵机带宽在2 Hz左右，因为无人机的飞行速度一般为200 m/s左右，其固有频率较低，易于控制。但是对于飞行速度为1 200 m/s的常规弹药采用如此低带宽的电动舵机，无法实现有效飞行姿态控制。国内对电动舵机的研制虽然已经取得了一定进展，但与实际应用还有较大的差距［6］。

针对常规弹药弹道末修正技术对电动舵机的性能要求，以高带宽大于10 Hz为设计目标，对四舵翼的电动舵机设计方案和其中的关键技术进行研究，通过仿真和样机的加载实验，对所设计的电动舵机的性能进行验证，主要研究舵机系统在位置指令跟踪和力矩干扰抑制双重控制目标下的控制性能。

1 高带宽四舵翼电动舵机的方案分析

本文设计的舵机针对常规弹药弹道末修正的技术要求，必须满足以下基本要求:舵偏角为±20°;系统带宽大于10 Hz。位置指令跟踪的动态性能指标要求为:输出转角单位阶跃响应的上升时间tr≤0.1 s;稳态误差ess≤1%;超调量σ≤10%。力矩干扰抑制的动态性能指标要求为:输出转角单位阶跃响应的峰值 ymax≤0.4°;稳态值 yss≤0.1°。功率限制指标要求为单位阶跃响应时控制器输出电压峰值Umax≤20 V，其中功率限制指标是针对伺服机构动力电池的性能提出的，同时要求舵机能够实现俯仰、偏航、滚转控制功能。文献［2］中提出的由1个电机带动4个舵轴的方案虽然巧妙，但是其间的机械结构不但复杂庞大，且舵机的联动控制实现困难;文献［6］中设计了直线式的作动器，通过多个作动器的联动能够实现航天器俯仰、偏航2个方向的摆动，但是安装空间较大，且不能实现滚转控制。本文设计的舵机采用4通道结构方案，如图1所示。其中电机、传动机构、舵翼展开锁紧机构等部件为独立4套机构，分别驱动4个舵翼。本方案电动舵机的关键技术涉及传动机构设计、舵翼展开锁紧机构设计、舵轴位置的确定、驱动控制技术等。

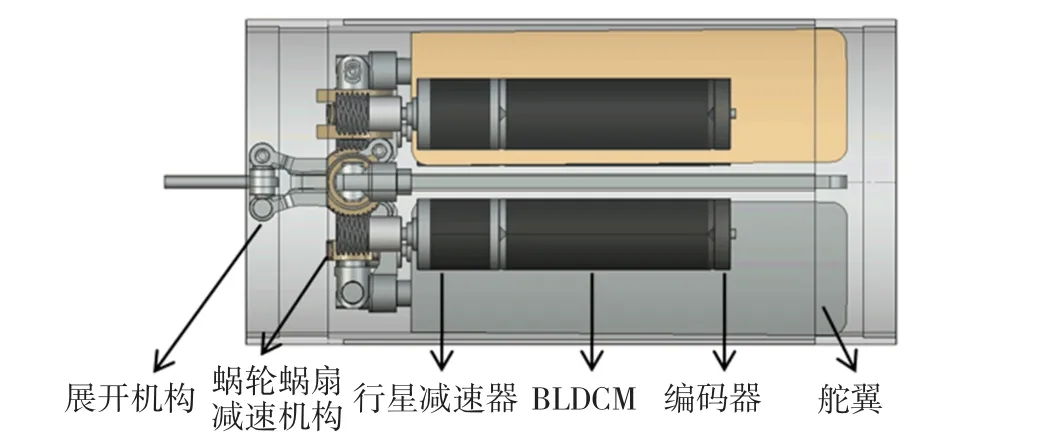
图1 四舵翼电动舵机结构Fig.1 Basic structure of the four rudder wings EMA

1.1 舵机系统的传动机构设计

根据电动舵机高可靠性、高功率质量比和环境温度苛刻的要求，驱动电机选择能够耐受高低温的钐钴永磁体的永磁式无刷直流电机(brushless direct current motor，BLDCM)，额定转速为 16 800 r/min。而传动机构设计主要从系统的带宽、结构布局、传动效率和精确度要求等方面来考虑［7－8］，初步确定当系统带宽大于等于10 Hz时，舵机的减速比为118.8。采用两级传动方式:第一级用与电机串联的行星齿轮减速箱，传动比i12=5.4;第二级用蜗轮蜗杆传动，改变传动方向，减速比i23=22。目前，作动器机械传动部分存在的主要问题是减速器间隙引起的非线性及振荡问题和空间环境中的润滑问题。减速器间隙在舵机频繁正反向调节时引起的系统振荡必须要消除［9－10］。本文设计的舵机拟从两方面解决该问题:1)采用高精确度的传动件，控制输出轴的控制精确度。本传动机构中的齿轮箱空回约为1°，折算到输出轴约为(1/118.8)°，可忽略;由于体积限制，所有转动轴均未加滚动轴承，均为滑动，考虑到材料的膨胀系数的不同，为保证在－20℃ ～50℃内均可灵活转动，在各轴和孔之间须额外保留一定的间隙，此间隙大约为0.01 mm;另外还有蜗轮蜗杆加工和安装误差，初步估计输出轴控制精确度大约在0.5°左右。2)通过控制方法消除减速器的振荡;其次润滑是保证舵机可靠性和正常运行的重要途径，用来保证运动副不出现冷焊现象，并具有良好、稳定的摩擦特性。由于液体润滑剂在空间环境中容易流失，因此采用固体润滑。

1.2 舵翼展开锁紧机构的设计

由于体积限制，无法将传动机构以及电机等随舵翼的展开而转动，所以本方案仅将舵翼转动，而电机和减速机不随舵翼的展开而转动，采用弹簧加连杆的设计方法来展开舵翼，具体设计如图2所示(左边为展开前的状态，右边为展开后的状态，图中未画压簧，中间直杆为导向作用)。展开后的自锁采用压簧加锁销的方法来实现。

图2 舵翼展开锁紧机构Fig.2 Unlocking and locking mechanism of the rudder wings

1.3 舵机系统舵轴位置的确定

因为舵面在空中运动时要承受较大的空气动力载荷，通常称之为铰链力矩。铰链力矩作为舵机的主要负载转矩，其大范围变化，必将影响舵机的工作性能，甚至破坏其运动规律［11］。因此舵机的输出轴位置应尽量在舵翼的气动压心位置，在此位置舵翼承受的铰链力矩最小，从而保证舵机的控制性能。本方案设计的舵翼尺寸为120 mm×47 mm×4 mm，舵轴的位置初步确定为距离舵翼前缘15 mm处(宽为47 mm)，并利用Fluent软件对舵翼的二维流场进行仿真分析，得到舵翼的气动特性，详见表1。

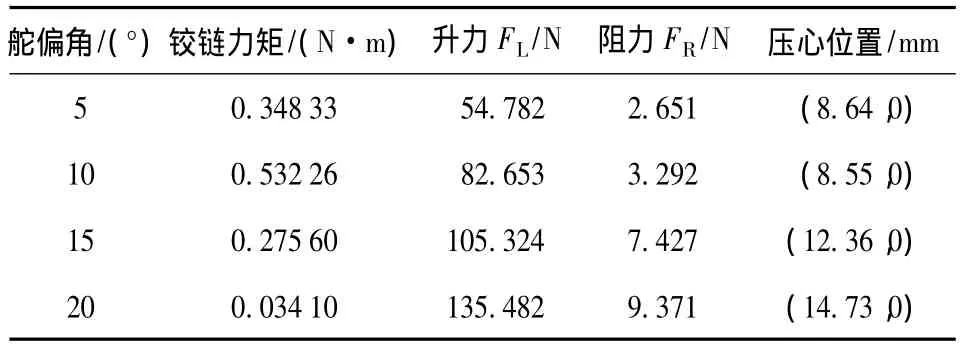
表1 气动特性数据表Table 1 Data of Aerodynamic characteristics

由仿真可知，在舵轴位置的铰链力矩很小，因此设计的舵轴位置是合理的，能够满足舵机的控制要求。

1.4 舵机系统的驱动控制技术

舵机控制系统主要由上位机PC、CAN总线通信模块、DSP电机控制器、功率放大电路和直流无刷电机以及反馈传感器等组成。其中由电机、电位计、传动机构、电机驱动电路和DSP控制器构成一套闭环的位置控制系统。上位机PC代替制导计算机功能，电动舵机正常工作时，DSP控制器接受上位机PC给定的舵面偏转指令，驱动伺服电机带动舵面偏转，同时DSP控制器通过旋转电位计实时采集实际的舵面角度，保证舵面在一定的响应时间内以一定的精确度趋近给定角度值，从而使简易控制弹药完成弹道的修正。

2 电动舵机模型的建立

2.1 电动舵机的建模

对设计的电动舵机是4通道的系统建立其数学模型时，只需要对单通道舵机进行建模，就能表征整个系统。为简化起见，忽略传动环节转换的非线性，将传动环节的质量特性分别折算到电机轴和负载轴上，从而可将被控对象视为由舵机和负载组成的二自由度系统，如图3所示。

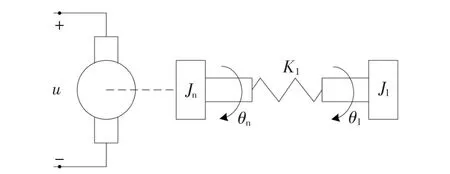
图3 舵机二自由度动力学模型Fig.3 Two-degree of freedom dynamics mode of EMA

根据图3可以得到单通道舵机的支配方程，舵机部分的电压方程为

式中:u为电枢电压;L为电枢总电感;R为电枢总电阻;i为电枢电流;Ke为反电动势系数;ωm为电机输出轴转速。运动方程为

式中:Kt为转矩系数;Jn为系统折算到电机轴的转动惯量;bn为系统折算到电机轴的粘性阻尼系数;θm为电机轴的输出转角;T1为负载端输入力矩;N为传动机构的减速比。

舵轴输出角ωn和电机反电动势E的表达式为

负载部分方程为

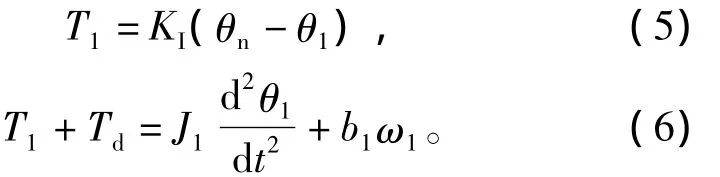
式中:b1为系统粘性阻尼系数;J1为系统折算到负载轴转动惯量;θn，θ1分别为舵机、负载输出转角;KI为舵机和负载之间耦合刚度系数;ω1为负载端输出角;Td为外部干扰力矩。

2.2 带前馈的模糊PID控制器设计

虽然建立了电动舵机的二自由度模型，但还是会存在一定的误差;舵翼上的铰链力矩随着飞行状态的变化，如飞行马赫数、舵面的偏转角度等，将在很大范围内变化，铰链力矩作为舵机的主要负载转矩，其大范围变化，必将影响舵机的工作性能，甚至破坏其运动规律。同时由于无刷直流电机的参数摄动与换相过程的非线性，这些因素将对舵机系统的控制性能产生严重的影响，普通的PID控制器满足不了舵机系统的控制要求［10］，因此设计如图4所示的带前馈的模糊PID控制器。

图4 舵机系统控制框图Fig.4 Block-diagram representation of EMA control system

舵机控制器采用串级控制，分为电流环(automatic current regulator，ACR)、速度环 (automatic speed regulator，ASR)和位置环(automatic position regulator，APR)。这样可以保证系统的稳定性和响应速度，当ASR和ACR内部的参数发生变化或者受到扰动时，他们能起到有效的抑制作用，减少APR的影响，从而可以保证系统的稳定。ACR需要具有快速跟踪性能，采用积分超前滞后校正，没有引入微分控制，主要考虑不引起ACR振荡，保证系统有足够的电流来加速负载惯量。APR作为3环的最后1环，由于舵机负载转矩产生的非线性主要作用于此环，因此该环的非线性较大，采用传统的PI控制难以满足控制要求，本文引入了模糊自整定参数的PID控制器［12－14］，将前馈控制和PID控制结合起来，经过前馈控制后，PID控制器仅需修正残余的误差，因此改善了整个系统的响应性能，可以使舵机系统在参数变化、存在未建模误差时具有更高的动静态性能和鲁棒性，从而减小了负载力矩扰动对舵机性能的影响［15－17］。

3 舵机系统的仿真与实验分析

为了检验设计的电动舵机系统是否能够达到性能指标的要求，进行舵机系统的仿真分析与原理样机实验。研究对象的模型参数为:L=66.4×10－3H;R=0.466 Ω;N=118.8;Ke=0.06 V·s/rad;Kt=0.019 2 N·m/A;Jn=1.83×10－5kg·m2;bn=8.5×10－5N·m/(rad/s);J1=3.5×10－4kg·m2;b1=1×10－3N·m/(rad/s);KI=1.49×103N·m/rad。

通过Matlab/SIMULINK工具建立了舵机系统的动态仿真模型，如图5所示，需要研究不同算法对电动舵机性能的影响，可以改变舵机系统模型中控制器的不同控制算法仿真模型。

图5 系统仿真整体结构Fig.5 The whole simulation structure of the system

当飞行器的飞行马赫数一定时，可以近似假设此时的铰链力矩为一弹性负载(铰链力矩大小与舵面偏角成正比)，据此设计了基于悬臂梁的舵机弹性加载测试系统，如图6所示。通过基于弹性悬臂梁的比例加载，对设计的电动舵机进行多次加载实验，验证了电动舵机在负载情况下，对阶跃输入信号、正弦输入信号、力矩干扰信号的响应特性，充分考查了设计的舵机系统的快速性、系统带宽、对位置指令的跟着性能以及对力矩干扰信号的抑制能力。

图6 电动舵机系统加载测试台Fig.6 Specification of the EMA loading and test bench

在单位阶跃信号输入下，检验舵机系统的快速性。图7为舵机系统的阶跃响应仿真曲线。

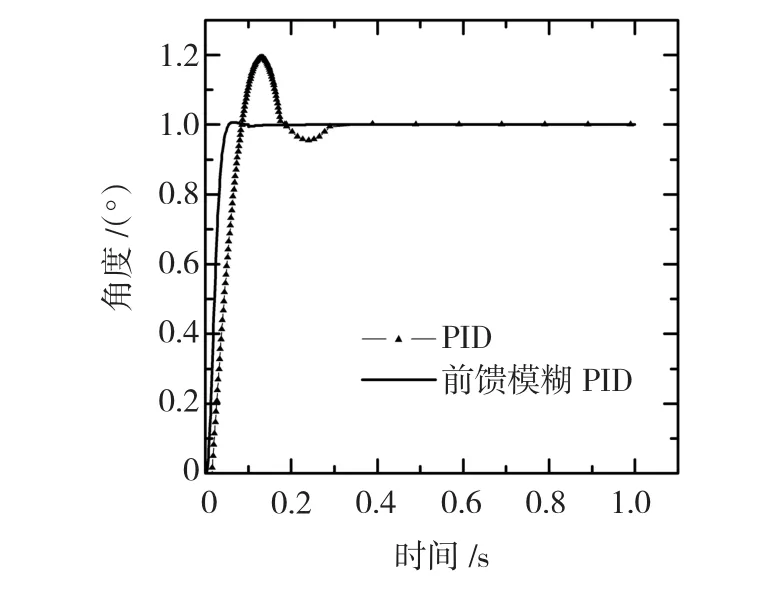
图7 电动舵机系统阶跃响应仿真曲线Fig.7 Simulation step response of the EMA with PID and feed-forward fuzzy self-tuning PID

图8为电舵机系统负载时5°阶跃响应实验曲线，从图中可以看出，实验获得的阶跃响应曲线与仿真曲线基本上是一致的，采用PID控制器的上升时间为25 ms，超调量为15%左右;采用前馈模糊PID控制器的上升时间为15 ms，且超调量很小。图9为舵机连续阶跃响应曲线。表2为舵偏角分别为 5°、10°、15°、20°阶跃响应时对应的上升时间、超调量、稳态误差、控制器输入电压峰值，由图7～图9和表2可知，电动舵机采用前馈模糊PID比普通PID上升时间更快，动态性能更好，超调更小。

图8 电动舵机系统5°阶跃响应加载实验曲线Fig.8 Experimental 5°step response of the EMA with PID and feed-forward fuzzy self-tuning PID

图9 电动舵机系统连续阶跃响应加载实验曲线Fig.9 Experimental multiple-step response of the EMA with PID and feed-forward fuzzy self-tuning PID

表2 系统的阶跃响应性能Table 2 Step response of the system performance

通常系统动态性能的测试通过输入位置指令为正弦信号(在不同的角度和不同的频率下)，判断出舵机系统对正弦位置指令的跟踪能力。从如图10所示的正弦响应仿真曲线和如图11所示的正弦加载实验曲线中可以看出，对于15°5 Hz的正弦指令的跟踪能力，前馈模糊PID优于普通PID控制器，并且通过一系列在不同频率和不同角度下的正弦加载实验，可以得到舵机系统偏转不同的角度对应的频率特性，从而可知系统在负载状况下的实际带宽范围，如图12所示(频率特性图是舵机采用前馈模糊控制器的实验数据绘制)。舵机系统的带宽在舵偏角为 5°、10°时达到 15 Hz左右，而在 15°、20°时只有10 Hz左右。通过弹性悬臂梁进行舵机的加载测试时，舵机系统的输出力矩与舵偏角成一定的比例。由图12可知，输出力矩随频率的增加而减小。

图10 电动舵机系统15°5 Hz正弦响应仿真曲线Fig.10 Simulation response due to 15°in 5 Hz sine input of the EMA with PID and feed-forward fuzzy self-tuning PID

图11 电动舵机系统15°5 Hz正弦响应加载曲线Fig.11 Experimental response due to 15°in 5 Hz sine input of the EMA with PID and feed-forward fuzzy self-tuning PID

图12 电动舵机系统对应不同角度的频率特性Fig.12 The EMA frequency response due to different angle

关于系统的力矩干扰实验，本文主要通过在阶跃响应进行过程中突然加载一个扰动力矩来实现的。多次数据采集处理结果表明，系统对干扰力矩的响应峰值 ymax=0.15°，稳态值 yss≤0.05°，满足系统指标要求。

4 结语

本文主要根据简易制导弹药对舵机的性能要求，从舵机系统的结构、硬件和软件设计等方面综合考虑如何提高系统的带宽。设计了基于CAN总线和DSP电机控制的四舵翼电动舵机系统，并充分考虑负载转矩变化对舵机系统性能的影响，设计了带前馈的模糊自整定的PID串级控制器，仿真和实验分析结果表明，设计的四舵翼电动舵机系统在最大舵偏角20°时，带宽达到10 Hz，具有高速、高精确度、较好的动态特性和鲁棒性等特点。同时该舵机系统通过CAN总线的指令传输可以实现四舵翼的差动、联动控制，从而能够进行实时的修正弹道以及弹体的滚转、俯仰和偏航的姿态调整，从而为未来常规弹药制导化发展提供一定的参考。

［1］ 史金光，王中原.简易控制修正力技术研究［J］.弹道学报，2006，18(1):14 －18.

SHI Jinguang，WANG Zhongyuan，et al.A study on correctional force for simple control［J］.Journal of Ballistics，2006，18(1):14－18.

［2］ 王俊全，王晓鸣，李文彬.新型四轴联动舵机的原理和动力学分析［J］.兵工学报，2006，27(1):54 －57.

WANG Junquan，WANG Xiaoming，LI Wenbin.The principle and dynamics analysis of a four-shaft-linked actuator［J］.ACTA ARMAMENTARII，2006，27(1):54 －57.

［3］ 宋锦武，祁载康.简易制导脉冲控制力修正技术研究［J］.北京理工大学学报，2004，24(5):383 －386.

SONG Jinwu，QI Zaikang.A study of the correction technique of impulse control force for simple guided projectiles［J］.Journal of Beijing Institute of Technology，2004，24(5):383 －386.

［4］ CHARRIER J J，KULSHRSHTHA A.Electric actuation for flight＆engine control system:Evolution，current trends＆ future challenges［C］//Collection of Technical Papers-45th AIAA Aerospace Sciences Meeting，January 8 －11，2007，Reno，USA.2007，23:16421－16440.

［5］ SCHINSTOCK D E，HASKEW T A.Dynamic load testing of roller screw EMAs［C］//Proceedings of the Intersociety Energy Conversion Engineering Conference.Auguest 11 － 16，1996，Washington，USA.1996:221－226.

［6］ 陆豪，李运华，朱成林.某型航天器推力矢量控制伺服机构的设计理论［J］.北京航空航天大学学报，2010，36(12):1417－1421.

LU Hao，LI Yunhua，ZHU Chenglin.Design theory of thrust vector control servo mechanism for a type of spacecraft［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36(12):1417－1421.

［7］ 郭宏，邢伟.机电作动系统发展［J］.航空学报，2007，28(3):620－627.

GUO Hong，XIN Wei.Development of electromechanical actuators［J］.ACTA AERONAUTICA ET ASTRONAUTICA SINICA，2007，28(3):620 －627.

［8］ 于志远，姚晓先，戴闰志，等.压电舵机微位移放大机构设计［J］.兵工学报，2009，30(12):1653 －1657.

YU Zhiyuan，YAO Xiaoxian，DAI Runzhi，et al.Design of micro displacement amplifier of piezoelectric servo［J］.ACTA ARMAMENTARII，2009，30(12):1653 －1657.

［9］ GUO Hong，WANG Wei，XING Wei.Design of electrical/mechanical hybrid 4-redundancy brushless DC torque motor［J］.Chinese Journal of Aeronautics，2010，23(2):211 －215.

［10］ LU Hao，LI Yunhua，TIAN Shengli，et al.Improved hybrid robust control method for the electromechanical actuator in aircrafts［J］.Chinese Journal of Mechanical Engineering，2010，23(4):443－450.

［11］ 景蓉，彭舒钰.小型电动比例舵机研究［J］.航空兵器，2002，37(3):18－20.

JING Rong，PENG Shuyu.Small electromechanical actuator research［J］.Aero Weaponry，2002，37(3):18 － 20.

［12］ YANG S F，CHOU J H.A mechatronic positioning system actuated using a micro DC-motor-driven propeller-thruster［J］.Mechatronics，2009，19(6):912 －926.

［13］ MENDES Jerome，RUI Araujo，SOUSA Pedro，et al.An architecture for adaptive fuzzy control in industrial environments［J］.Computers in Industry，2011，62(3):364 －373.

［14］ ARRIETA O，VISIOLI A，VILANOVA R.PID autotuning for weighted servo/regulation control operation ［J］.Journal of Process Control，2010，20(4):472 －480.

［15］ 年漪蓓，高国琴.一类不确定非线性系统的自适应模糊滑模控制［J］.电机与控制学报，2005，9(5):512 －514.

NIAN Yibei，GAO Guoqin.Adaptive fuzzy sliding mode control for a class of uncertain nonlinear system［J］.Electric Machines and Control，2005，9(5):512 －514.

［16］ 王占友，谢顺依.改进BLDC转矩性能的模糊控制器的设计［J］.电机与控制学报，2009，13(6):913 －918.

WANG Zhanyou，XIE Shunyi.Design of fuzzy controller for improving torque performance of brushless DC motor［J］.Electric Machines and Control，2009，13(6):913 －918.

［17］ 彭书华，李华德，苏中，等.不确定参数电动舵机滑模变结构控制［J］.电机与控制学报，2009，13(1):128 －132.

PENG Shuhua，LI Huade，SU Zhong，et al.Sliding mode varable structure control of electric steering engine with uncerta in parameters［J］.Electric Machines and Control，2009，13(1):128－132.