耦合电抗器在并联型三相并网逆变器中的应用

李瑞， 徐殿国， 徐壮， 苏勋文

(哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨150001)

0 引言

随着人们环保意识的增强及能源的日益紧缺，以风能、太阳能等为代表的新能源产业得到了长足的发展［1－2］。为了将由风能、太阳能等转换而来的电能输送到电网，通常需要由并网逆变器将其转换为幅值、频率、相位与电网相一致的电能，从而实现系统的并网运行［3－6］。为了提高并网逆变器的功率等级，同时降低生产成本，并提高系统可靠性，逆变器的并联运行得到了广泛关注［7－10］，为解决其中存在的环流问题，国内外学者进行了深入研究［11－12］。

传统上，通常采用交流侧使用隔离变压器方案或适当软件方案以抑制零序环流。文献［13］将多个结构相同的变换器并联使用，交流侧通过隔离变压器将各变换器的输入隔离起来，提高了变换器的功率等级，消除了零序环流问题，但隔离变压器的使用大大增加了系统的体积、重量和成本。文献［14］提出了并联型永磁直驱风电变流器拓扑结构，交流侧省去了隔离变压器，同时设计了零序环流器控制器，抑制了零序环流，大大提高了风电变流器的功率等级，但由于零序环流阻抗较小，因此零序环流问题解决起来难度相对较大，此外，零序环流控制器的使用增加了控制系统的复杂性。由于上述方案均存在自身问题，采用耦合电抗器的并联方案逐渐得到了人们的关注。首先，耦合电抗器只对并联变换器分支电流的差模分量具有阻尼作用，对其共模分量并无阻尼作用，因此它具有自主均流作用［15］，从而使各并联变换器电流应力趋于一致，为提升变换器的功率等级打下基础。同时，在理想情况下两并联逆变器分支电流相等，对于异侧并联的耦合电抗器而言不产生磁通，因此与传统电抗器相比，耦合电抗器的体积可大大减小［16］。此外，耦合电抗器可以实现对零序环流的抑制，文献［16］和［17］分别分析了移相角对并联型脉宽调制(pulse width modulation，PWM)整流器交流侧和直流侧无源元件的影响，并指出通过耦合电抗器可减小零序环流，但并未分析耦合电抗器抑制零序环流的根本原理。

针对上述问题，本文提出了一种由耦合电抗器组成的新型并联型三相并网逆变器，得出了它的去耦等效电路，并分别在三相静止坐标系和同步旋转坐标系下建立了平均模型，阐明了耦合电抗器抑制零序环流的根本机理，解决了零序环流引起的不均流、波形畸变等问题，提高了系统的可靠性和效率。最后，对一组1.5 MW三相并网逆变器进行了仿真验证，结果证明了上述分析及控制策略的正确性。

1 系统结构

本文所采用的系统结构如图1所示。前级输送的电能经直流母线电容C滤波、储能和稳压后，送入后级并联型三相并网逆变器。桥臂A1、B1、C1组成并网逆变器1，桥臂A2、B2、C2组成并网逆变器2，并网逆变器1、2相互并联，它们的交流输出分别经电感Lk1和Lk2(k=a，b，c)后连接到一起，进而接入电网。电感Lk1和Lk2之间存在耦合，互感为Mk(k=a，b，c)，且为异侧并联电路;Rak、Rbk、Rck(k=1，2)分别为并网逆变器1、2包含电感电阻在内的每相线路电阻;Udc为直流母线电压。

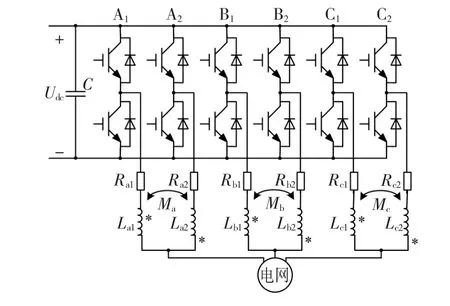
图1 系统拓扑结构Fig.1 Topology structure of the system

2 模型分析

2.1 去耦等效电路

为了对并联型三相并网逆变器进行分析，需要对耦合电抗器去耦，从而得到并网逆变器的去耦等效电路，如图 2 所示，图中 L′ak=Lak+Ma、L′bk=Lbk+Mb、L′ck=Lck+Mc(k=1，2)，且通常取 Lak=Lbk=Lck=Lk，Rak=Rbk=Rck=Rk(k=1，2)，Ma=Mb=Mc=M;il为前级所传送的直流电流;iak、ibk、ick(k=1，2)分别为并网逆变器1、2的三相并网分支电流;ea、eb、ec分别为电网三相电压。

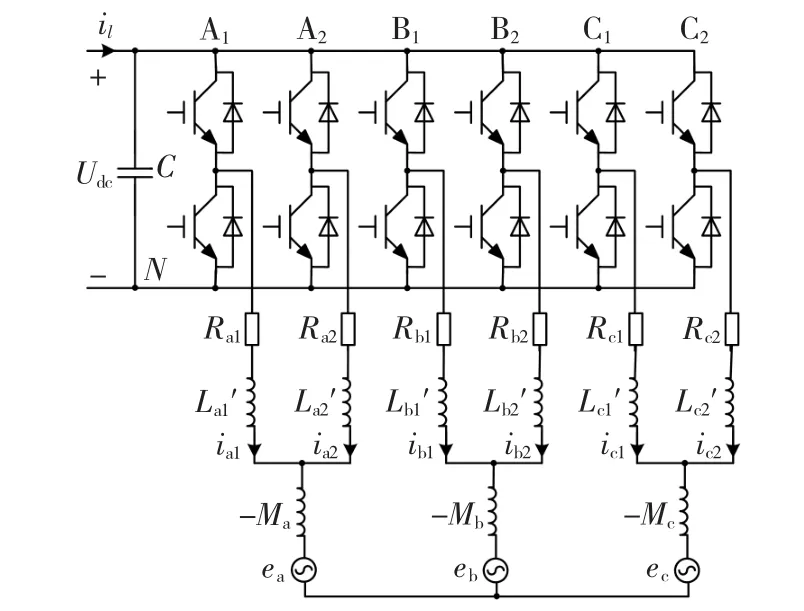
图2 去耦等效电路Fig.2 Decoupling equivalent circuit

2.2 三相静止坐标系下平均模型

根据每相桥臂的平均模型［14］，由基尔霍夫电压、电流定律可以得到由占空比表示的并联型三相并网逆变器的数学模型:

式中:L′k=L′ak=L′bk=L′ck(k=1，2);dak、dbk、dck(k=1，2)分别为并网逆变器1、2的三相桥臂占空比;UNO为负直流母线N与电网电压中性点O之间的电压;ia、ib、ic为三相总电流，即

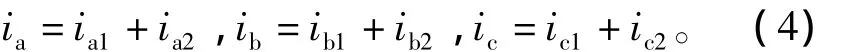
2.3 同步旋转坐标系下平均模型

在设计控制系统时，通常需要进行坐标变换，将三相静止坐标系下的时变交流量转换为同步旋转坐标系下的直流量，从而简化控制器的设计。根据等幅值原则，坐标变换矩阵为［14］

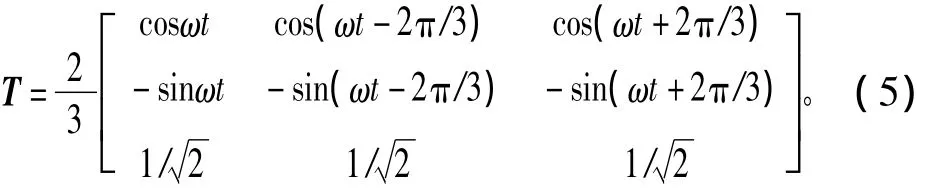
式中:ω为电网同步角速度。三相静止坐标系下物理量和同步旋转坐标系下物理量的关系可表示为

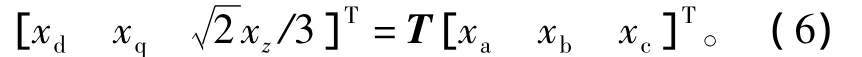
根据式(1)～式(3)描述的三相静止坐标系下并联型三相并网逆变器的平均模型，可以得到同步旋转坐标系下的平均模型，即

式中:

由式(7)～式(10)可以得到并联型三相并网逆变器的等效电路，如图3所示。可以看出，d轴电流分量id1、id2通过电感－M及受控电压源(－ωMiq)耦合到一起，这增加了控制的难度。由于d轴、q轴具有对称性，因此对于q轴电流分量可以得出似结论。从图中z轴等效电路可以看出，零序环流阻抗为(L1+L2+R1+R2+2M)，而采用普通三相电抗器时零序环流阻抗仅为(L1+L2+R1+R2)［14］，因此采用耦合电抗器时零序环流阻抗较大，起到了抑制零序环流的作用，尤其对高频零序环流效果更为明显。它的使用省去了交流侧笨重的隔离变压器及复杂的零序环流控制器，降低了生产成本，减小了并网逆变器的体积、重量，并简化了控制系统的设计，提升了并网逆变器的性能。

图3 同步旋转坐标系下等效电路Fig.3 Equivalent circuit in the synchronous rotating coordinates

定义izs为并联型三相并网逆变器的系统零序环流，且

则零序环流可以进一步分别表示为

3 系统控制策略

根据同步旋转坐标系下并联型三相并网逆变器的平均模型，设计了控制策略，如图4所示。

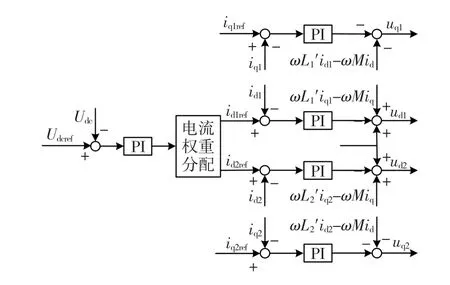
图4 系统控制策略Fig.4 Control strategy of the system

并网逆变器1、2使用共同的电压外环、独立的电流内环。电压环的作用主要是维持直流母线电压的稳定，从而使能量从直流侧输送到电网，它的输出经电流权重分配后，分别作为并网逆变器1、2的d轴电流给定id1ref、id2ref。在逆变器容量一定的情况下，为最大地将能量输送到电网，两逆变器q轴电流给定iq1ref、iq2ref一般设为零，从而实现单位功率因数并网。

由于通常并网逆变器1、2之间存在对称性，且电流环d轴、q轴分量之间也存在对称性，因此并网逆变器1、2的d轴、q轴电流环控制器可使用相同的控制参数。由于耦合电抗器的使用，使得并网逆变器1、2之间互相耦合，且对每个并网逆变器来说，d轴、q轴分量之间也存在相互耦合，为消除这些影响，在设计电流环时需采用前馈解耦控制策略。以并网逆变器1的d轴电流环控制器为例，将解耦项(ωL′1iq1－ωMiq)补偿到PI调节器的输出，即可以起到并网逆变器1、2之间解耦的作用，又可以使电流环d轴、q轴分量之间实现解耦。此外，电网电压d轴前馈分量ed抵消了实际中电网电压的影响，进而得到并网逆变器1的d轴输出参考电压ud1。得到d轴、q轴输出参考电压后，经坐标反变换送入SVPWM模块，进而得到三相占空比信号，从而实现对并网逆变器的控制。

4 仿真分析

为了验证上述模型及控制策略的正确性，本文对一组1.5 MW并联型三相并网逆变器进行了仿真验证，并将采用普通电抗器与采用耦合电抗器两种情况进行了对比，以更好地突出耦合电抗器在并联型三相并网逆变器中的作用。仿真采用690 V电网系统，即ea=eb=ec=690 V;由于1.5 MW并网逆变器多采用1 700 V电压等级IGBT，考虑到IGBT耐压能力，同时防止出现过调制，调制方式采用 SVPWM，直流母线电压取为1 100 V，即Udc=1100 V;直流母线电容 C=6 800 μF;L1=L2=200 μH;考虑到零序环流抑制以及两并网逆变器的控制效果，取耦合系数k为0.415，则互感

图5为两并网逆变器的零序环流仿真波形。从图5(a)可以看出，采用普通电抗器时零序环流严重，峰值几乎达到了500 A。从图5(b)可以看出，采用耦合电抗器时零序环流大大减小。零序环流的大小受两并网逆变器之间参数一致性的影响，如电感值、IGBT开关特性等参数的影响，通过改善参数一致性可进一步减小零序环流。从图中还可以看出，两零序环流iz1、iz2大小相等、方向相反。

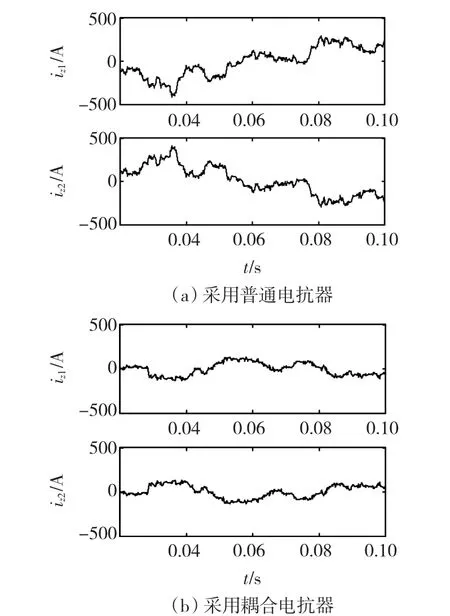
图5 两并网逆变器的零序环流波形Fig.5 Zero-sequence circulating currents of two grid-connected inverters

图6为两并网逆变器的a相分支电流波形。从图6(a)可以看出，采用普通电抗器时两分支电流存在波形不一致、畸变等问题。从图6(b)可以看出，采用耦合电抗器时两分支电流一致性良好，且波形正弦。但是由于耦合电抗器的使用，使得两并联逆变器之间存在耦合，这在一定程度上会对电流总谐波畸变率(total harmonic distortion，THD)产生负面影响，但总体而言，由于耦合电抗器降低了波形畸变等问题，电流THD还是降低了，从而降低了系统对电网的谐波污染。

图6 两并网逆变器的a相分支电流波形Fig.6 Phase a branch currents of two grid-connected inverters

图7为并网逆变器1的三相分支电流仿真波形。从图7(a)可以看出，采用普通电抗器时三相电流存在畸变、不对称等问题。从图7(b)可以看出，耦合电抗器的使用减轻了三相电流畸变、不对称等问题。

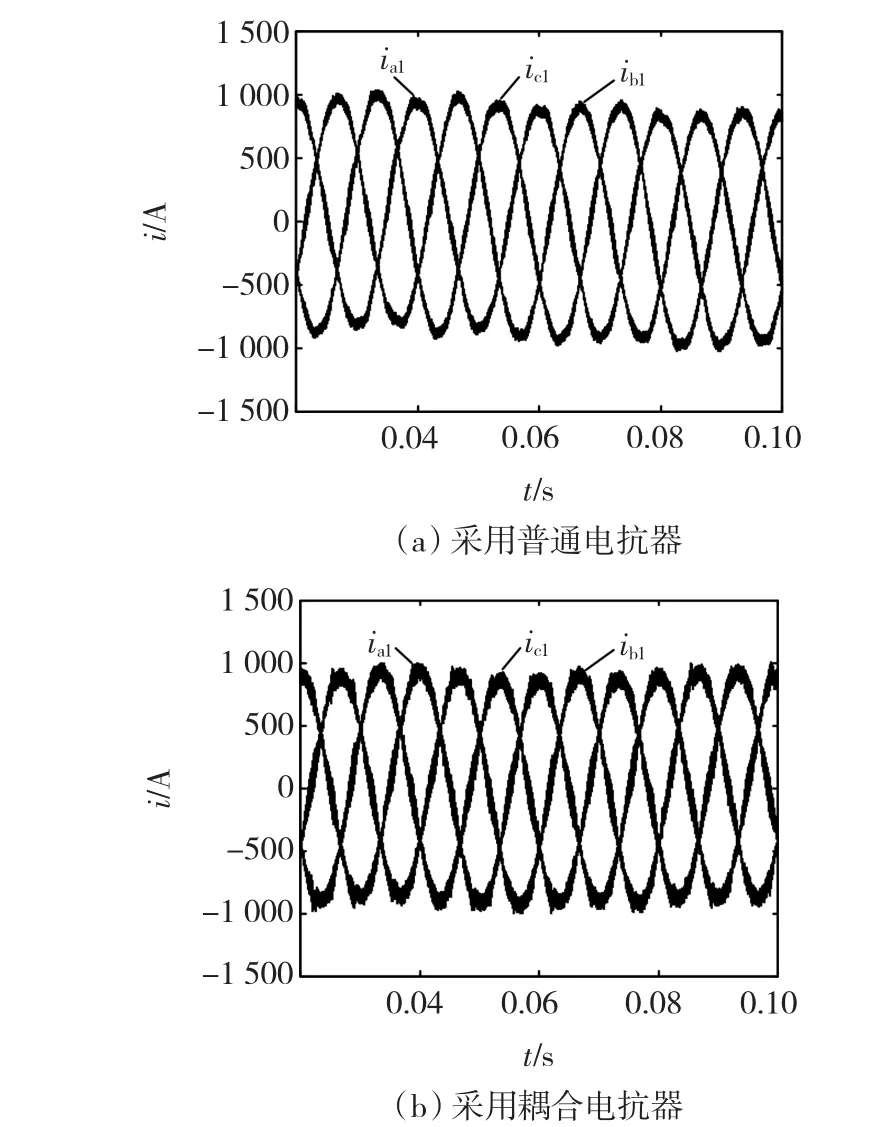
图7 并网逆变器1的三相分支电流波形Fig.7 Three-phase branch currents of grid-connected inverter 1

图8为采用耦合电抗器时并联型并网逆变器的三相总电流波形及电网电压、电流相位关系，从图8(a)可以看出，总电流波形三相对称、正弦性良好。图8(b)为采用耦合电抗器时电网电压、电流相位关系，可以看出，电网电压与电流相位相差180°，系统工作在单位功率因数逆变状态。

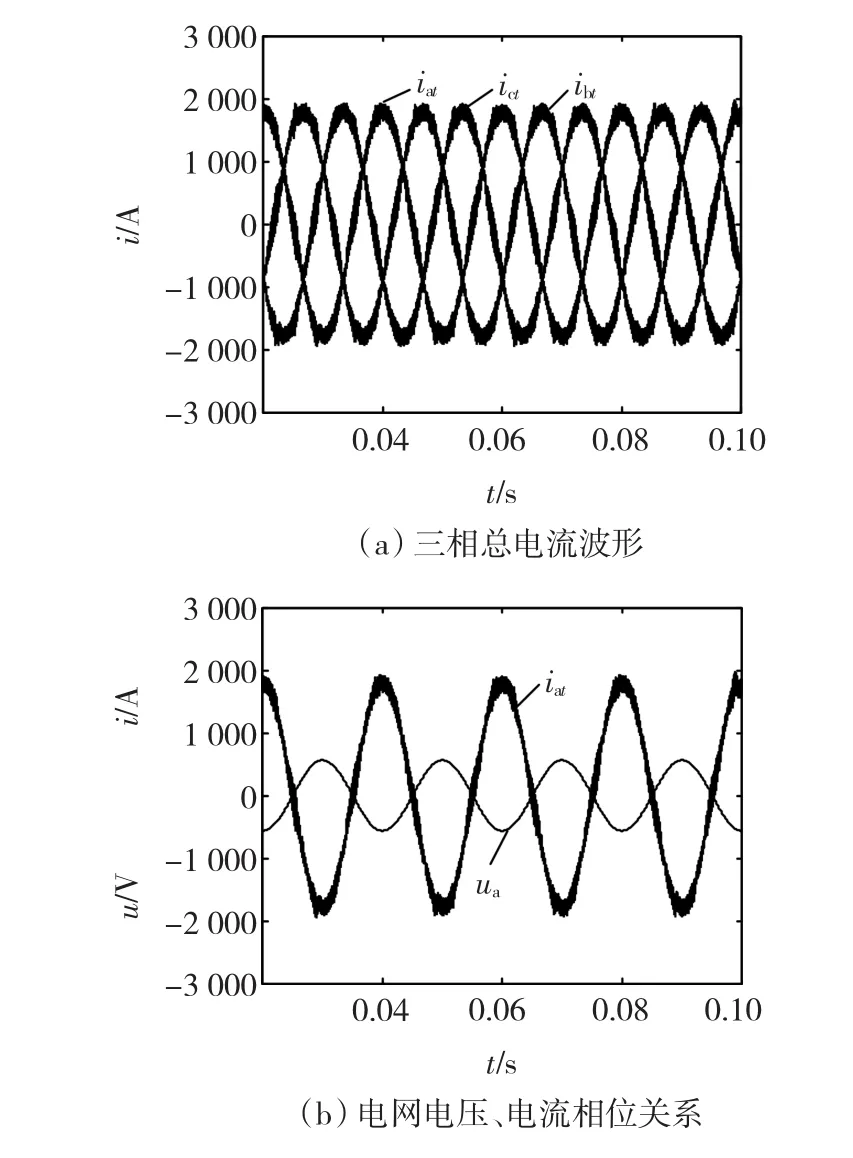
图8 采用耦合电抗器时三相总电流波形及电网电压、电流相位关系Fig.8 Three-phase total currents and phase-relationship between grid voltage and current using interphase inductors

5 结论

本文通过对由耦合电抗器组成的新型并联型三相并网逆变器的研究，得出了它的去耦等效电路及平均模型，阐明了耦合电抗器抑制零序环流的根本机理，即采用耦合电抗器时并联型三相并网逆变器的零序环流阻抗大于采用普通三相电抗器时的零序环流阻抗，因此耦合电抗器的使用可以对零序环流起到抑制作用，解决了零序环流引起的不均流、波形畸变等问题，提高了系统的可靠性和效率，从而为生产更高功率等级的并网逆变器产品奠定了基础。

［1］ GABE I J，MONTAGNER V F，PINHEIRO H.Design and implementation of a robust current controller for VSI connected to thegrid through an LCL filter［J］.IEEE Transactions on Power Electronics，2009，24(6):1444－1452.

［2］ 王继东，朱雪玲，苏海滨，等.三相光伏并网Z－源逆变器的比例谐振控制［J］.电机与控制学报，2010，14(4):86－91.

WANG Jidong，ZHU Xueling，SU Haibin，et al.Proportional-resonant control for Z-source inverter in three-phase PV grid-connected system［J］.Electric Machines and Control，2010，14(4):86－91.

［3］ SERPA L A，PONNALURI S，BARBOSA P M，etc.A modified direct power control strategy allowing the connection of three-phase inverters to the grid through LCL filters［J］.IEEE Transactions on Industry Applications，2007，43(5):1388 －1400.

［4］ 胡雪峰，龚春英，陈新.采用垂直多载波调制技术的并网逆变器［J］.电机与控制学报，2011，15(7):60－64，70.

HU Xuefeng，GONG Chunying，CHEN Xin.A grid-connected inverter based on vertical layered multi-carrier modulation strategy［J］.Electric Machines and Control，2011，15(7):60 －64，70.

［5］ LOH P C，HOLMES D G.Analysis of multiloop control strategies for LC/CL/LCL-filtered voltage-source and current-source inverters［J］.IEEE Transactions on Industry Applications，2005，41(2):644－654.

［6］ 邓翔，胡雪峰，龚春英.LCL滤波并网逆变电源的控制策略研究［J］.电机与控制学报，2011，15(5):37－41.

DENG Xiang，HU Xuefeng，GONG Chunying.Study on control scheme for grid-connected inverter with LCL filter［J］.Electric Machines and Control，2011，15(5):37 －41.

［7］ PRODANOVIC M，GREEN C T.Control and filter design of three-phase inverters for high power quality grid connection［J］.IEEE Transactions on Power Electronics，2003，18(1):373－380.

［8］ 汪洪亮，岳秀梅，裴雪军，等.逆变器并联系统的新功率算法及实现［J］.电机与控制学报，2010，14(5):37－43.

WANG Hongliang，YUE Xiumei，PEI Xuejun.New power calculation method and realization of parallel inverters［J］.Electric Machines and Control，2010，14(5):37 －43.

［9］ 于玮，徐德鸿.基于虚拟阻抗的不间断电源并联系统均流控制［J］.中国电机工程学报，2009，29(24):32－39.

YU Wei，XU Dehong.Control scheme of parallel UPS system based on output virtual resistance［J］.Proceeding of the CSEE，2009，29(24):32－39.

［10］ 李立，黄松柏，汪洪亮.基于电压/电流控制模式的组合式三相逆变器［J］.电机与控制学报，2011，15(2):63－70.

LI Li，HUANG Songbai，WANG Hongliang.Combined three －phase inverter operating in voltage or current controlmode ［J］.Electric Machines and Control，2011，15(2):63 －70.

［11］ 毛惠丰，陈增禄.SPWM多重化并联逆变器的死区效应补偿方法的研究［J］.电力电子技术，2004，4(3):49－55.

MAO Huifeng，CHEN Zenglu.Analysis for compensation of dead-time effects for multiple-SPWM inverters in parallel［J］.Power Electronics，2004，4(3):49－55.

［12］ 魏永清，张晓锋，乔鸣忠.采用参考电压调节的并联逆变器控制技术［J］.电机与控制学报，2011，15(2):84－88.

WEI Yongqing，ZHANG Xiaofeng，QIAO Mingzhong.Parallel control technique ofmultiple inverters based reference voltage regulation［J］.Electric Machines and Control，2011，15(2):84－88.

［13］ Dixon J W，Ooi B T.Series and parallel operation of hysteresis current-controlled PWM rectifiers［J］.IEEE Transaction on Industry Applications，1989，25(4):644 －651.

［14］ 李瑞，徐壮，徐殿国.并联型永磁直驱风电系统的环流分析及其控制［J］.中国电机工程学报，2011，31(6):38－45.

LI Rui，XU Zhuang，XU Dianguo.Analysis and control of circulating current in parallel permanent-magnet-direct-drive wind power system［J］.Proceeding of the CSEE，2011，31(6):38 －45.

［15］ INGYU Park，SEONIK Kim.Modeling and analysis of multi-interphase transformers for connecting plural power converters in parallel［C］.Power Electronics Specialists Conference.St.Louis，USA，1997:1164－1170.

［16］ DI Zhang，FRED Wang，ROLANDO Burgos，et al.Impact of interleaving on AC passive components of paralleled three-phase voltage-source converters［J］.IEEE Transactions on Industry Applications，2010，46(3):1042－1054.

［17］ DI Zhang，FRED Wang，ROLANDO Burgos，et al.DC-link ripple current reduction for paralleled three-phase voltage-source converters with interleaving［J］.IEEE Transactions on Power E-lectronics，2011，26(6):1741 －1753.