机器人灵巧手柔性关节自适应阻抗控制

樊绍巍， 宗华， 邱景辉， 陈兆芃

(1.哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江哈尔滨150001;2.哈尔滨工业大学电子与信息工程学院，黑龙江哈尔滨150001;3.德国宇航中心机器人与系统动力学研究所，慕尼黑韦斯林82230)

0 引言

多指仿人灵巧手的研究是类人型机器人中的难点，也是实现仿人机器人灵巧操作的关键系统。近年来高集成度高性能灵巧手的出现对控制系统提出了更高要求［1-5］。特别是同步齿形带、绳索及微型谐波减速器的引入，在有效减小机器人体积的同时，引入的关节柔性也得到了许多研究者的注意。在Sweet和Good等人阐述了关节柔性对机器人的控制性能的影响［6-7］后，Spong建立了柔性机器人关节模型［8］。随后出现了一些典型柔性控制方法［9-11］，尽管上述的控制策略验证了理论的有效性，但实际应用不尽理想。针对上述问题，Albu-Schaer和Hirzinger开发了具有非线性摩擦补偿的PD控制器，并通过实验证明了该控制器在柔性关节机器人上的有效性［12］。为了避免上述方法高增益项的不稳定性，Albu-Shaer和Ott等人提出基于无源性控制的方法，该方法针对具有关节力矩反馈的柔性关节机器人进行了深入的研究和大量的实验分析［13-15］。

上述研究尽管考虑了关节的柔性补偿问题，但对于关节中的非线性摩擦力没有进行深入研究。针对基于关节力矩控制的机器人灵巧手来说，其关节的高集成度设计和小范围精细操作的任务要求，非线性摩擦力对其控制稳定性的影响也显现出来，因此在考虑关节柔性的同时，不得不对其关节摩擦力进行补偿。通常针对摩擦力的不确定性，许多研究者采用了基于干扰观测器的方式进行具有摩擦力补偿的机器人控制的补偿方法［16-18］，结合 HIT/DLR Hand II五指灵巧手各手指关节摩擦力的不确定性的特点，提出一种具有自适应补偿摩擦力的阻抗控制策略显得尤为重要。

建立了具有柔性关节的HIT/DLR II灵巧手控制模型，并在灵巧手中实现了基于关节力矩的阻抗控制器，提出了基于扩展卡尔曼滤波器的自适应摩擦力观测器和基于最小二乘法的重力优化补偿策略，以实现灵巧手控制系统的自适应性，提高稳定性和准确性。

1 HIT/DLR II型灵巧手控制模型

HIT/DLR II型五指灵巧手如图1所示。HIT/DLR II型五指灵巧手的传动系统为同步齿形带结合谐波减速器的形式，这种传动方式的关节柔性远大于关节间杆件的柔性。以手指末端关节2为例，其关节柔性可由刚度为k的弹簧表示，如图2所示。机器人手指其他关节模型与之相同。

图1 HIT/DLR II五指仿人灵巧手Fig.1 Five-fingered anthropomorphic dexterous robot hand HIT/DLR II

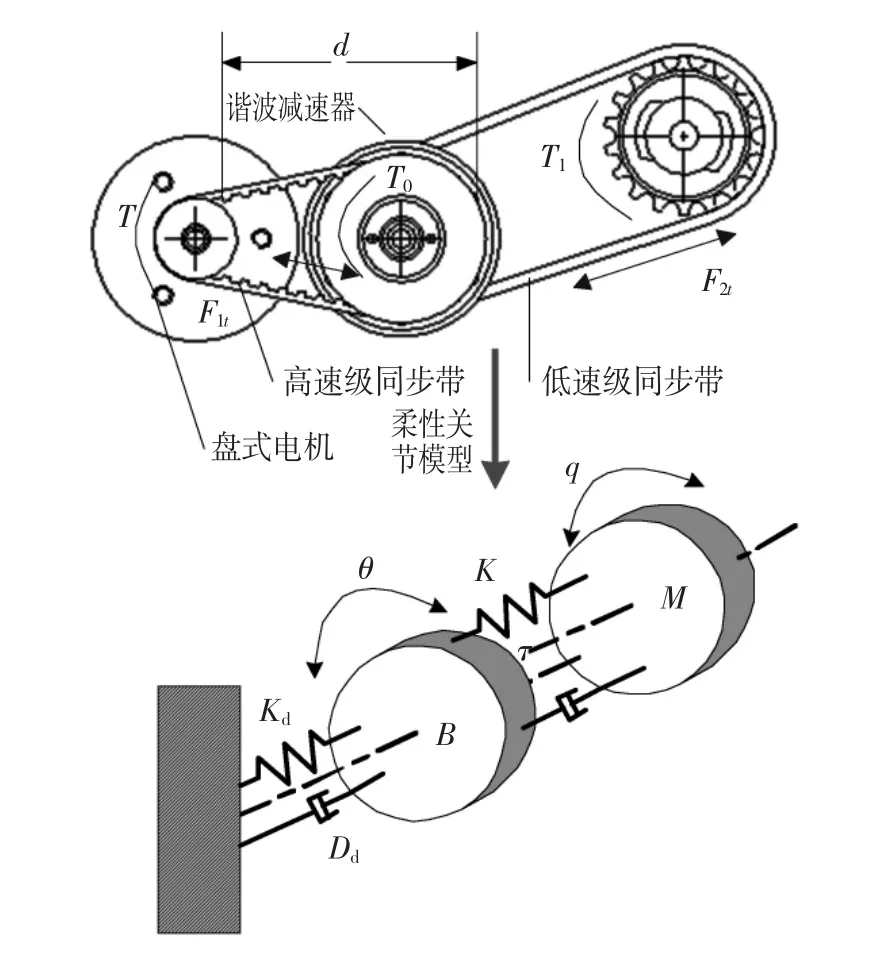
图2 灵巧手柔性单关节及其模型Fig.2 Single flexible joint of robot finger and modeling

柔性机器人灵巧手单关节动力学［19］可表示为

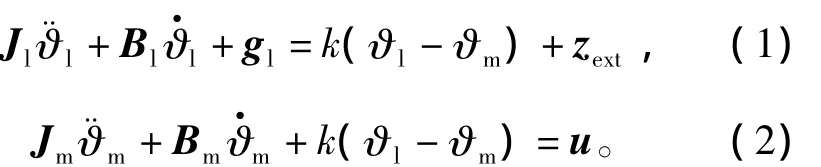
其中:ϑl，ϑm分别为经过传动比1/n换算的关节位位置和电机位置;zext为关节所受外力矩;Jm和Jl分别为电机和关节端的惯量;Bm，Bl，Jm，Jl分别为电机及关节端粘滞摩擦系数和惯量;gl为重力。基关节(关节0，1)俯仰和侧摆两个自由度所采用的如图3所示的差动耦合机构的机器人模型可表示为

其中:θl为差分耦合机构之前的关节端位置;θq为差分耦合机构之后的的关节端位置，可用q表示;灵巧手手指中有一个差分耦合关节，因此q∈R3;τ为关节端力矩;τl为差分耦合机构之前的关节端力矩。完整的机器人灵巧手手指动力学模型为

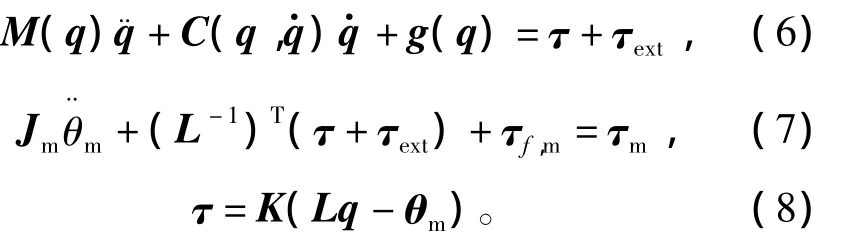
式中:M(q)，C(q)和g(q)分别为惯量矩阵，离心力项和重力项;关节力矩由K(Lq-θm)表示;θm为经过传动比1/n的电机位置;L为差分耦合齿轮变换矩阵;q为关节端位置;K，Jm分别为包含柔性关节刚度系数的对角矩阵和乘以传动比平方的电机惯量;τext和 τf，m分别为在关节空间的广义外力向量和摩擦力向量;驱动器广义力矩τm在控制器中为控制输入。机器人手指各关节的坐标系建立和DH参数分别如图4和表1所示。

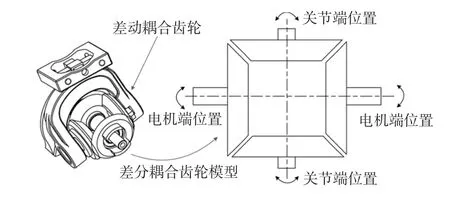
图3 基关节差分耦合机构及其模型Fig.3 Differential bevel gears and modeling

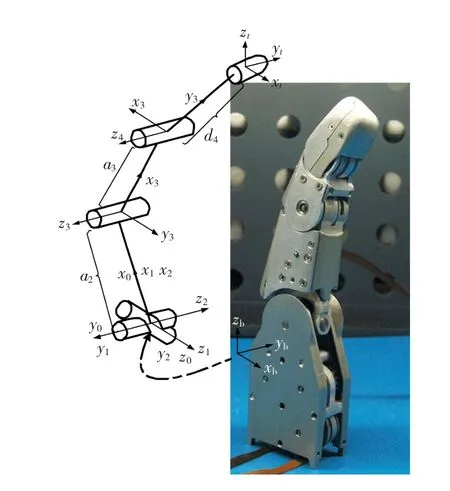
图4 手指关节坐标系建立Fig.4 Frame assignments and parameters in robot finger

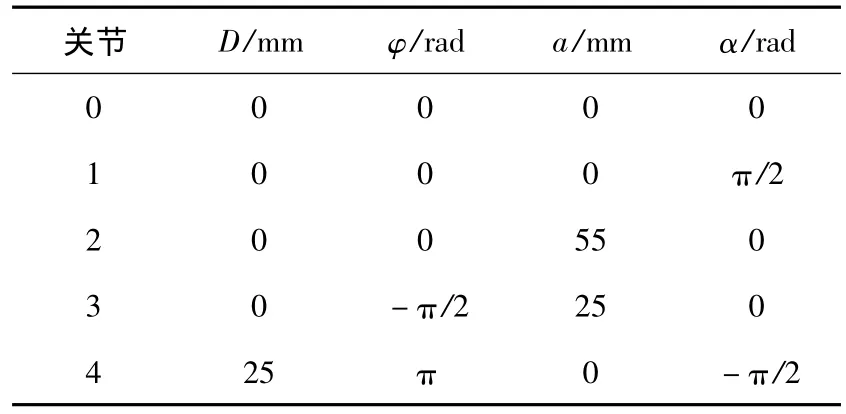
表1 HIT/DLR II型灵巧手DH参数Table 1 DH parameters of HIT/DLR Hand II

2 柔性关节机器人灵巧手阻抗控制

2.1 关节空间阻抗控制

机器人的目标阻抗模型可由质量-弹簧-阻尼机构来描述，如图2所示。其中Kd和Dd分别为弹簧-阻尼系统的刚度系数和阻尼系数。考虑关节柔性的影响，基于关节力矩的阻抗控制使电机转动惯量表面上减小，从而使阻抗控制的柔顺性更为有效［20］。式(7)可在关节空间中变换为

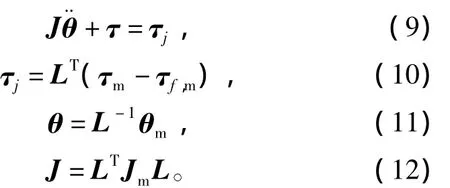
使用一个新的控制输入u，即

式中:Jc为对角正定矩阵，且该矩阵中jci＜ji。由此可知，电机实际惯量从J减小到了表面惯量Jc，即

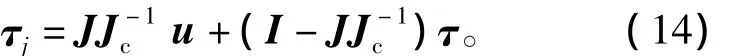
表面惯量的减小将提高阻抗控制柔顺性能。实际惯量和表面惯量的比率JmJ-1c在应用中由HIT/DLR II型灵巧手中关节力矩传感器的噪声决定。在高刚度阻抗控制中，这个比率应该取比较小的值。

基于无源控制的思想，关节空间阻抗控制可以采用基于电机位置的PD型控制器，即

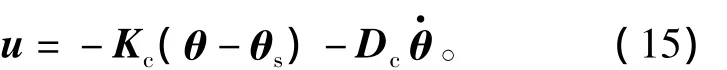
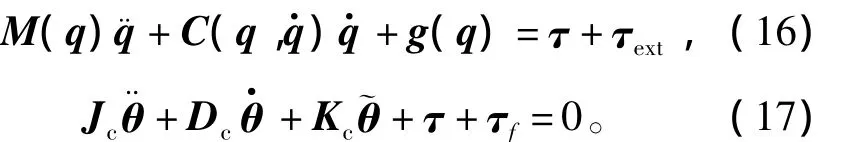
2.2 笛卡尔空间阻抗控制

机器人灵巧手末端操作器位置和姿态可由一组笛卡尔空间局部坐标x∈Rm来表示。x与机器人关节位姿坐标向量q∈Q的关系描述为x=f(q)，f:Q→Rm，即机器人正运动学。由微分运动学雅可比矩阵J(q)=∂f(q)/∂q可以得到机器人的笛卡尔空间速度和加速度为

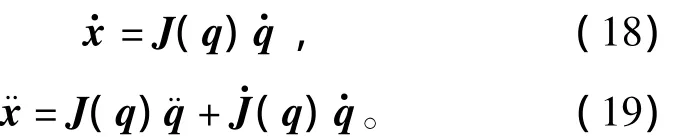
由于机器人灵巧手工作空间均为手指非奇异位置，因此J(q)为满秩矩阵。引入位置误差～x=xxd，其中xd为虚拟稳态点坐标，在机器人运动过程中为时变量。笛卡尔空间阻抗控制器设计的目标是基于系统动力学方程(6)，使作用在灵巧手末端的广义外力/力矩Fext∈Rm和位置误差～x满足以下目标阻抗关系，即

其中，Λd，Dd和Kd分别为目标阻抗关系中的对称正定惯量矩阵，阻尼系数矩阵和刚度系数矩阵。作用在灵巧手末端操作器上的广义外力可在关节空间中表示为

由式(18)和式(19)可以得到

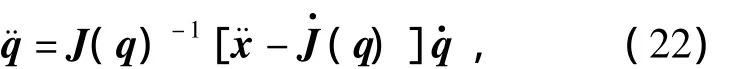
将其代入式(6)可得

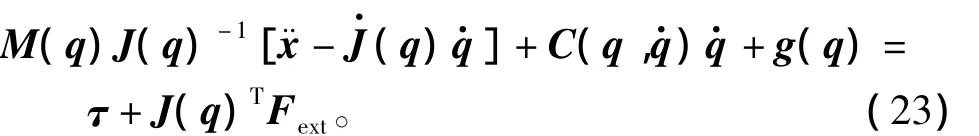
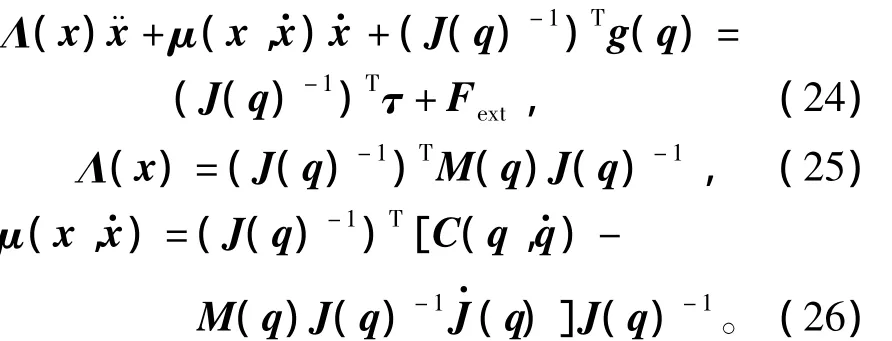
其中，q=f-1(x)，并且=J［f-1(x)］。

将关节空间中的重力力矩g(q)和关节力矩τ在笛卡尔空间中表示为Fg(x)和新的控制输入向量Fτ，整个系统动力学方程可以表示为

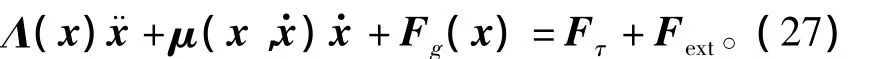
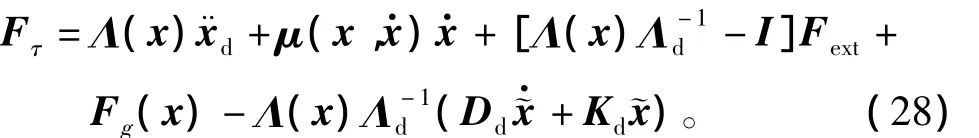
控制力矩τ可设计为

根据式(29)，式(28)可简化为

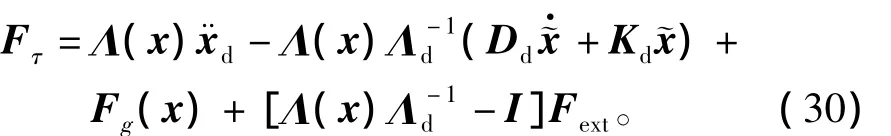
机器人灵巧手在进行操作时运行速度相对较低，离心力和科里奥利力项可以忽略不计。另外，目标阻抗关系中Λd可以设计为与机器人惯量矩阵Λ(x)相同，这样就在控制器设计中避免了外力/力矩项Fext。阻抗控制规律为

阻抗控制器输入力矩在关节空间中的表达式为

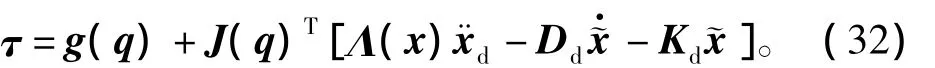
在正运动学x=f(q)中使用电机位置向量θ代替关节端位置向量q，基于PD内环位置控制的灵巧手笛卡尔空间阻抗控制器可以由式(33)的形式获得，反馈控制规律为

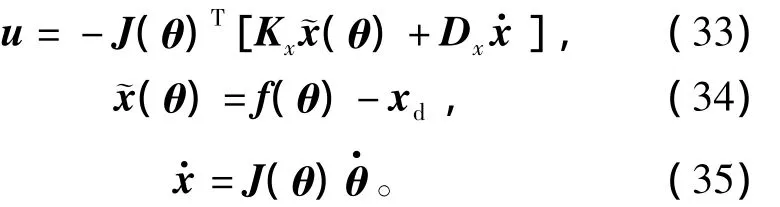
其中:Kx和Dx分别为阻抗控制刚度系数和阻尼系数矩阵，分别对应于式(32)中的Kd和Dd;xd为笛卡尔坐标系中电机的虚拟平衡位置。综合式(33)和式(14)，包含笛卡尔空间阻抗控制器的机器人灵巧手笛卡尔空间动力学闭环方程为

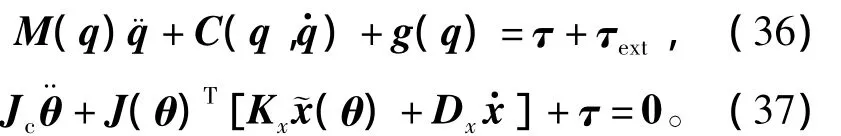
2.3 基于最小二乘法的最优化重力补偿

在基于PD位置控制的机器人阻抗控制策略中，可以使用电机位置进行准稳态的重力补偿。柔性关节机器人灵巧手中的重力表示为

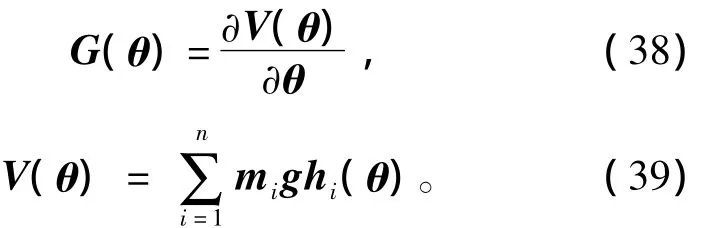
其中:V:Rn→R为机器人灵巧手手指的势能;θ为关节控制位置向量;hi为各个关节的重心。由于HIT/DLR II型灵巧手高度集成化的结构设计，关节与关节之间的界限没有明显划分，所以无法由从机构设计中精确获得各个关节的质量和重力。本文基于最小二乘法和正运动学实现了优化的手指重力补偿。式(38)可以重新写为

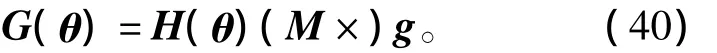
其中:H(θ)，g分别为基座坐标系中的质心坐标向量和重力向量;M为需要通过最小二乘法优化而获得的质量向量，即

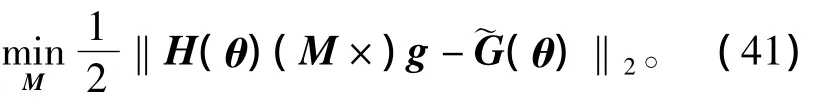
由文献［10］可知，机器人灵巧手的关节柔性，在刚度较低的情况下，关节端位置和电机位置可能会出现较大偏差，因此需要建立一个基于电机端位置的重力补偿量，以补偿机器人运动中关节端的重力。考虑准稳态位置点(外力/力矩τext=0)的集合Ω:={(q，θ)|K(θ -q)=g(q)}，重力补偿项(θ)可表示为

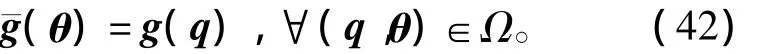
式(42)所表示的重力补偿项可由θ和q的关系确定。对于任意位置点(θ，q)∈Ω，电机位置可以由关节端位置唯一确定，即

由于h(q)的反函数存在，而且映射T(q):=θ-K-1g(q)为压缩映射，因此由压缩映射定理可知，迭代式

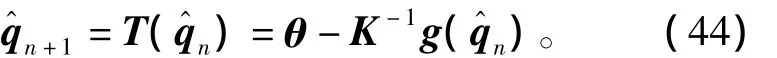
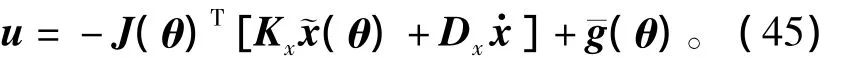
3 基于扩展卡尔曼滤波器的自适应摩擦力补偿

非线性摩擦力补偿能够极大地提高阻抗控制中的位置精确度。机器人灵巧手中采用由静摩擦力和粘滞摩擦力组成的摩擦力模型，即

其中:b和c分别为粘滞摩擦力系数和静摩擦力系数。包含摩擦力的机器人动力学模型为

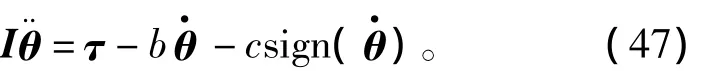
其中:τ=τm-τext;I为电机惯量。为实现包含摩擦力补偿的控制器，必须首先确定机器人灵巧手动力学模型中的各项参数。扩展卡尔曼滤波器是一种优化和估计策略，特别是当系统模型并不能够精确获得的时候，其优化和预测能力可以非常有效地协助控制器提高控制性能。扩展卡尔曼滤波器可分为预测和估算两个步骤［22］。基于当前状态和系统动力学模型，系统预测状态在卡尔曼滤波器的预测步骤中得出

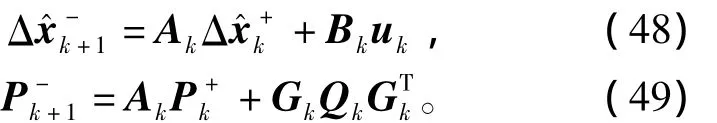
其中:Ak，Gk为系数矩阵;Qk为模型噪声的协方差。估算步骤通过比较预测步骤和测量的结果，得到优化的估算为

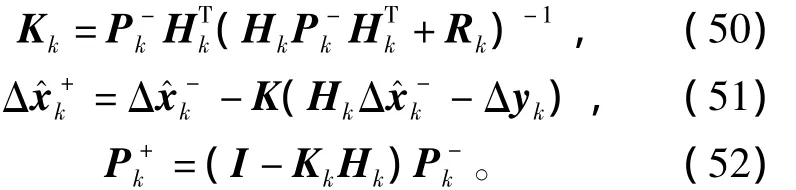
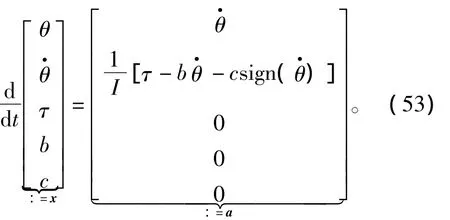
其中，I为电机转动惯量。由于摩擦力的关系，系统状态方程引入了非线性因素。将符号函数sign()线性化，可以得到

其中，ξ∈R→0。由此可以消除系统动力学方程中的非线性因素。对系统状态方程进行偏微分，然后使用符号Δ代替偏微分符号∂，线性化的系统动力学方程为

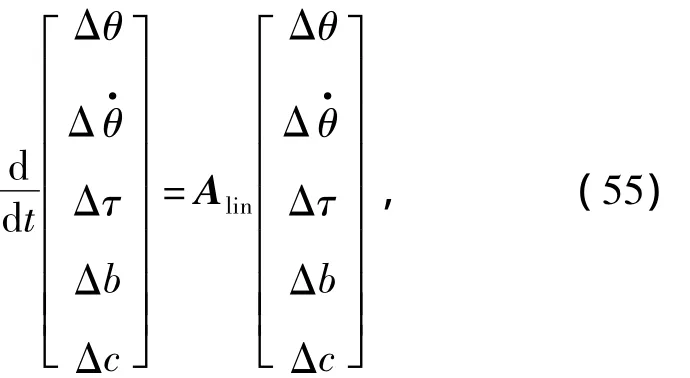
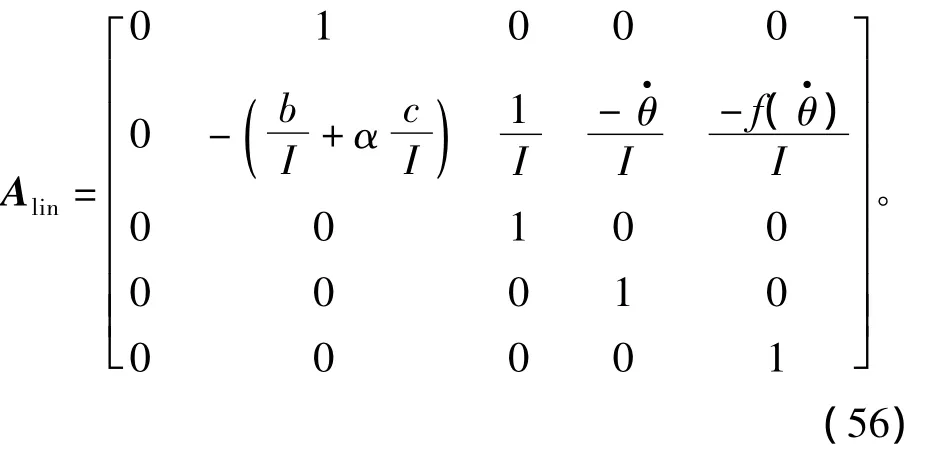
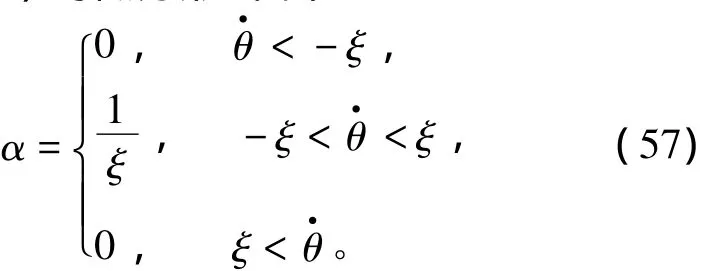
式(55)［23］的解可表示为

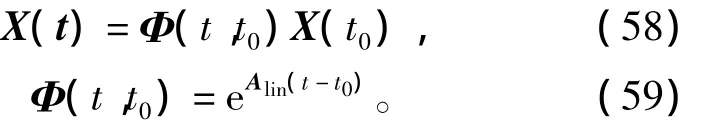
离散时间点取kts到(k+1)ts，将指数函数展开，得到式(55)在离散时间空间的解为

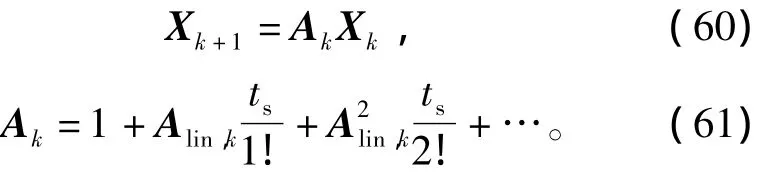
其中，Alin，k=Alin(x(kts))=Alin。结合式(56)，可以得到线性化自适应卡尔曼滤波器为

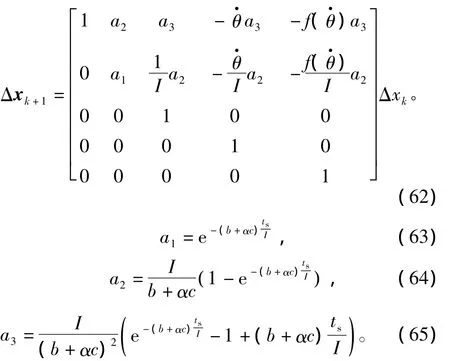
具有摩擦力补偿的笛卡尔空间自适应阻抗控制器为

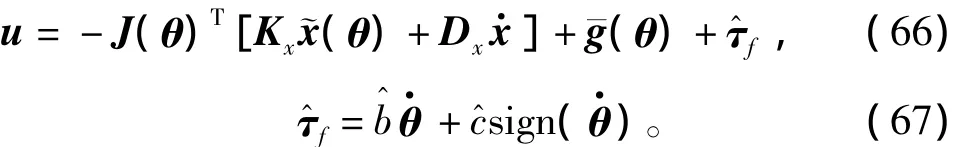
4 实验结果

4.1 摩擦力观测

基于扩展卡尔曼滤波器的粘滞摩擦力参数和静摩擦力参数观测实验结果如图5所示。其观测值收敛于由最小二乘法计算出的测量值(b=0.3，c=0.1)。模型线性化过程中必要的近似处理造成了如图5所示的稳态误差。实验结果验证了基于扩展卡尔曼滤波器的摩擦力观测有效性。系统噪声Q和测量噪声协方差R在卡尔曼滤波器的观测效果中起到了关键作用。观测器的效能可通过离线调整这两个卡尔曼滤波器参数来进一步提高。在摩擦力观测器中，关节速度θ·也是观测结果之一，因此速度观测的结果也间接证明了摩擦力观测器的有效性，如图6所示。

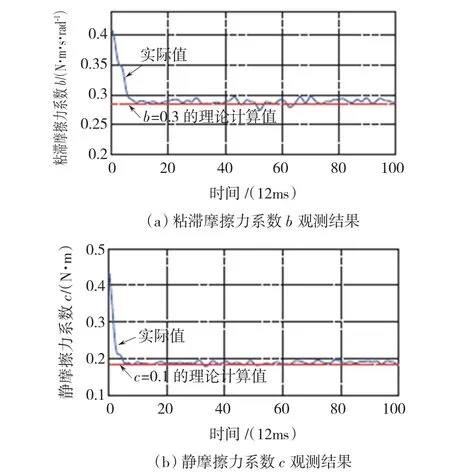
图5 基于EKF的摩擦力系数观测Fig.5 Friction parameter estimation with EKF

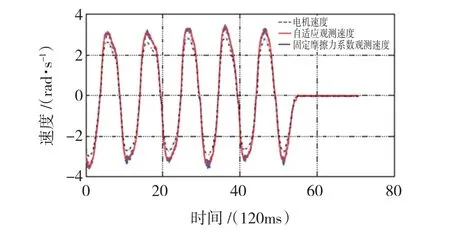
图6 基于EFK的速度观测结果Fig.6 Velocity estimation with EKF

4.2 关节空间阻抗控制和摩擦力自适应补偿

实验的第1部分验证了摩擦力补偿的有效性。手指各个关节独立驱动，手指末端关节2做周期性往复运动。具有摩擦力补偿和无摩擦力补偿的阻抗控制器轨迹跟踪实验结果如图7所示。实验结果表明，相同阻抗参数和实验条件时，具有自适应摩擦力补偿的阻抗控制器位置误差最大为0.8°，而无摩擦力补偿的阻抗控制器位置误差最大为2°，因此验证了摩擦力观测器的有效性。

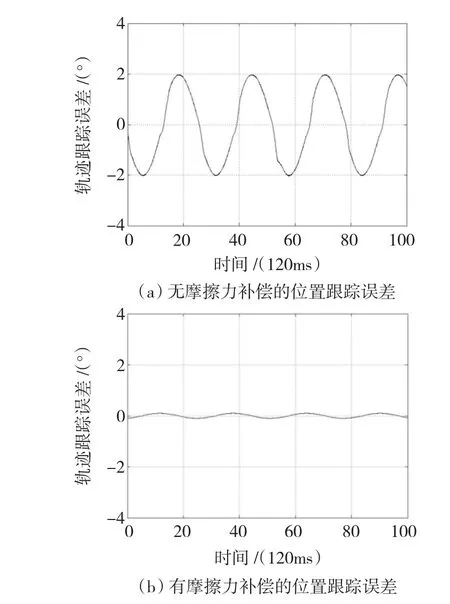
图7 摩擦力补偿位置跟踪实验Fig.7 Position tracking experiment with friction compensation

实验的第2部分中，手指受控制器驱动各个关机向不同方向运动，在到达目标位置之前与外界环境相接触。阻抗控制系数与第1部分实验相同。如图8所示，在关节空间阻抗实验中，手指3个关节(指尖关节，基关节俯仰，基关节侧摆)与外界环境相接触时的关节位姿为［28°，52°，17.5°］，手指关节位置在上述位置停止目标轨迹跟踪，开始进入阻抗运动模式。实验结果表明，在自由空间运动过程中，手指的各个关节能很好地跟踪目标轨迹，而在与外界环境接触的过程中，关节力矩保持衡定，如图9所示。由此可知灵巧手关节空间阻抗控制的有效性。以上两个实验中阻尼系数和刚度系数分别为:Dd=［0.001 3，0.001 3，0.003 1］(N·mm·s/°)，Kd=［0.062 5，0.062 5，0.125］(N·mm/°)

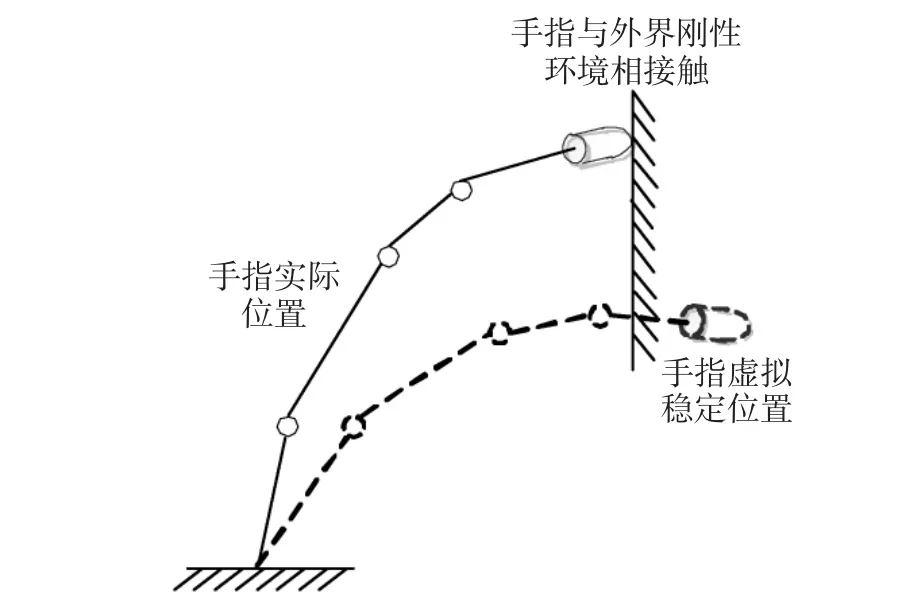
图8 机器人手指接触刚性环境Fig.8 Robot finger contacts with external rigid object

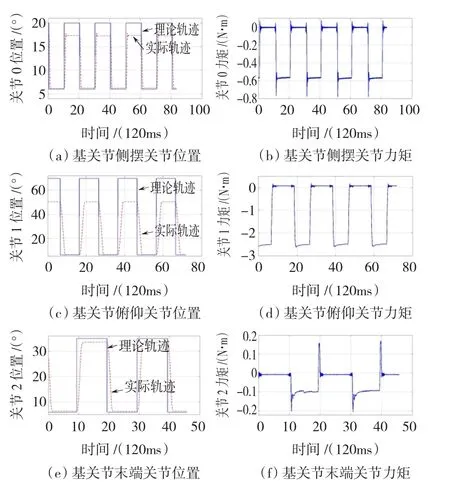
图9 手指3个关节的位置轨迹追踪和关节力矩结果Fig.9 Position tracking and torque response in 3 joints of the finger

4.3 笛卡尔空间阻抗控制

为进行笛卡尔空间阻抗控制，首先需要确定控制参数Kx和 Dx，以及惯量矩阵 Λ(x)和重力项g()。惯量矩阵Λ(x)和重力项g(¯)由灵巧手的机械设计参数根据第3节中的方法得出。而控制参数Kx和Dx可根据双对角化法，由惯量矩阵和设计阻尼比率得到。

笛卡尔空间阻抗控制实验中，使用了灵巧手5个模块化手指中的1个手指，其他4个手指处于制动状态。如图10所示，实验中驱动手指跟踪目标轨迹(红色虚线表示)运动，手指的实际运动轨迹如实线所示。手指在Δx=0.011 5 m处于外界环境，x方向实际运动轨迹停止跟踪目标轨迹，进入阻抗运动模式。实验结果表明，在自由空间运动过程中，手指笛卡尔空间坐标轨迹能够很好地跟踪目标轨迹。而在与刚性环境接触的过程中，笛卡尔空间接触力保持衡定。

在另一个笛卡尔空间阻抗控制实验中，机器人手指处于目标准稳态位置 xd=［0.036，0.036，0.2］。实验人员使用外力将手指朝不同方向拉动，然后释放手指。在笛卡尔空间阻抗控制器驱动下，机器人手指将克服摩擦力和重力回到准稳态位置xd。手指笛卡尔空间运动轨迹和力反应如图11所示。实验结果表明，具有摩擦力和重力补偿的笛卡尔空间阻抗控制策略在x，y和z 3个方向的稳态位置误差均在0.2 mm以内。实验的第2部分中，手指末端受x方向上的力在±x方向做往复运动。阻抗控制设计刚度Kx=1 300 N/m，Dx=12.5 N·s/m和测量刚度的比较结果如图12所示。上述实验结果表明所设计的笛卡尔空间阻抗控制器是有效的。

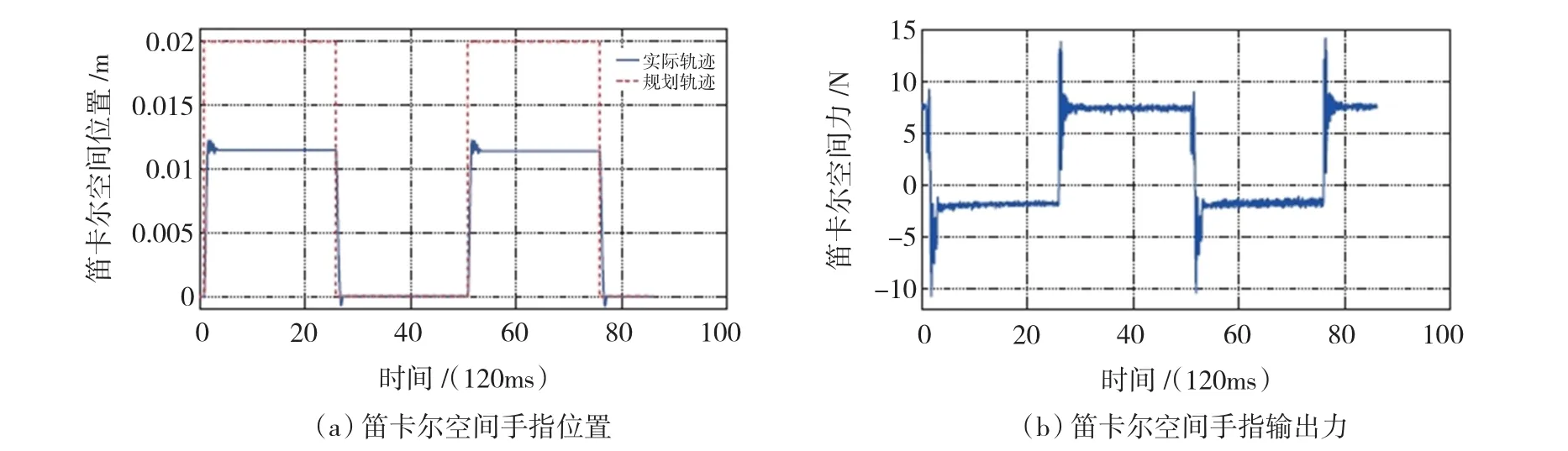
图10 手指与环境接触时笛卡尔空间位置和力跟踪Fig.10 Cartesian position tracking and force response with contacting environment

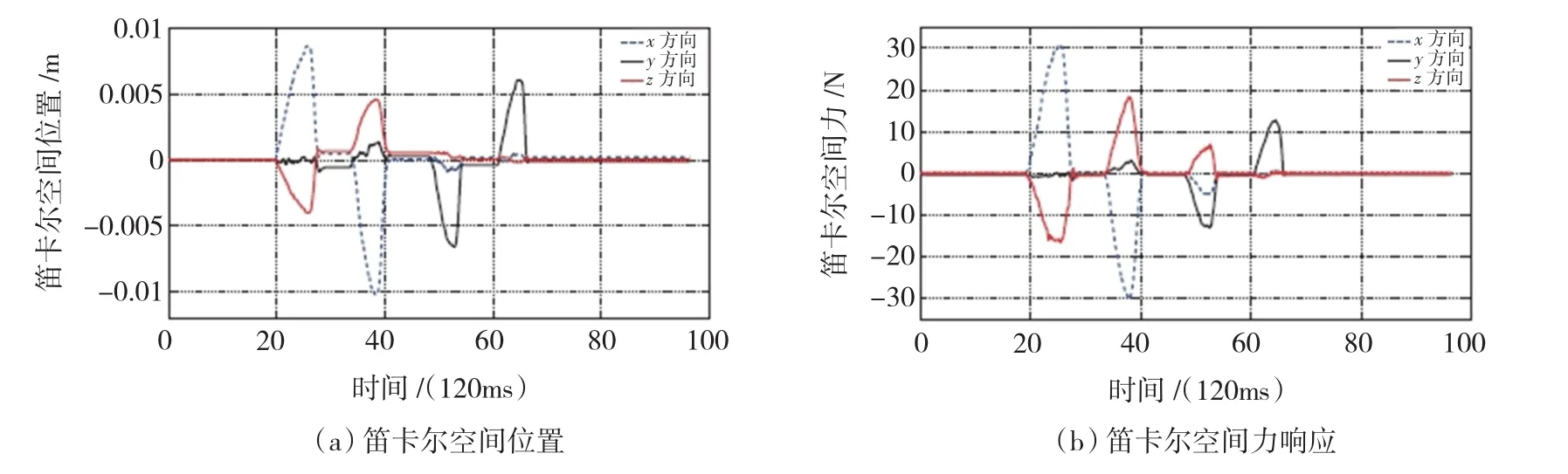
图11 机器人手指受到外力时的笛卡尔空间位置和力跟踪Fig.11 Robot finger Cartesian coordinate position and force response to external forces

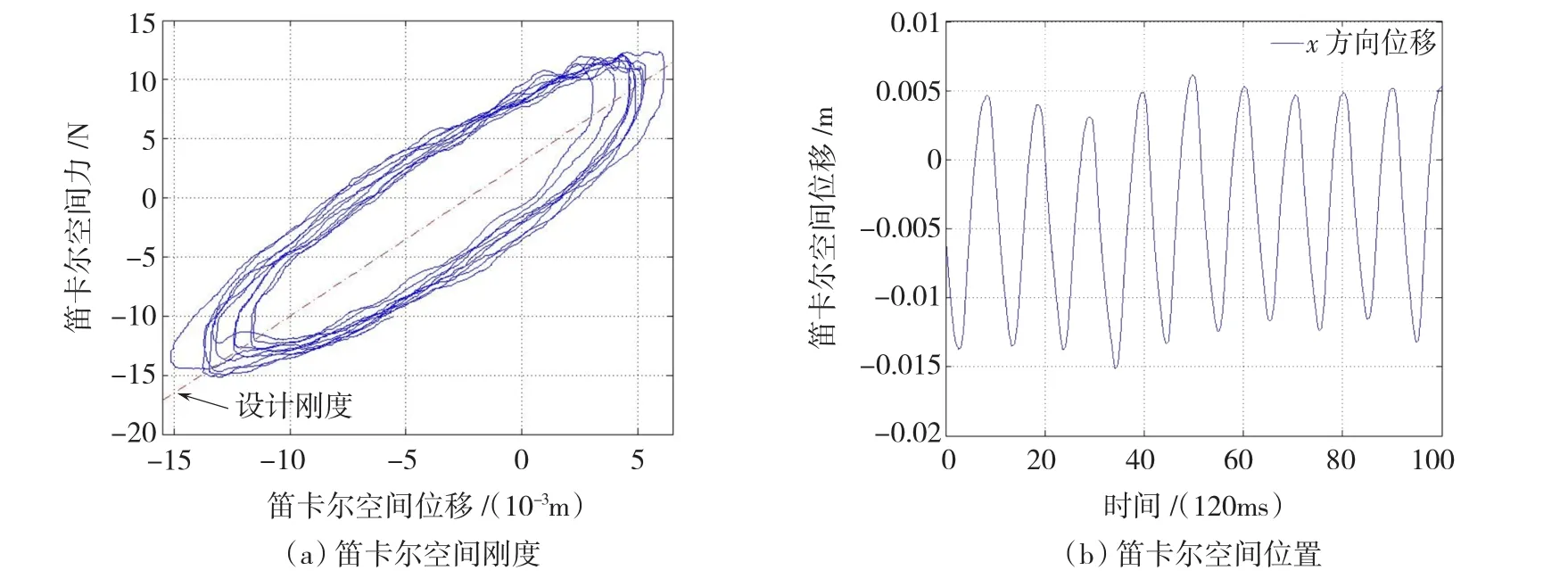
图12 x方向上位置与力的比较Fig.12 Position versus force in x-direction

5 结语

针对多指灵巧手HIT/DLR II的特点，本文提出了具有摩擦力补偿和重力补偿的柔性关节机器人自适应阻抗控制策略。基于传动系统的特殊结构形式建立了具有柔性关节和耦合关节的灵巧手动力学模型，结合该模型提出了关节空间和笛卡尔空间的阻抗控制方法。针对灵巧手各个关节重力无法确切获得的特点，提出了基于最小二乘法的实际优化方法，并通过迭代的方式采用电机端位置完成关节端重力补偿。针对灵巧手关节摩擦力的非线性问题，提出了一种基于扩展卡尔曼滤波器的摩擦力观测器，实现了对摩擦力的自适应补偿，从而完成灵巧手的自适应阻抗控制。实验结果表明，柔性关节的重力补偿及摩擦力补偿有效地提高了灵巧手阻抗控制策略的有效性。为灵巧手空间阻抗控制的进一步研究奠定了基础。在下一步的研究中，将着眼多指灵巧手的空间协调阻抗控制，以及面向抓取的自适应阻抗控制，以进一步提高仿人灵巧手的智能化和应用领域。

［1］ JACOBSEN S C，WOOD J E，KNUTTI D F.The UTAH/MIT dexterous hand:work in progress［J］.The International Journal on Robotics Research，1984，3(4):20-30.

［2］ LOVCHIK C S，DIFTLER M A.The Robonaut hand:a dexterous robot hand for space［C］//Proceedings of IEEE International Conference on Robotics and Automation，May 10-15，1999，Detroit，USA.1999，2:907-912.

［3］ BUTTERFASS J，GREBENSTEIN M，LIU H G，et al.DLRHand II:next generation of a dextrous robot hand［C］//Proceedings of IEEE International Conference on Robotics and Automation，2001，May 21-26，2001，Seoul，Korea.2001:109-114.

［4］ LIU H，MEUSEL P，HIRZINGER G，et al.The modular multisensory DLR-HIT-Hand:hardware and software architecture［J］.IEEE/ASME Transactions on Mechatronics，2008，13(4):461-469.

［5］ 樊绍巍，刘伊威，金明河，等.HIT/DLR Hand II类人型五指灵巧手机构的研究［J］.哈尔滨工程大学学报.2009，30(2):171-177.

FAN Shaowei，LIU Yiwei，JIN Minghe，et al.Research on the mechanics of the HIT/DLR Hand II anthropomorphic five-finger dexterous hand［J］.Journal of Harbin Engineering University，2009，30(2):171-177.

［6］ SWEET L，GOOD M.Redefinition of the robot motion-control problem［J］.IEEE Control Systems Magazine，1985，5(3):18-25.

［7］ GOOD M，SWEET L，STROBE K.Dynamic models for control system design of integrated robot and drive systems［J］.Journal of Dynamic Systems，Measurement，and Control，1985，107(1):53-59.

［8］ SPONG M W.Modeling and control of elastic joint robots［J］.Journal of Dynamic Systems，Measurement，and Control，1987，109:310-319.

［9］ SPONG M W，KHORASANI K，KOKOTOVIC P V.An integral manifold approach to the feedback control of flexible joint robots［J］.IEEE Journal of Robotics and Automation，1987，3(4):291-300.

［10］ GE S.Adaptive controller design for flexible joint manipulators［J］.Automatica，1996，32(2):273-278.

［11］ DE LUCA A，LUCIBELLO P.A general algorithm for dynamic feedback linearization of robots with elastic joints［C］//Proceedings of IEEE International Conference on Robotics and Automation，1998，May 16-20，1998，Leuven，Belgium.1998，1:504-510.

［12］ LOZANO R，BROGLIATO B.Adaptive control of robot manipulators with flexible joints［J］.IEEE Transactions on Automatic Control，1992，37(2):174-181.

［13］ ALBU-SCHÄER A，HIRZINGER G.A globally stable state feedback controller for flexible joint robots［J］.Advanced Robotics，2001，15(8):799-814.

［14］ ALBU-SCHÄER A，OTT C，HIRZINGER G..A passivity based Cartesian impedance controller for flexible joint robots-Part II:full state feedback，impedance design and experiments［C］//Proceedings of IEEE International Conference on Robotics and Automation，2004，April 26-May 1，2004，New Orleans，USA.2004，3:2666-2672.

［15］ ALBU-SCHÄER A，OTT C，HIRZINGER G.A unified passivity-based control framework for position/torque and impedance control of flexible joint robots［J］.The International Journal of Robotics Research，2007，26(1):5-21.

［16］ OTT C，ALBU-SCHÄER A，KUGI A，et al.On the passivitybased impedance control of flexible Joint robots［J］.IEEE Transactions on Robotics，2008，24(2):416-429.

［17］ TAKAHASHI T，TSUBOI T，KISHIDA T，et al.Adaptive grasping by multi fingered hand with tactile sensor based on robust force and position control［C］//Proceedings of IEEE International Conference on Robotics and Automation，2008，May 19-23，2008，Pasadena，USA.2008:264-271.

［18］ LE TIEN L，ALBU-SCHÄER A，DE LUCA A，et al.Friction observer and compensation for control of robots with joint torque measurement［C］//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems，2008，September 22-26，2008，Nice，France.2008:3789-3795.

［19］ BIAGIOTTI L，LIU H，HIRZINGER G，et al.Cartesian impedance control for dexterous manipulation［C］//Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems，October 27-31，2003，Las Vegas，USA.2003，3:3270-3275.

［20］ TOMEI P，A simple PD controller for robots with elastic joints［J］.IEEE Transactions on Automatic Control，1991，36(10):1208-1213.

［21］ ZOLLO L，SICILIANO B，DE LUCA A，et al.Compliance control for an anthropomorphic robot with elastic joints:theory and experiments［J］.Journal of Dynamic System，Measurement and Control，2005，127(3):321-328.

［22］ GELB A.Applied Optimal Estimation［M］.Boston:MIT Press，2002.

［23］ BROWN R G，HWANG P Y C.Introduction to Random Signals and Applied Kalman Filtering［M］. New York:Wiley Press，1992.