基于粗糙集和ANN的模拟电路故障诊断研究

田 珍，刘学会

（郑州职业技术学院 软件工程系，郑州 450121）

0 引言

随着集成电路的发展，数字和模拟器件通常被继承在单个芯片上。目前，模拟电路已被广泛地应用于军工、通信、仪表仪器和自动控制等领域。虽然模拟电路通常只占芯片面积的50%，但其发生故障的成本却占芯片总成本的95%[1]。

由于模拟电路具有原件参数离散型、可测电压节点数少、非线性和时间电压的连续性等特征，使其较数字电路的故障诊断发展要复杂和缓慢。

传统的对模拟电路进行故障诊断的方法主要是故障字典法，其具有所需测试点少和适合在线诊断的特点，但其需要先验知识且存储容量需求量大，因此不适合大规模电路故障诊断的需要[2]。

随着人工智能的发展，出现了不少采用人工智能方法实现对模拟电路进行故障诊断的研究[3～5]。 人 工 神 经 网 络 (Artif i cial Neural Network，ANN)是由大量神经元组成的庞大网络，能实现复杂信息的存储和处理。BP神经网络[3]是一种多层前馈型的人工神经网络模型， 其神经元通常采用S型函数，使其可以实现输入和输出之间的任意非线性映射，非常适合通常难以建立数学模型的故障诊断问题，但由于故障征兆的维数往往很大，使得BP神经网络的输入维数多，训练时间长，限制了其进一步的发展。

为了实现对模拟电路进行故障诊断，文中提出了一种基于粗糙集和BP神经网络的故障诊断方法。

1 粗糙集

粗糙集(Rough Set, RS)是波兰科学院Z.Pawlak教授提出的一种数学分析和推理模型，它基于集合分类理论，从数据本身出发通过对数据的分析处理，去除冗余属性从而找到隐藏在数据中的内在规律。目前，已经在机器学习、知识发现、模式识别等领域获得广泛应用。

1.1 信息系统

定义1：信息系统S可以定义为四元组：S =＜U,R,V, f ＞，其中，U={x1, x2,…, xn} 为对象的非空有限集合，R=CD为属性集，其中C为条件属性集，D为决策属性集，且满足为属性r的值域；f (U×R)→V即为论域对象对应的属性的到属性值的映射。

1.2 不可分辨关系

定义2：对于信息系统S =＜U,R,V, f ＞，对于任意属性子集A∈R，可以定义A上的不可分辨关系IND(A)，其中IND(A)的定义如式(1)所示：

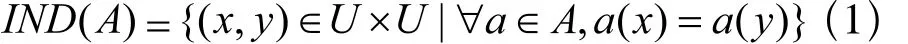
1.3 属性简约

定义3：对于信息系统S =＜U,R,V, f ＞，R=CD为属性集，其中C为条件属性集，D为决策属性集，存在 的子集A，AC，对于属性t∈A，若满足式(2):

则称t在A中是不必要的，否则称其是必要的。在公式(2)中，Ind表示满足A的等价关系的交，如果对于任意t∈A都是必要的，则称A是C的一个简约。

C的所有简约的集合记作RED(C)， 的所有简约的交集称为核CORE(C)，如式(3)所示：

2 基于粗糙集和BPNN的电路故障诊断

2.1 故障诊断模型

为了克服BP神经网络在样本数据多、维数大的情况下的训练时间过长，收敛速度过慢的问题。首先采用粗糙集对样本数据进行属性简约，然后将经过属性简约的样本数据置入到BP神经网络模型中进行训练，当BP神经网络模型的各神经元权值、阀值均已训练好后，再用训练好的BP神经网络模型进行故障诊断，其故障诊断模型如图1所示：

图1 文中故障诊断模型

2.2 粗糙集属性简约方法

定义4：基于属性出现频率的差别矩阵算法

输入：信息系统S=＜U, R,V, f ＞；

输出：简化的决策表S'=＜U', R',V, f ＞；

步骤1：初始化核属性集合CORE和简约条件属性集合RED；

步骤2：计算样本数据对应的可辨识矩阵M，将M中的单属性加入到核属性集合CORE中；

步骤3：令RED=CORE；

步骤4：删除可辨识矩阵M中包含CORE的所有项，并计算剩余的非空属性值出现的频率；

步骤5：选择M中出现频率最高的属性a，并将其加入到RED中，并从M中删除包含a的项；

步骤6：重复步骤5，直到M为空为止；

步骤8：重复步骤7，直到RED中的非核属性被遍历完为止，此时算法结束，输出最终简约条件集RED。

2.3 BP神经网络故障诊断模型

文中采用的BP神经网络故障诊断模型采用三层典型网络，可分为输入层、隐层和输出层，如图2所示。

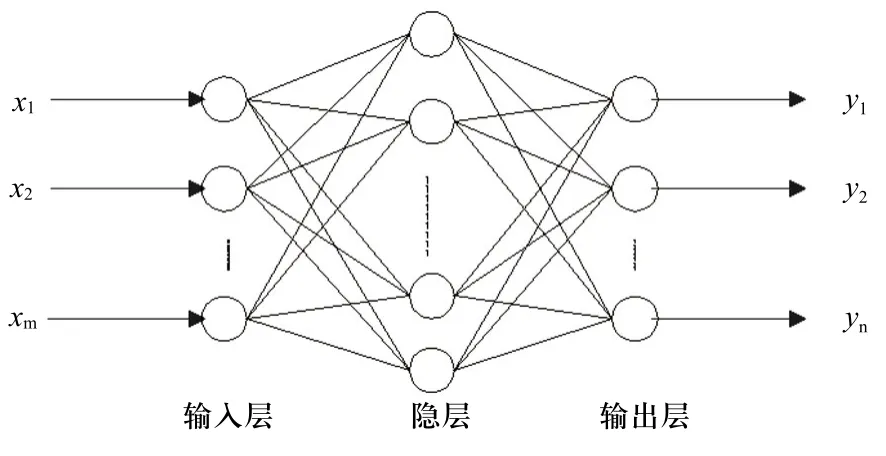
图2 三层BP神经网络模型

定义5：属性简约的BP神经网络故障诊断算法

步骤1：首先通过定义4所示的基于属性出现频率的差别矩阵算法实现对样本数据进行属性简约，得到简约的属性集，其维数为L；

步骤2：当训练数据维数L确定后，则输入层神经元的个数为L；

步骤3：根据故障种类来确定输出神经元个数M；

步骤4：通过经验公式(4)确定隐层神经元个数：

在式(4)中，q为1到10之间的一个随机数。

步骤5：将步骤1得到的简约后的样本数据置入到图2所示的BP神经网模型进行训练，并根据公式(5)计算输出端误差：

式(5)中，Yj表示第j个输出神经元的期望输出，表示第j个输出神经元的实际输出；

步骤6：根据输出层的误差，按照误差反向传播算法对各神经元权值、阀值等进行调整；

步骤7: 当误差满足目标值时，训练结束，此时的BP神经网络模型即为故障诊断模型；

步骤8：输入测试数据，采用训练好的BP神经网络进行故障诊断，得到故障诊断结果。

3 模拟电路故障诊断试验

为了对文中方法进行验证，采用图3所示的模拟放大电路来进行故障诊断试验,各参数如下:输入信号源为幅值Vm=1000mV和频率f =1000Hz的正弦信号，R1=400Ω，R2=1000Ω，R3=800Ω，R4=R7=R8=2000Ω，R5=600Ω，R6=900Ω， 电 容C1=C2=C3=C4=20uF。

图3 某模拟放大电路

在图3中，选择电路图中out1、out2、out3、out4和out5处的测量电压为特征向量，分别部分电容、三极管和电阻进行故障诊断，得到1组样本数据如表1所示。

表 1 测点电压值对应的故障状态

首先对表1中的数据进行离散化处理，再通过粗糙集进行属性简约得到的特征向量为out1、out2和out4，如表2所示。

表2 离散并简约后的特征向量

从表2中可以看出，简约后的特征向量仅3个，将其作为神经网络的输入端，则输入端的神经元个数为3，故障种类一共为7种，采用二进制编码所需要的输出端神经元为4个，则根据公式(4)可以将隐层神经元定为5个，神经网络为3-5-4结构。

采用表2的简约样本数据对网络进行训练，并采用8组测试数据进行故障诊断，得到的故障诊断准确率为98.34%。

采用文中基于粗糙集的BP神经网络方法与传统的BP神经网络方法进行比较，得到的训练曲线如图4所示，从中可以看出：BP神经网络和文中方法在迭代400次时，BP网络的误差为0.01，而文中方法的误差已收敛到0.0001，这证明文中方法不仅使得BP神经网络训练速度加快，而且提高了诊断精度。

图4 文中方法与BP神经网络误差对比

4 结论

本文提出了一种能对模拟电路进行故障诊断的方法，能快速并精确地对模拟电路中的各种故障进行有效诊断。首先对样本数据采用可辨识矩阵进行属性简约，然后将简约后的特征向量置入

BP网络输入端进行训练，将训练后的神经网络作为故障诊断推理模型。实验表明经过粗糙集简约后的BP神经网络能正确地实现故障诊断，且与未进行简约的BP神经网络故障模型相比，误差大为减少，具有重要的意义。

[1] 叶笠, 王厚军, 田书林, 等.容差模拟电路软故障诊断的一种方法[J].电工技术学报, 2011, 26(5): 119-125.

[2] 雷邵充, 邵志标, 梁峰.超大规模集成电路测试[M].北京: 电子工业出版社, 2008: 231-250.

[3] 宋丽伟, 彭敏放, 田成来, 沈美娥.基于PSO-RBF神经网络的模拟电路诊断[J].计算机应用研究, 2012, 29(1): 72-74.

[4] 赵光权, 彭喜元, 马勋亮.基于微分进化神经网络的模拟电路故障诊断[J].测控技术学报, 2012, 26(1): 88-92.

[5] 邓 森, 杨军锋, 郭明威, 郭创, 基于模糊SVM和虚拟仪器的模拟电路故障诊断研究[J].计算机测量与控制.2011.19(4): 762-765.

[6] Jian-Da Wu,Cheng-Kai Huang, Yo-Wei Chang.Fault diagnosis for internal combustion engines using intake manifold pressure and artif i cial neural network [J].Expert Systems with Applications，2010,37,949-958.

[7] Pawlak Z Rough sets[ J ].International Journal of Computer and Information Sciences, 1982 (11) : 341-356.