高通过性变形轮行走机构的模态分析
王东亮,郭晓燕
(中国北方车辆研究所,北京 100072)
无人地面车辆及其相关技术是当今世界科学技术发展最活跃的领域之一,最早的研究是出于军事领域的需要,目前在军事、民用领域的研究都得到了大力发展[1-2].国外研制的无人地面车辆为增强其地形适应能力,改变了传统的单一的轮式或履带式行走机构,而是采用新型的高通过性行走机构及相关技术.而目前国内对无人地面车辆的研究还只限于少数几种类型,尤其是对高通过性行走机构及其技术的研究比较少,与发达国家相比还有相当的距离.因此,开展高通过性行走机构及其技术的研究,对于加速我国无人地面车辆的发展,提高无人地面车辆的地形适应能力,具有极其重要的意义.
为提高行走机构的通过能力,尤其是在松软路面上的通过能力,车辆多采用松软路面轮胎或压力轮胎系统[3].与普通轮胎相比,松软路面轮胎或压力轮胎系统能改变车轮的接地面积,但改变量有限,且压力轮胎系统结构复杂,成本较高.变形轮行走机构利用变形轮圈的变形来改变接地面积,它兼有轮式行走机构和履带式行走机构的优点,既有较高的行驶速度又有良好的通过能力.
1 机构工作原理及特点
1.1 机构工作原理
变形轮行走机构的原理示意图如图1所示,包括变形轮圈1、驱动轮2、限位轮3、限位轮4和导向轮5.变形轮圈由弹性材料 (如橡胶、金属弹性材料等)制成,其弹性特性由使用条件和承受载荷而定.变形轮圈1的内表面有轮齿,通过驱动轮2与导向轮5,以啮合的方式行驶.驱动轮2和导向轮5对称地分布在变形轮圈1圆心垂线两边,其夹角根据实际尺寸而定,但最大不超过180°.为保证变形轮圈1的正常行驶,在驱动轮2和导向轮5相应处安装限位轮3和限位轮4.
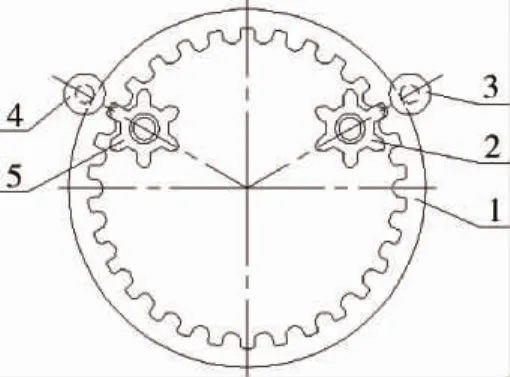
图1 机构组成原理图
机构受载时,如图2所示,在载荷作用下变形轮圈发生变形,由圆形变为近似椭圆形,且载荷越大,变形也越大,从而改变接地面积,减小单位压力,提高车辆的通过能力.

图2 受载变形图
1.2 机构特点
轮式行走机构由于轮胎的变形量有限,在松软路面上行驶时,容易发生沉陷和打滑,而变形轮行走机构通过变形轮圈的变形获得较大的接地面积,从而提高在松软路面上的通过能力.履带式行走机构由于自身的“链式”结构,不适合高速运动的情况,而变形轮行走机构克服了这一缺陷,运动速度相对较高.它充分结合了两种行走机构的优点,既有较高的行驶速度又有良好的通过能力,其地形适应能力大大增强.
变形轮圈具有较好的弹性,相当于悬架中的弹性元件,导向轮和限位轮对变形轮圈起导向和支撑作用,相当于悬架中的导向元件,故机构本身具有悬架的作用,车辆无需另装悬架,这是该机构的另一亮点.
2 变形轮圈的模态分析及系统阻尼匹配
2.1 变形轮圈的模态分析
模态对于结构刚度及系统振动特性影响较大.分析系统振动特性,有必要对变形轮圈的模态进行分析.实际的机械结构系统可以看成多自由度的振动系统,具有多个固有频率,每个固有频率对应一个振型.这种结构所具有的基本振动特性称为结构的模态.模态分析的目的在于确定结构的振动特性,找出结构的共振频率和有害振型,以指导系统结构或部件的设计[4].对于机械系统而言,低阶模态对系统的振动影响较大,远离振源频带的高阶模态对系统的实际振动影响较小.因此,这里分析前10阶模态.图3、图4为典型模态振型,表1为前10阶模态频率.

图3 1阶模态振型

图4 10阶模态振型

表1 前10阶固有频率统计表 Hz
文中设计的变形轮圈材料为橡胶,分度圆半径为96 mm,齿根圆半径为102 mm,齿顶圆半径为94 mm,齿数为36.对于该变形轮圈而言,1阶、2阶、3阶、6阶、8阶、9阶模态主要为摆动,4阶、7阶、10阶模态主要为扭振.变形轮圈的1阶模态频率距离车身的固有频率较远,因此,变形轮圈的振动不会引起车身共振.对于路面激励,若研究30 Hz以内的频段,变形轮圈的前4阶模态频率都在此范围内.说明此频段的路面激励可以引起变形轮圈的共振,但可通过添加阻尼元件来改善.
2.2 阻尼匹配
变形轮行走机构的主要特点之一就是机构本身具有悬架的功能,变形轮圈兼起弹性元件的作用.由汽车理论及振动理论可知,减振器的阻尼系数是影响车辆特性尤其是平顺性的主要参数之一.减振器的阻尼系数越大,振动消除越快,但却使弹性组件的作用不能充分发挥,同时,过大的阻尼使减振器本身温度过高,从而导致密封件损坏;而减振器阻尼系数过低,振动消除的太慢,行驶平顺性变坏[5].因此,悬架阻尼与刚度匹配是否合适对车辆特性有很大影响,有必要对行走机构进行阻尼匹配分析.另外,上文已分析变形轮圈的振动模态,路面激励能引起系统共振,为消除或改善这种共振,也需对行走机构进行阻尼匹配分析.
图5是单质量系统模型,它由簧上质量m和弹簧刚度K、减振器阻尼系数C的悬架组成.q是输入的路面不平度函数.

图5 单质量系统模型
簧上质量垂直位移坐标z的原点取在静力平衡位置,根据牛顿第二定律,得到系统的运动微分方程为
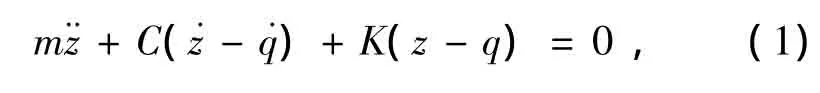
系统的固有频率为

阻尼比为
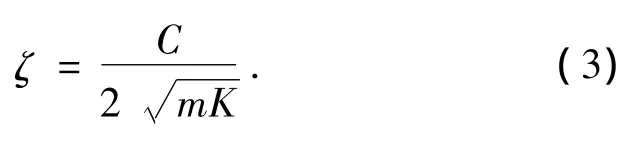
阻尼比对车辆的平顺性影响很大,车辆工程中阻尼比一般取0.2~0.4.
阻尼比取0.2,由公式 (3)可得
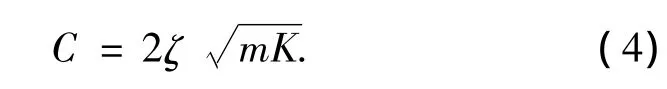
文中设计的行走机构,簧上质量为1.25 kg,平衡位置时的变形量h为17.3 mm,则该处刚度值由下式计算.

将式 (5)代入式 (2)即可得固有频率f0=3.8 Hz.此时匹配的阻尼可由式 (4)求得C=12.02 N/m·s-1.
3 结论
在阐述新型的变形轮行走机构工作原理与特点基础之上,重点进行了模态分析.结果表明:变形轮圈的模态频率距离车身的固有频率较远,变形轮圈的振动不会引起车身共振;路面激励可以引起变形轮圈的共振,通过对系统进行阻尼匹配,求得系统的阻尼,添加具有此阻尼的阻尼元件可减弱因路面激励引起的振动.
需要说明的是,文章新型行走机构的探讨与尝试,有很多方面需要进一步深入研究.
[1]徐国华,谭 民.移动机器人的发展及其趋势[J].机器人技术与应用,2001,(3):6-14.
[2]吴邵斌,陈慧岩.军用地面无人车辆的发展 [J].机器人技术与应用,2001,(3):49-54.
[3]状继德.汽车地面力学[M].北京:机械工业出版社,1980.
[4]张克健.车辆地面力学[M].北京:国防工业出版社,2002.
[4]李德葆,陆秋海.试验模态分析及其应用 [M].北京:科学出版社,2001.
[5]余志生.汽车理论[M].4版.北京:机械工业出版社,2008.
- 车辆与动力技术的其它文章
- 特种车辆扭矩测试仪的研制
- 车辆多体动力学仿真中的路面模型构造方法的研究

