基于基础坐标概念的逐点比较法圆弧插补原理及其应用

赵庆志，席港港

ZHAO Qing-zhi, XI Gang-gang

0 引言

经济型数控机床能够满足常规加工需要、价格较低、操作简单、性价比较高，占有比较大的市场，该类数控机床常采用逐点比较法圆弧插补方法。

1 传统的逐点比较法圆弧插补原理存在的问题及其改进

传统的逐点比较法圆弧插补原理分为以下四个步骤：偏差判别、坐标进给、新点偏差计算和终点判别。在坐标进给时并没有考虑进给后插补误差的大小而决定进给坐标，致使插补误差较大，这种插补方法使得刀具每次在X或Y坐标进给一个脉冲当量，而不能使得X、Y两坐标同时联合进给。图1所示为插补逆圆弧时产生了较大的插补误差。事实上当圆弧切线趋向于45°斜线时若能X、Y两坐标同时进给一步，插补误差就大大减小[1～7]；在图1所示的起点A若进给+Y也能大大减小插补误差，本文在前人研究的基础上，引进基础坐标的概念，研究出了逐点比较法圆弧插补新原理，简化了插补过程，大大减小了插补误差，用该方法开发数控系统控制程序很方便。

新逐点比较法圆弧插补步骤改为：先确定基础坐标[8]，插补四个步骤改为：两种进给方案的新点偏差计算、偏差大小比较、基础坐标或双坐标进给、终点判别。即先分别计算出F、Fxy两种进给方案新点的偏差值，然后比较两者大小，再决定基础坐标进给还是两坐标联合进给。令F代表基础坐标进给一步后的插补偏差，Fxy代表两坐标X、Y联合进给后的插补偏差。

1.1 改进后逐点比较法圆弧插补原理推导

如图1所示，第一象限逆圆弧AB由A点向B点加工，插补过程动点坐标为（Xi，Yi），则传统的逐点比较法圆弧插补原理偏差判别函数为[8]：

起点坐标A(X0,Y0)=A(5,0)。当X0＞Y0时，为保持偏差F趋于0，Yi增大的速度就比Xi快；当Y0＞X0时，为保持偏差F趋于0，Xi增大的速度就比Yi快；所以分如下三种情况分析进给新点的偏差计算和坐标进给：

1）当X0＞Y0时，每次进给都进给+Y基础坐标，只是考虑在什么条件下+Y、-X两坐标联合进给，不再考虑单独进给-X坐标。

进给+Y坐标一步新点的坐标为（Xi，Yi+1）=( Xi，Yi+1),带入（1）式得新点的偏差：

在此对偏差F省去下标，默认公式右边的F是上次插补偏差，以下同，式（2）记为：

联合进给-X、+Y一步新点的坐标为（Xi+1，Yi+1）=(Xi-1，Yi+1),带入（1）式得新点的偏差为：

图1 传统逐点比较法圆弧插补轨迹

(3)、(4)两公式即表1中第3组公式，显然，当|F|＜|Fxy|时，只进给基础坐标+Y，Fxy=F；当|F|≥|Fxy|时，联合坐标进给-X、+Y，F=Fxy；即取插补偏差小的进给坐标进给。

2）当X0＜Y0时，每次进给都进给-X基础坐标，只是考虑在什么条件下-X、+Y两坐标联合进给。不再考虑单独进给+Y坐标。-X坐标进给一步的插补偏差公式为：

联合进给-X、+Y一步新点的偏差计算公式为（3）式。

显然，当|F|＜|Fxy|时，只进给基础坐标-X坐标一步，Fxy=F；当|F|≥|Fxy|时，联合进给两坐标-X、+Y，F=Fxy；即取插补偏差小的进给坐标进给。

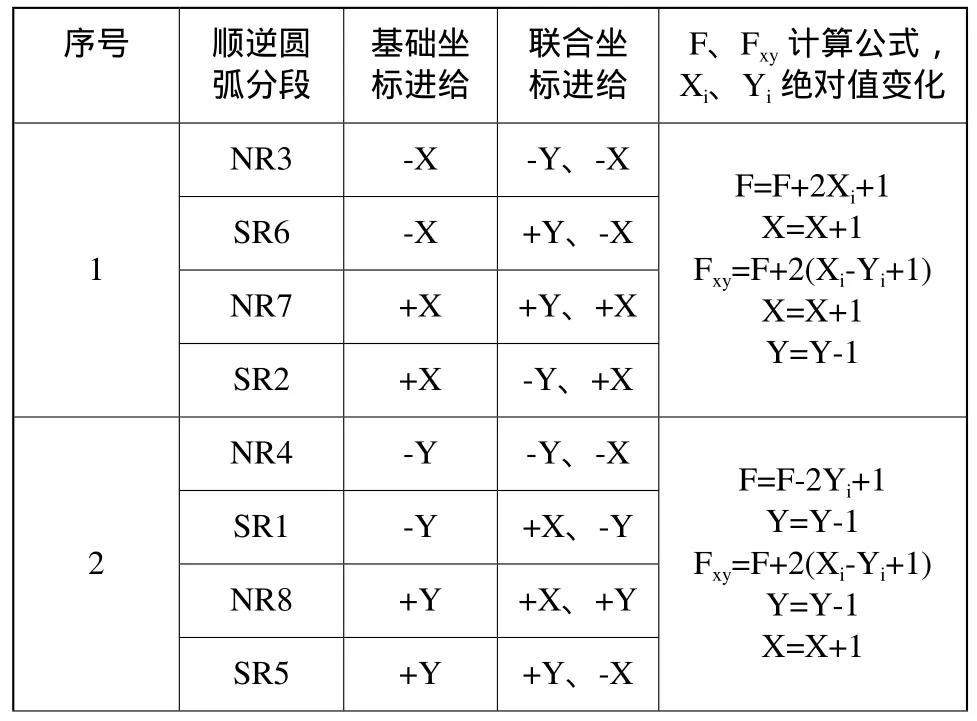
表1 顺逆时针各段圆弧插补公式

续表

3）插补过程中，动点Xi、Yi的大小发生变化时，基础坐标调换，则插补公式相应调换。

1.2 改进后的各象限逐点比较法圆弧插补公式与坐标进给

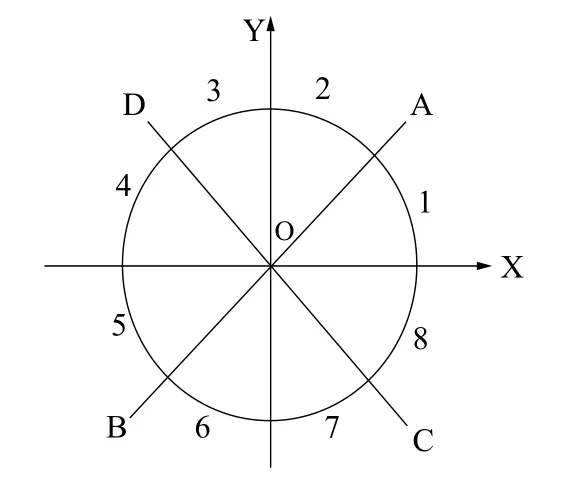
图2 四个象限分成8个基础坐标区域圆弧

图3 基于基础坐标概念的逐点比较法圆弧插补框图

图2所示的四个象限被两条过坐标原点交叉的45°直线分为8个区域，不管逆时针圆弧还是顺时针圆弧，1、4、5、8段分别记为NR1、NR4、NR5、NR8段圆弧的基础坐标为Y坐标；不管逆时针圆弧还是顺时针圆弧，2、3、6、7段圆弧的基础坐标为X坐标；推导归纳出顺逆时针各8段圆弧插补公式如表1所示，基于基础坐标的逐点比较法圆弧插补原理如图3所示，n=|Xe-X0|+|Ye-Y0|是对一个象限的圆弧计算的，当圆弧在几个象限时要分别计算相加得n。

1.3 基于基础坐标概念的各象限逐点比较法圆弧插补相关问题

1.3.1 插补过程中基础坐标的转换

插补过程中插补坐标Xi、Yi不断变化，就会出现基础坐标变换，这时要按表1相应变换插补公式。如图2所示第一象限逆时针圆弧被45°直线分成1、2两段，NR1开始时X0＞Y0基础坐标为+Y，用第3组插补公式，当插补动点Xi≤Yi时按表1圆弧变为NR2，基础坐标变为-X，改为用第4组插补公式，图4是用新插补方法对图1进行插补轨迹。

1.3.2 插补过程中的过象限处理

过象限的标志是动点坐标之一为0，对图2所示1、2、3、4……逆圆弧,当Xi=0时由第一象限过到第二象限；当Yi=0时由第二象限过到第三象限等等，顺圆弧也以此类推，过象限时按表1插补公式变换。

图4 基于基础坐标概念的逐点比较法圆弧插补轨迹

2 基于基础坐标概念的逐点比较法圆弧插补案例

图4所示为用基于基础坐标概念的逐点比较法圆弧插补原理对图1所示圆弧进行插补的轨迹图，按照图3所示框图插补进行如下：

n=(|0-5|+|5-0|)+(|-3-0|+|4-5|)=14,在自A点向B点插补时，因为X0＞Y0，所以按表1所示NR1的信息进行插补，整个插补过程见表2，经历了基础坐标变化、插补公式变换、过象限处理等问题处理，插补轨迹如图4所示，图4比图1的插补误差明显减小了。

表2 图4所示基于基础坐标概念的逆圆弧插补过程

3 基于基础坐标概念的逐点比较法圆弧插补原理的应用特点

本文介绍的基于基础坐标概念的逐点比较法圆弧插补原理有如下五个特点。

1） 将传统的逐点比较法圆弧插补公式提炼成表1所示4套公式，插补思路更加清晰，插补信息一目了然。

2） 图3所述基于基础坐标概念的逐点比较法圆弧插补框图符合结构化程序一进口两出口分支结构的特点，与有关文献研究提出的多分支结构相比，使得开发数控控制程序更加方便。

3） 该方法避免了有关文献所述方法中涉及的导数计算、有可能出现斜率无穷大、多分支判断支路多、计算麻烦等缺点。

4） 新插补方法通用性强，使得表2所示的基础坐标变换、过象限处理等数据信息自然过渡衔接，不易出错。

5）由表2看出，图4所示的14步坐标进给只用10步插补就完成了，插补速度得以提高。

4 结束语

该方法已在作者开发的数控雕刻机控制系统中得到了实际应用，效果很好。

[1] 张涛, 王晓明. 实现步进电动机双轴联动的改进逐点比较法(自然科学版)[J]. 化学工程与装备, 2011, (2): 6-7.

[2] 范希营,郭永环. 提高数控系统基准脉冲直线插补速度及精度的研究[J]. 制造技术与机床. 2010, (3): 89-91.

[3] 权秀敏, 尹显明. 一种简捷的快速圆弧插补新算法的设计与计算[J]. 机械研究与应用, 2008, (1): 77-79.

[4] 李峰. 圆弧插补的改进及软件实现[J]. 湖北汽车工业学院学报, 2004, (12): 77-79.

[5] 高有行. 对逐点比较法的改进算法[J]. 西安电子科技大学学报, 1998, (6): 299-303.

[6] 刘云. 基于统一偏差判别函数的各象限直线的逐点比较插补算法[J]. 长春师范学院学报, 2001, (6): 1-4.

[7] 马斌. 逐点比较法的改进及软件实现[J]. 渝州大学学报,2002, (2): 77-79.

[8] 王敏. 差分插补方法及其在数控线切割机中的应用(一)[J].电加工, 1981, (4): 16-22.