基于ANSYS的搅拌摩擦点焊机器人关键部件的分析与优化设计

张 松，乔凤斌，赵维刚

（上海航天设备制造总厂，上海 200245）

0 引言

搅拌摩擦焊是一种固相连接方法，自发明以来，引起了世界范围的广泛关注。该焊接方法是在压力作用下，通过待焊工件的摩擦界面及其附近温度升高，材料的变形抗力降低、塑性提高和界面氧化膜破碎，伴随着材料产生塑性流变，通过界面的分子扩散和再结晶而实现焊接的固态焊接方法[1]。搅拌摩擦点焊机器人是在搅拌摩擦焊基础上，新近研究开发的一种创新的固相焊接设备, 其焊接机理是搅拌头周围高温摩擦热和材料塑性流动相互作用的结果[2]。机械结构特性分析是设计中的重要环节，使用ANSYS有限元分析软件不仅可以进行简单的线性和静态分析，也可以进行复杂的非线性和动态分析，从而对设计方案进行参数化优化设计。

1 有限元模型的建立

对搅拌摩擦点焊机器人进行有限元分析的第一步便是如何将机械结构系统转化成由节点及元素所组成的有限元模型，该有限元模型与机械结构系统的几何外形一致。先建立实体模型，再进行网格划分，完成有限元模型的建立。搅拌摩擦点焊机器人关键承载部件为腰部、大臂及小臂，其结构较为复杂，所以通过Pro/E与ANSYS的接口（格式：X_T）将CAD模型导入到ANSYS中。

2 实体模型的简化与网格划分

从CAD到CAE的转化过程中，由于CAD三维模型具有过多的特征和细节结构，且不同软件在算法和设计上有所差异，模型中比较小的特征可能会失真，导致实体模型的有限元网格划分不易。通常对实体模型的细节进行一定的几何简化，忽略一些不必要的细节，去除一些对分析影响不大的零件及特征，以利于有限元分析[3]。立足于机器人运动特性和样机结构特性，为保证全面准确的反映部件的刚度，同时合理简化有限元模型，在不影响所要求的分析精度下，对机器人关键部件的三维模型进行适当简化，使其能符合ANSYS分析的要求，从而节省大量的分析时间，避免资源的浪费。

网格划分主要包括选取单元数据和设定网格划分的参数。机器人的腰部、大臂和小臂均为实体，用三维实体单元描述，更能反应其真实状况。

3 关键部件的模态分析

随着结构向着重载、高速和轻量化的方向发展，对机械结构进行动态设计的要求越来越迫切，结构模态分析是结构动态设计的核心，是结构强迫振动分析的基础。

多自由度系统振动时，同时有多阶模态存在，每阶振动模态可用一组模态参数来确定。模态参数表明在哪几种频率下结构会产生共振以及在各阶频率下结构的相对变形，对于改善结构动态特性具有重要的意义。模态分析过程中将对大臂、小臂和腰部模型进行简化，求出前六阶固有频率和固有振型即可[4]。经ANSYS分析计算，可得到腰部和小臂的固有频率值，结果表明这三个关键部件均具有较高的固有频率，工作中不易发生共振，其结构动力学性能良好。

4 关键部件的静力分析

由于机器人大臂、腰部和小臂三个部件在运动过程中几乎承受了全部的负载，需要进行静力分析。通过动态仿真，可得到考虑加速度情况下三个部件的边界条件和受力情况。根据机器人整个工作系统之间的约束关系，大臂、小臂和腰部的约束均为一端固定，另一端受载荷作用[5]。大臂、小臂和腰部所承受的载荷类型相似，主要有零件自身重力（输入重力加速度就可以模拟）和集中载荷（来自负载，包括装配反力和与之有装配关系的工件施加给它的弯矩和扭矩）。以机器人腰部为例，经 ANSYS分析计算，腰部的有限元分析结果分别如图1所示。

由腰部的分析结果可知，腰部的最大应力发生在腰部与大臂连接的端面上，最大应力值31.6Mpa，而铝合金的许用应力为235Mpa，显然结构合理、满足强度要求且裕度较大。最大变形量为0.12mm，发生在腰部的前端面上。

同理可对大臂、小臂进行分析计算，静力分析结果表明各关键部件最大应力都远远小于铝合金的许用应力值，裕度非常大，而且其变形量都很小[6]。

5 关键部件的优化设计

图1 腰部的应力和变形分布云图

优化设计将实际问题首先转化为最优问题，然后运用最优化原理和方法，从满足各种设计要求及限制条件的全部可行方案中，选出最优设计参数，获得最优值。通过优化设计，能够使零件的力学性能得到改善，并且获得理想的结构布局和尺寸[7]。利用ANSYS的优化模块对搅拌摩擦点焊机器人的关键承载部件进行优化设计，以在满足结构强度、刚度的条件下，质量最轻为优化原则,进一步提高机械系统的各项性能。

5.1 设计变量的选定

选取腰部的前筒壁厚d1和中间电机孔径d2为设计变量，如图2所示，其余作不变量。

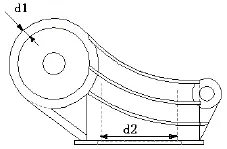
图2 腰部的设计变量

优化范围：

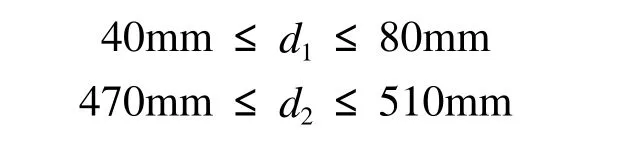
5.2 状态变量的选取

根据强度校核理论，铝合金通常以屈服的形式失效，故采用第三和第四强度理论进行校核。

σmax＜ [σ]＝ 235Mpa

腰部受载荷后的变形和小臂类似，相比大臂要小，所以现要求其最大变形量dmax的范围为：

－0.075mm≤δmax≤0.075mm

5.3 目标函数的确定

优化目标函数为：

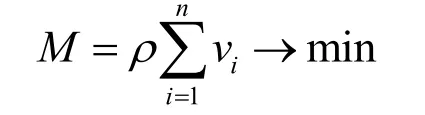
因此，确定优化数学模型为：

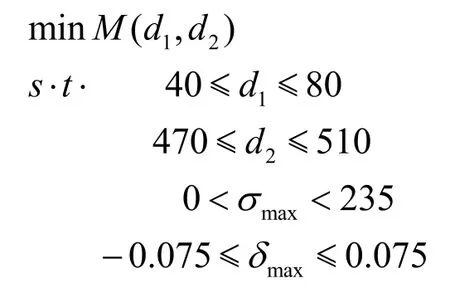
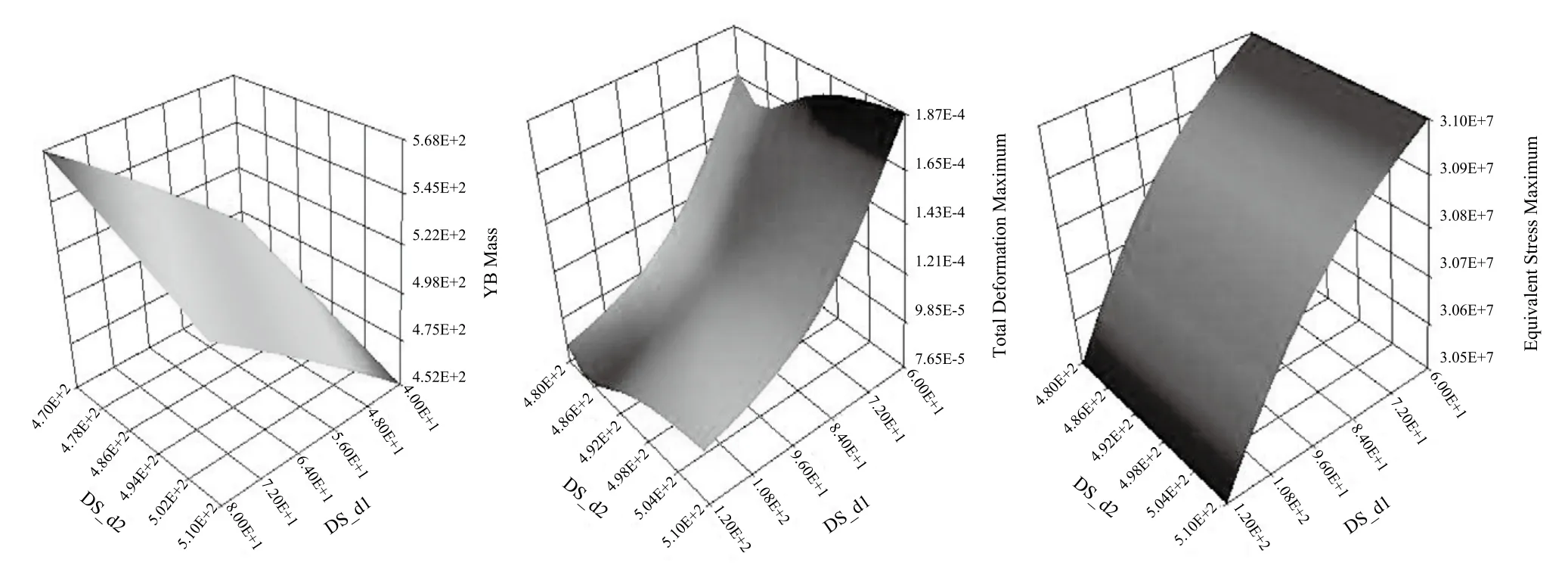
图3 腰部的质量、变形量和最大应力分别和各设计变量的关系图

5.4 腰部优化结果分析

执行ANSYS程序对腰部进行强刚度计算，经过反复改变腰部的结构参数，得到腰部的质量、变形量和最大应力相对应于设计变量的关系如图3所示。

最终优化后的应力和变形云图如图4所示。

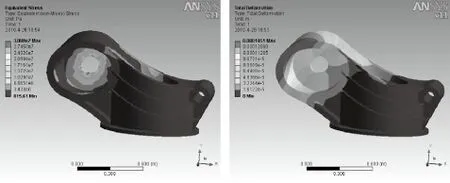
图4 优化后腰部的应力和变形云图

从优化前后腰部的设计变量、状态变量和目标函数的数据可知：最优解的最大应力和最大变形都在许用范围之内且裕度有所减少。优化后虽然第一阶固有频率值有所下降，但仍远大于机器人的工作频率，不影响其动力学性能。优化前后，腰部质量分别为573.62kg和539.87kg，优化后比其优化前的质量减轻了约5.9%，优化效果不佳。

图5 加肋板支撑后腰部的应力和变形云图

从腰部受力后的变形云图看出，腰部的变形主要发生在腰部前筒面，且偏向一边。这是由于腰部前筒一端需安装电机，该端结构上近似盲孔，另一端则是通孔。近似盲孔端可以看作是有肋板支撑着圆筒，所以该端变形较小，而另一端通孔处由于没有类似的肋板支撑结构，所以变形较大。因此，在优化后的模型通孔一端也加上类似结构，经过ANSYS计算后其应力和变形云图如图5所示。

从图5中可以看出，虽然最大应力没什么变化，但是腰部的最大变形从0.13mm减小到了0.09mm。因此，在通孔那端加上圆环肋板，进一步优化。设计变量除了腰部的前筒壁厚d1和中间电机孔d2之外，还包括肋板的厚度d3和肋板上的圆孔直径d4。

腰部的优化数学模型变为：

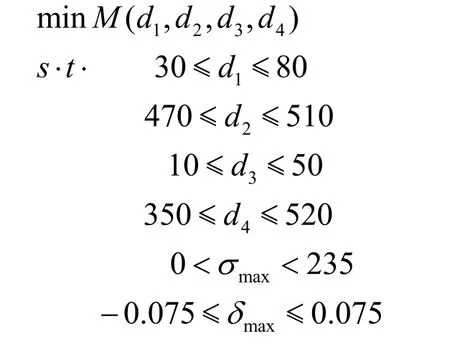
执行ANSYS程序对腰部进行进一步的优化计算，得到腰部的质量、变形量和最大应力相对应于设计变量的关系。最终加肋板支撑模型优化后的应力和变形云图如图6所示。

图6 加肋板支撑模型优化后腰部的应力和变形云图

从第二次优化前后腰部的设计变量、状态变量和目标函数值可知，腰部加了肋板支撑后，在同等的约束条件下，腰部前筒壁厚可进一步减小，从上次优化后的66.69mm减小到31.885mm，质量从上次优化后的539.87kg减小到462.95kg，此次优化后的质量比其不加肋板时优化的质量减小了约14.3%，比最初始的质量减小了19%，且一阶固有频率从313.98Hz增加到350.86Hz，动力学性能进一步提高，优化效果良好[8]。

6 结论

运用ANSYS软件对搅拌摩擦点焊机器人的关键承载部件进行了模态分析和静力分析，得到了各部件的固有频率、振型及应力、变形分布等情况，并以此为理论依据进行了优化设计，最终在满足强度、刚度和最大变形量要求的基础上，使结构性能进一步提高，对搅拌摩擦点焊机器人设备的研制具有重要意义。

[1] 秦红珊, 杨新歧.搅拌摩擦点焊技术及在汽车工业应用前景[J].汽车技术, 2006(1): 1-4.

[2] 赵衍华, 张丽娜, 刘景铎, 杜岩锋, 王国庆.搅拌摩擦点焊技术简介[J].航天制造技术, 2009(2)4: 1-5.

[3] 龚曙光.ANSYS工程应用实例解析[M].北京: 机械工业出版社, 2003.

[4] 赵恒华, 高兴军.ANSYS软件及其使用[J].制造业自动化.2004(5)20-23.

[5] 邵蕴秋.ANSYS 8.0有限元分析实例导航[M].北京: 中国铁道出版社, 2004.

[6] 侯剑平, 赵万争, 李正刚.动力学分析及有限元法在机器人本体设计中的应用[J].机器人.2005, 22(7): 12-15.

[7] 赵伟, 殷国富, 陈航, 周晓军.基于SolidWorks和ANSYS的机器人手臂性能分析与优化设计[J].机械.2009, 36(12):48-50.

[8] 谢志江, 孙玉, 李诚, 倪卫.基于ANSYS Workbench的搬运机械手结构优化设计[J].机械与电子.2010(1): 65-67.