基于Hopfield 神经网络的谐波电流提取方法

孙改平，杨尔滨，王俊宇

(上海电力学院电力与自动化工程学院，上海 200090)

近年来，由于非线性负载(整流器、变频器等)的大量使用，使得电能质量问题变得日益严重，其中谐波污染对供用电设备和电网的经济运行造成了严重影响.谐波会引起诸如设备过热、损耗增加、电流过大、电容击穿、保护装置误动作及测量仪表不准确等危害［1］，必须予以抑制.目前，谐波已成为污染电力系统的主要因素之一，谐波含量也成为衡量电能质量的重要指标之一［1，2］.

为了准确、实时地检测出电网中瞬时变化的谐波，国内外专家提出了多种检测方法.现有的谐波检测方法按照原理可分为模拟滤波器法、基于Fryze传统功率定义的方法、基于瞬时无功功率理论的方法、基于傅里叶变换的方法、基于小波分析的方法等.上述方法的计算量较大，检测时间较长并且对故障类型有一定的要求［3-5］.

人工神经元网络(Artificial Neutral Networks，ANN)已被广泛应用于模式识别、信号处理、智能控制等领域.近年来，电力系统的谐波治理领域也出现了多种基于神经网络的检测算法，如需要基于多层前馈的自适应网络，利用加窗插值算法的网络和基于三角函数的神经网络算法等.这些方法具有较高的准确性，同时也避免了对于给定补偿电流的复杂计算，具有广泛的适应性.

本文利用一种基于连续型的Hopfield神经网络(Continued Hopfield Neural Network，CHNN)进行谐波电流的提取，并通过仿真对其进行验证.

1 CHNN模型

1.1 CHNN自适应网络

连续型Hopfield自适应网络(CHNN)是一种循环神经网络，从输出到输入有反馈连接，在输入的激励下会不断产生状态变化.连续型Hopfield神经网络的模型结构如图1所示.

图1 连续Hopfield神经网络模型

每一个神经元均具有连续时间变化的输出值，采用具有饱和非线性的运算放大器来模拟神经元的S型单调输入输出关系，即vi=fi(ui).对于一个N节点的CHNN模型来说，其神经元状态变量的动态方程可以用下述非线性微分方程组来进行描述:

根据Hopfield理论，系统在运动过程中其内部储存的能量函数随着时间的推移而逐渐减少.当达到平衡状态时，系统的能量耗尽或耗至最少，并将在此平衡状态处渐近稳定，即当dE/dt=0时，有 dvi/dt=0，其中 vi(i=1，2，…，N)为网络的状态.其能量函数［6］定义为:

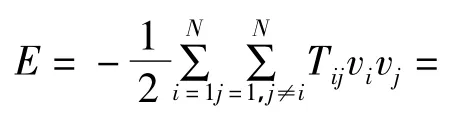
若对反馈网络应用Hopfield能量函数，从任意一个初始状态开始，在每次迭代后都能满足dE/dt≤0，网络的能量将会越来越小，最后趋于稳定点dE/dt=0.因此，可以把优化问题中的目标函数和约束条件与之相联系，建立适当的神经网络.当网络达到平衡点，意味着能量函数达到极小点，系统满足约束条件下目标函数的极小值.

本文将电力系统中有关谐波电流变量的目标函数转换为CHNN网络的能量函数，并将其变量与网络状态相对应，应用于实际检测.

1.2 电力系统中谐波电流的CHNN模型

假设在电力系统中，某一相流进非线性负载的周期性非正弦交流电流可表示为:

式中:φj，Ij——第j次谐波的相角和幅值(j=1，2，… ，N);

ω——基波角频率.

式(3)还可以表示为:

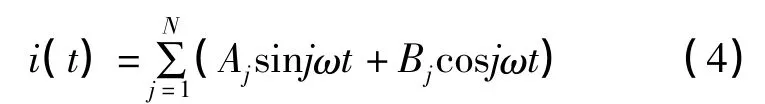
式中:Aj=Ijcosφj，Bj=IjsinIj.

将各次谐波的幅值和相角用Ai和Bi表示，则有:

设在某一采样时间tk时刻得到的采样值为dk(k=1，2，…，n，n 是采样次数).建立 Hopfield神经网络谐波检测电路，tk时刻的谐波i(tk)为:

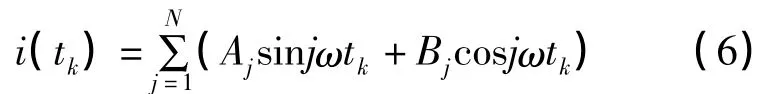
谐波测量要求准确性和实时性，在这里表现为i(tk)无限接近dk，而且要求谐波检测电路能够迅速对采样数据进行处理，以得到各次谐波参数.通过建立目标函数，利用Hopfield能量函数对目标函数进行优化计算，使i(tk)与dk的差值最小.

在谐波检测中，谐波电流的期望值为i(tk)，谐波电流的实际值为采样值 dk，建立目标函数［7］:

设ω已知，而tk也是确定的，因此cosjωtk和sinjωtk成为未知量Aj和Bj的系数.定义向量:

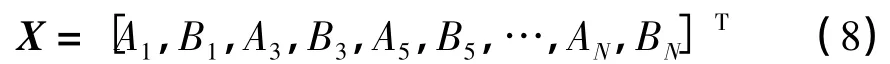
利用Hopfield能量函数对目标函数进行处理，要使i(tk)与dk的差值最小，即目标函数最小，定义能量函数:

能量函数E是向量X的函数.将dE/dt≤0的条件转化为对状态或输入向量求导的条件:

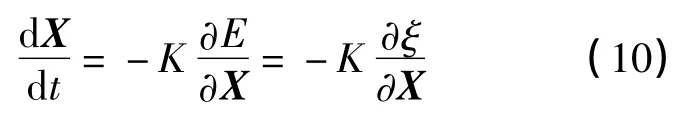
式中:K——积分系数.

即可推导出Aj和Bj的表达式为:

当CHNN网络的谐波电流检测模型达到稳定时，i(tk)无限接近dk，达到了谐波检测的目的.将模型稳定时的向量 X=［A1，B1，A3，B3，A5，B5，…，AN，BN］T代入式［11］和式［12］中，即可求出基波和各次谐波的幅值和相角.

2 谐波电流检测的仿真验证

2.1 基于CHNN的仿真分析

根据实际系统谐波的分布规律，建立了一个由若干谐波构成的谐波源:

标准谐波源见图2.谐波源在0.1 s时出现谐波，同时产生跳变.对该谐波源建立以Hopfield网络为基础的检测模型，检测出的各谐波波形及其对应相角分别见图3和图4.

由图3和图4不难看出，在选择了合适的积分系数(K=－380)和初始值(幅值和相角均为零)后，各次谐波所对应的幅值和相角均在较短的时间(半个基波周期)内趋于稳定，并且最终给出准确的计算结果，其中有关各次谐波的相角在调节过程中比幅值调节的震荡大一些，但也满足一般情况下对谐波分析准确性和实时性的要求.

图2 标准谐波源

图3 各次谐波的幅值

图4 各次谐波的相位

2.2 初始值对参数分析的影响

根据Hopfield理论，无论初始值在何种状态下，其内部的自适应算法均可以通过自动换算识别出最终的逼近能量函数为零的状态，也就是说初始值不应当决定输出值.在这种状态下若赋予初始值一个合理的范围，则不应当影响其收敛范围.此外，还可通过改变初始值观察仿真输出波形的收敛结果.将初始值由0改为6的输出结果见图5，其中为了简化仿真，将各次谐波的输入幅值和相角均改为6.

通过输出波形不难发现，在改变输入初始值的情况下系统依然在短时间内达到了准确的稳定输出，同时其震荡与前者相差并不大，对整个系统并无较大的影响.

图5 改变初始值后的幅值输出曲线

2.3 改变积分值对输出结果的影响

在输出参数的表达式中，比例积分系数K对系统的收敛与否起到了至关重要的作用.为观察K对整个系统的影响，本文选择了在两个不同的积分系数K的作用下的输出情况，见图6.

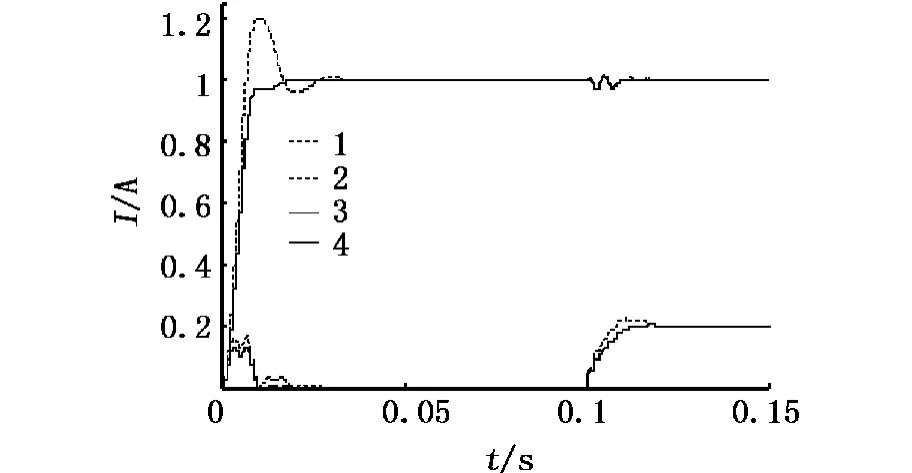
图6 改变积分常数后的输出曲线

图6中，曲线1和曲线2为积分系数K=－600时的基波和5次谐波幅值，曲线3和曲线4为积分系数K=－380时的基波和5次谐波幅值.

不难发现，K在很大程度上决定了输出的震荡程度及稳定时间，当K处于一定范围内时并不影响输出波形的准确性，但当K=－600时基波和5次谐波的幅值震荡明显加大，且需计算更多的次数才能达到稳态输出，若K的变化更大时甚至会影响到该输出波形参数的准确性，并有可能导致参数输出不收敛.因此，在实际谐波的检测过程中有必要结合谐波电流在正常范围值内所给出的经验积分值K，以防止影响参数输出的收敛性和稳定性.

3 结论

(1)采用本文所述的方法可实时地检测出各次谐波的幅值和相位，当谐波电流出现瞬时跳变时，半个周期内即可检测出跳变的各次波形，同时对于某些具有特殊要求的补偿装置来说，可以通过观察特殊次谐波，以有针对性地进行补偿;

(2)在各次波形特别是基波电流未知的情况下，可以随意设置初始值，因为初始值的给定并不影响自适应网络自我调整的过程，一样可以给出准确的波形参数;

(3)在大多数情况下积分系数K应当是一个固定范围内的值，因此有必要根据实际经验选择合适的积分系数K，否则，会对算法的收敛和震荡造成一定的不利影响.

［1］王兆安，杨君，刘进军.谐波抑制和无功功率补偿［M］.北京:机械工业出版社，1998:15-20.

［2］肖湘宁，徐永海.电能质量问题剖析［J］.电网技术，2001(3):67-69.

［3］李圣清，朱英浩，周有庆.电网谐波检测方法的综述［J］.高电压技术，2004(3):39-41.

［4］RUKONUZZAMAN M，NAKAOKA M.Single-phase shunt active power filter with harmonic detection［J］.IEEE Proceedings-Electric Power Applications，2002(5):343-350.

［5］柴旭峥，文习山，关根志.一种高精度的电力系统谐波分析算法［J］.中国电机工程学报，2003，23(9):67-70.

［6］丁士圻，郭丽华.人工神经网络基础［M］.哈尔滨:哈尔滨工程大学出版社，2008:10-50.

［7］王萍，邹宇，郭翠双.基于Hopfield神经网络的谐波电流检测方法［J］.天津大学学报，2007，40(12):1 431-1 435.