电力系统稳定器在抑制系统低频振荡中的应用
赵 璐
(上海电力学院电力与自动化工程学院,上海 200090)
由于电力系统规模的不断扩大,各区域电网的互联可以使电力系统更加经济可靠地运行.但同时,大规模的互联系统也带来了许多复杂的问题,如发电机组之间的功率动态振荡,特别是在互联系统的联络线上,这种振荡的表现更为突出.由于这种振荡的频率较低,一般在0.2~2.5 Hz范围内,因此称之为低频振荡[1].低频振荡严重时会导致系统解列或失去稳定,是大型电力系统互联时产生的最严重的系统稳定问题之一.系统中的弱耦合导致的弱阻尼是产生低频振荡的主要原因,而高发大倍数快速励磁系统则进一步加重了负阻尼的现象.因此,采取合理措施提高系统阻尼、抑制系统低频振荡是非常有必要的.
目前,国际上抑制低频振荡最常见的方法是励磁系统附加稳定控制,其中电力系统稳定器(Power System Stabilizer,PSS)因其具有成本低、结构简单、效果好等优点而得到广泛应用[2,3].
1 PSS的工作原理
PSS的工作原理如图1所示.

图1 PSS工作原理
图1中,φ2为PSS环节本身对特定频率的输入信号产生的相位移;φ3为励磁系统对PSS调节信号ΔPSS产生的相位滞后角度.系统信号经过励磁系统后,所产生的电磁力矩T1滞后于Δδ一个角度ø1,从图1可以看出,T1在ω轴上的分量是负值,即其提供负的阻尼.为了消除这种负阻尼,需要附加一个控制信号,即PSS信号.
以取功率增量作为输入信号的PSS为例来说明其作用原理.功率增量ΔP与Δδ反向,从图1可以看出,要使机组稳定运行,并使最后合成的电磁转矩T∑在ω轴上的分量为正值,即提供正的阻尼,则由PSS调节信号产生的电磁力矩T2必须落在第一象限,因此必须对PSS的输入信号ΔP提供一个相位滞后.
只要适当调整PSS输出信号的相位及放大倍数,就可以使最后的合成电磁力矩提供正的阻尼力矩和正的同步力矩.
在原理上,PSS的输入信号可以是与电功率有关联的任何量,包括 Δω,Δδ,Pe,ΔP,Δf等,本文利用转子角速度和电功率信号作为PSS的输入信号,克服了单输入信号的缺点,同时使PSS达到更好的抑制效果[1].
2 MATLAB仿真建模
2.1 PSS 系统建模
电力系统稳定器是由隔直、超前-滞后校正、放大、限幅等4个环节组成的,因此将Simulinkcotinuous中的Transfer Fcn传递函数模块,Math Operations中的Sum信号叠加模块和Gain增益模块,Signal Routing中的Manual Switch手动开关模块,Sources中的 Ground地输出信号模块,以及Discountinuities中的Saturation限幅模块连接在一起,形成PSS系统仿真模型,如图2所示.

图2 PSS系统仿真模型
2.2 励磁系统模型
励磁系统的仿真模型如图3所示.
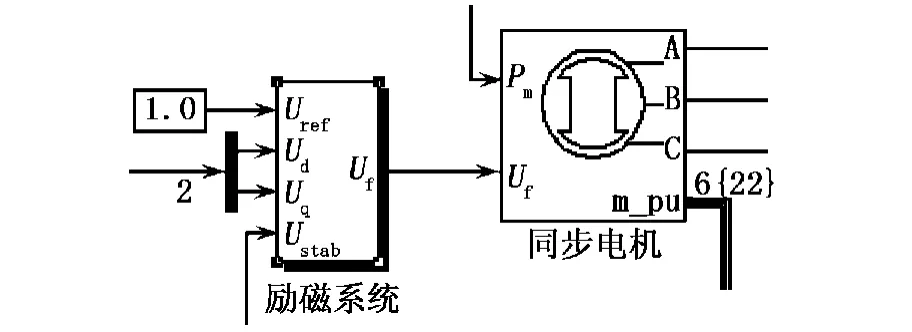
图3 励磁系统仿真模块
图3中,与输入端参考电压Uref连接的是值为1的常数模块,此处也可以连接一个单位阶跃函数Step模块.利用同步发电机信号分离器中的Us_qd输出端将励磁系统的定子、转子电压输入端分离成Ud和Uq两路,接入励磁系统.
2.3 同步发电机接线
同步发电机的仿真模块如图4所示.由图4可以看出,在水力汽轮机的wref与Pref输入端接入两个常数模块,we,Pe0,dw分别以同步发电机信号分离器中的wm,Pe0,dw信号量作为输入,输出端Pm与同步发电机的Pm输入端相连接,为同步发电机提供机械功率.同步发电机的ABC 3相分别 连接负载和变压器,模拟现实的输电配电网络.
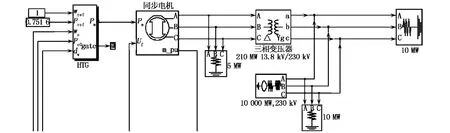
图4 同步发电机仿真模块
2.4 系统仿真模型
在Simulink-Sinks中的Scope示波器模块中,分别命名所要测的信号量,并将各模块对应接上,观察低频振荡对这些参数的具体影响,接线如图5所示.
本文同步发电机采用的是标幺制模块,所以测得的数据是标幺制形式[4].

图5 整个系统仿真模型
3 仿真试验及结果分析
首先,利用Matlab的sisotool指令观察系统的传递函数,确定其固有频率,并根据固有频率和系统伯德图选择合适的整定频率和整定相角,计算出将要滞后或者超前的角度,配置PSS的超前滞后单元参数.其次,选择PSS的输入信号,根据不同的信号特点确定PSS系统隔直单元的参数.最后,从小到大增加PSS的增益模块,观察发电机有功信号输出是否开始持续振荡,以确定整个系统的临界振荡值 励磁系统和同步发电机可以使用默认参数或者根据现场实际参数进行配置,选择合适的仿真时间和算法进行最后的仿真.
双击手动开关能够改变励磁系统中PSS的投、切状态,PSS投入前后发电机的有功波形如图6和图7所示.当系统未投入PSS时,发电机各参数持续振荡,在10 s时仍能看到持续小振荡.但当投入PSS后,可以清楚地看到,在2~4 s时系统各个参数便逐渐趋于稳定,说明PSS系统能够有效快捷地抑制系统的低频振荡,提高了发电质量[6].

图6 未投入PSS时发电机的有功波形
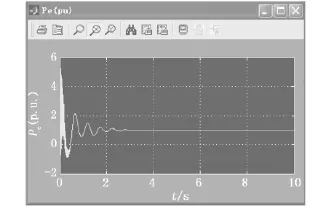
图7 投入PSS后发电机的有功波形
由图6和图7可以看出,在未投入PSS时,有功波形的最大上下峰值分别为6,-2,之后波形衰减幅度并不明显,在10 s的仿真时间内仍发生上下幅值相差比较大的振荡,在最后时刻仍然能够看到波形还没有完全稳定.但当投入PSS后,能够发现有功波形的最大上下峰值为6,-1,之后有明显的衰减,下个波峰和波谷上下幅值相差较小,幅值也明显比原波形小得多,在仿真进行约3 s后波形已趋于稳定,并持续输出1(p.u.),完全快速地抑制了低频振荡.
4 结语
本文应用Matlab实现了对电力系统稳定器、励磁系统和同步发电机的仿真,并进行了大量的参数配置,从而实现了通过改变PSS参数来有效抑制低频振荡,这将大大减少现场调试PSS所花费的时间,具有较高的实用价值.
本文主要研究了在单机系统中PSS抑制低频振荡的效果,还可以根据此模型的原理及方法建立模拟多机系统的模型,以及观察多机系统中各个PSS之间的影响、抑制低频振荡的效果等.随着数字技术及仿真技术的发展,PSS将会逐渐趋于智能化,从而能更快速、有效地抑制低频振荡.
[1]石辉,张勇军,徐涛.我国智能电网背景下的低频振荡应对研究综述[J].电力系统保护与控制,2010,38(24):13-15.
[2]薛禹胜,郝思鹏,刘俊勇.关于低频振荡分析方法的评述[J].电力系统自动化,2009,33(3):26-28.
[3]BOUKARIM G E,WANG S,CHOW J H,et al.A comparison of classical robust and decentralized control designs for multiple power system stabilizers[J].IEEE Transaction on Power System,2000,15(4):36-39.
[4]刘建,王晶,翁国庆.电力系统的MATLAB/SIMULINK仿真与应用[M].西安:西安电子科技大学出版社,2008:156-160.
[5]吴峰,鲁晓帆,陈维荣,等.电力系统稳定器参数优化的研究[J].电力系统保护与控制,2010,38(5):28-30.
[6]杨俊新,马进,陶华.基于电力系统混合仿真的低频振荡误差校正策略[J].电力系统自动化,2010,34(8):18-21.

