带色散项的高阶非线性Schr¨odinger方程的精确解

曹瑞

(菏泽学院数学系,山东 菏泽 274000)

带色散项的高阶非线性Schr¨odinger方程的精确解

曹瑞

(菏泽学院数学系,山东 菏泽 274000)

对一类带色散项的高阶非线性Schr¨odinger方程的精确解进行研究.通过行波约化,将一类带色散项的高阶非线性Schr¨odinger方程化为一个高阶非线性常微分方程.再借助于计算机代数系统Mathematica通过构造非线性常微分方程的精确解,成功获得了一系列含有多个参数的包络型精确解,当精确解中参数取特殊值时可以得到两种新型的复合孤子解.并讨论了这两种孤子解存在的参数条件.

高阶非线性Schr¨odinger方程;精确解;孤立波解

1 引言

物理学中许多重要现象的数学模型都是非线性发展方程,一般来说这些非线性方程很难求得精确解.非线性发展方程的精确解在研究非线性物理现象中起着至关重要的作用.寻找非线性发展方程精确解的方法一直是数学家和物理学家研究的热点问题,几十年来,提出了许多求解非线性发展方程的方法,例如Painleve截尾展开法[12],齐次平衡方法[34],双曲函数法[56],sine-cosine方法[7],CK方法[8],Jacobi椭圆函数展开方法[9]以及作为 Jacobi椭圆函数展开方法一般化的F-展开方法[1012],利用这些方法得到非线性发展方程许多丰富的精确解,包括孤立波解,激波解,周期波解等.最近,提出了一种新的构造精确解的G'/G展开方法[13].运用这个方法,成功地获得了大量非线性发展方程的精确解.

作为介绍这种方法应用的例子,本文构造了光纤中一类具有三阶色散项与三次非线性项的高阶非线性薛定谔(Schr¨odinger)方程(HNLS)的精确解

这个方程描述了光纤中超短光脉冲的传输,其中ψ=ψ(z,t)是慢变包络振幅,z为传输距离,t为时间,α1,α2和α3分别表示与群速度,自相位调制和三阶色散有关的实参数.含α4的项代表着自陡峭效应对光脉冲传输的影响,含α5的项代表着自频移所产生的拉曼散射的影响.

经典的非线性薛定谔方程

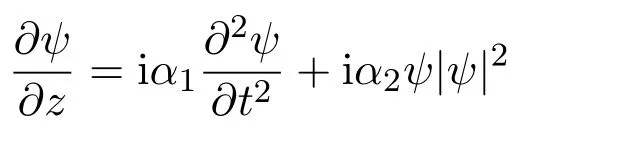
描述了光脉冲在光纤中的群速色散效应与非线性克尔效应的关系,当二者的相互作用达到平衡时,脉冲就演化为光孤子.但是,对于飞秒级的光脉冲而言,脉冲的带宽可与其载波频率相比拟,光纤的高阶色散效应(如三阶色散等)和高阶非线性效应已不能忽略.当方程(1)中α3=α4=α5=0时,方程(1)就变为经典的非线性薛定谔方程(NLS).本文将对方程(1)进行研究,以希望得到一些新结果.近年来,许多科研工作者从不同的方向分析研究了HNLS,得到了一系列的数值解,包括亮孤子和暗孤子,并已发现在负色散区(α1＜0)存在亮孤子解,而在正色散区(α1＞0)存在暗孤子解[1415].文献[16]通过一系列分析计算,发现了HNLS一种新型组合孤子,并且在一定参数条件下,该组合孤子仍然可以在光纤中稳定传输.文献[17]利用扩展的双曲正切函数法,获得了方程(1)的多组显示精确行波解.当α3,α4,α5不为0时,虽然已经获得了方程(1)的一些精确孤波解,但本文是第一次利用扩展的G'/G展开方法对方程(1)的精确孤波解进行新的研究,获得了一些新的复合孤波解.

本文安排如下:第二部分,详细介绍构造高阶非线性Schr¨odinger方程的精确解的一般表达式过程;第三部分,给出参数取特殊值时高阶非线性Schr¨odinger方程的孤立波解、双曲函数解、三角函数解以及有理函数解;第四部分,得出一些结论.

2 精确解的一般表达式

这里N通过平衡给定方程(6)中的最高阶偏导数项和非线性项来确定.根据N+2=3N,可得N=1.即方程(6)有下列形式的解:

将(8)式代入方程(6),那么常微分方程(6)的左边可化为关于φ,φ的级数,合并φ,φ的相同幂次,令每一项的系数为零,得到关于a0,a1,b1,A,B,C,λ,µ的一个非线性代数方程组.借助于计算机代数系统Mathematica求解得到的这个代数方程组.将这些结果代入(6)式,并利用二阶常系数微分方程的通解.得到非线性方程(1)含有多个参数的精确解的一般形式.

下面分三种情形来讨论:

情形一(双曲函数解) 若λ＜0,那么方程(7)有通解:

3 其它形式的解

注1 当所得精确解的一般表达式中参数取其它值时,可以获得更为丰富的精确解,这里限于篇幅不再列出.

4 结语

本文应用行波变换,并结合常微分方程通解统一构造了具有三阶色散、自陡峭效应和自频移效应的高阶非线性Schr¨odinger方程的三种不同类型的精确解.当精确解中参数取特殊值时可以得到新型的复合孤立波解.这些精确解丰富了高阶非线性Schr¨odinger方程精确解的解系,而且有助于物理上对这类方程的研究.从所得解中可以看出,光脉冲的缓变包络振幅ψ(z,t)具有形如(15),(16)式所示的新型的精确解.并进一步讨论了新型的精确解存在的参数条件,指出了(15)式所示的解存在于负三阶色散区域,而(16)式所示的解存在于正三阶色散区域.这些新解的获得将为光纤通信问题的研究,提供理论依据.从求解过程来看,此方法借助于计算机代数系统Mathematica构造非线性发展方程的精确解更直接、更高效,还可以用来求解其他的非线性发展方程包括高维方程,这方面的研究正在进行中.

[1]Weiss J,Tabor M,Carnevale G.The Painleve's property for partial di ff erential equations[J].J.Math.Phys., 1983,24(3):522-526.

[2]张解放,陈芳跃.截断展开方法和广义变系数KdV方程[J].物理学报,2001,50(9):1648-1650.

[3]Wang M L,Zhou Y B,Li Z B.Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J].Phys.Lett.A,1996,216:67-75.

[4]Parkes E J,Du ff y B R.An automated tanh-function method for fi nding solitary solutions to nonlinear evolution equations[J].Comput.Phys.Commun.,1996,98:288-300.

[5]郭冠平,张解放.关于双曲函数方法求孤波解的注记[J].物理学报,2002,51(6):1159-1162.

[6]张睿,张玉春,王彬弟.应用拓展双曲函数方法求KP方程的新精确解[J].纯粹数学与应用数学,2010,26(4):651-655.

[7]Yan C T.A simple transformation for nonlinear waves[J].Phys.Lett.A,1996,224:77-84.

[8]刘秀玲,李金花,胡斌.(2+1)维浅水波方程的新精确解[J].纯粹数学与应用数学,2008,24(4):666-669.

[9]Liu S K,Fu Z T,Liu S D,et al.Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J].Phys.Lett.A,2001,289:69-74.

[10]曹瑞.改进的F-展开方法和藕合Klein-Gordon方程的精确解[J].兰州大学学报:自然科学版,2007,43(6):112-116.

[11]赵云梅,芮伟国.Zhiber-Shabat方程的孤立波解与精确波解[J].纯粹数学与应用数学,2008,24(2):283-288.

[12]Zhou Y B,Wang M L,Wang Y M.Periodic wave solutions to a coupled KdV equations with variable coefficients[J].Phys.Lett.A,2003,308:31-36.

[13]Wang M L,Li X Z.The(G'/G)-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics[J].Phys.Lett.A,2008,372:417-423.

[14]Mollenauer L F,Stolen R H,Gordon J P.Experimental observation of picosecond pulse narrowing and solitons in optical fi bers[J].Phys.Rev.Lett.,1980,45(9):1095-1098.

[15]Emplit P,Hamaide J P,Reynaud F,et al.Picosecond steps and dark pulse through nonlinear single mode fi bers[J].Opt.Commun.,1987,62(6):374-379.

[16]田晋平,何影记,周国生.高阶非线性薛定谔方程的一个新型孤波解[J].光子学报,2005,34(2):252-254.

[17]吴晓飞.修正高阶非线性薛定谔方程的显示行波解[J].激光与红外,2005,35(10):785-787.

Exact wave solutions for the higher-order nonlinear Schr¨odinger equation with a dispersion term

Cao Rui
(Department of Mathematics,Heze College,Heze 274000,China)

Exact solutions of the higher-order nonlinear Schr¨odinger equation with a dispersion term are studied.By traveling wave reduction,the higher-order nonlinear Schr¨odinger equation are transformed into nonlinear ordinary di ff erential equation,and then by constructing a series of exact solutions of nonlinear ordinary di ff erential equation,many envelope type exact wave solutions containing multiple parameters are obtained for the higher-order nonlinear Schr¨odinger equation with the aid of computer algebraic system Mathematica.when parameters are taken speci fi c values,two new kind of soliton solution are obtained.And the conditions of the existence of soliton solution are discussed.

the higher-order nonlinear Schr¨odinger equation,exact wave solutions,solitary wave solutions

O175.29

A

1008-5513(2012)01-0092-07

2011-02-10.

菏泽学院科学研究基金(XY07SX01).

曹瑞(1979-),硕士,讲师,研究方向：应用偏微分方程.

2010 MSC:35Q55