一类非线性偏微分方程的四阶格子Boltzmann模型

周志强,何郁波

(怀化学院数学系,湖南 怀化 418008)

一类非线性偏微分方程的四阶格子Boltzmann模型

周志强,何郁波

(怀化学院数学系,湖南 怀化 418008)

通过Chapman-Enskog展开技术和多尺度分析,建立了一种新的D1Q4带修正项的四阶格子Boltzmann模型,一类非线性偏微分方程从连续的Boltzmann方程得到正确恢复.统一了KdV和Burgers等已知方程类型的格子BGK模型,还首次给出了组合KdV-Burgers,广义Burgers-Huxley等方程的四阶LBGK模型.数值模拟结果表明了该模型的有效性和稳定性．

非线性偏微分方程;格子Boltzmann模型;Chapman-Enskog多尺度展开

1 引言

近年来,格子Boltzmann方法(简称LBM)成功应用于某些复杂的非线性演化方程,如对流扩散方程、反应扩散方程、Kuramoto-Sivashinsky方程等.文献[1-3]采用D1Q4模型分别研究了KdV-Burgers方程、组合KdV方程、MKdV方程,文献[4]则采用D1Q5模型研究一类非线性偏微分方程,他们都得到了较好的结果.本文采用D1Q4模型构造出一个带修正项和源项的四阶格子Boltzmann显示迭代格式.通过这个模型,一大类非线性偏微分方程从连续的Boltzmann方程得到正确恢复.该方法不仅涵盖了文献[1-3]中的全部模型,还给出了组合KdV-Burgers方程,广义KdV方程,广义Burgers-Huxley方程,广义Burgers-Fisher方程等多种非线性偏微分方程的格子BGK模型.相比文献[4],因为少了一个速度方向,数学推导过程要简单许多,内存和时间消耗也少一些.数值模拟结果表明该模型数值精度与文献[4]相当;适当选取模型参数,模型具有长时间的计算稳定性.

2 四阶格子Boltzmann模型

一维含源非线性偏微分方程如下:

3 数值模拟

表1 Burgers-Huxley方程数值解与解析解的整体相对误差

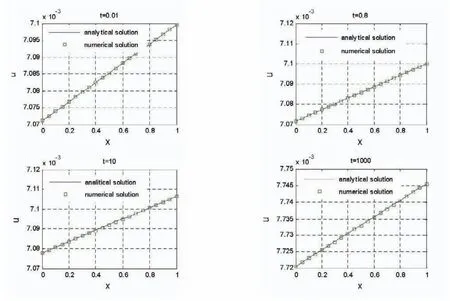
图1 Burgers-Huxley方程在t=0.01,0.8,10,1000时刻数值解与解析解对照,实线代表解析解,□号为数值解

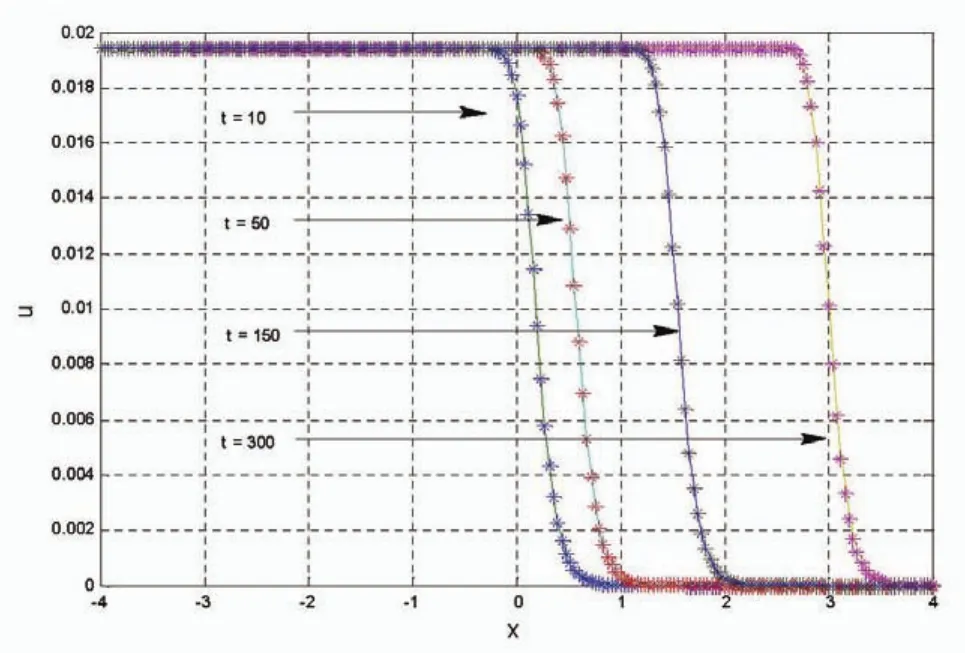
图2 KdV-Burgers方程在t=10,50,150,300时刻数值解与解析解对照,实线代表解析解,*号为数值解

参考文献

[1]Ma C F.A new lattice Boltzmann model for KdV-Burgers equation[J].Chin.Phys.Lett.,2005,22(9):2313-2315.

[2]何郁波,马昌凤．组合KdV方程带修正函数的格子Boltzmann模型[J].应用数学学报,2007,30(6):1040-1046.

[3]马昌凤,唐嘉,陈小红.模拟mKdV方程的格子BGK模型[J].应用力学学报,2007,24(4):519-521.

[4]赖惠林,马昌凤.非线性偏微分方程的高阶格子BGK模型[J].中国科学:G辑,2009,39(7):913-922.

[5]Javidi M.A numerical solution of the generalized Burger's-Huxley equation pseu-dospectral method and Darvishi's preconditioning[J].Appl.Math.Comput.,2006,175:1619-1628.

A fourth order lattice Boltzmann model for nonlinear partial di ff erential equation

Zhou Zhiqiang,He Yubo
(Department of Mathematics,Huaihua University,Huaihua 418008,China)

A new D1Q4 fourth order lattice Boltzmann model with amending function is presented for nonlinear partial di ff erential equations.By using Chapman-Enskog expansion technique and multiple-scale analysis,a class of NPEs are restored correctly from continuous Boltzmann equation.This paper not only gives a uni fi ed lattice BGK model for the well-known equation such as KdV and Burgers equation,but also fi rstly gives a fourth order LBGK model for the combined KdV-Burgers equation,generalized Burgers-Huxley equation,etc.Numerical simulation results show that the method described in this paper is e ff ective and stable.

nonlinear partial di ff erential equations,lattice Boltzmann model,Chapman-Enskog expansion

O241

A

1008-5513(2012)01-0029-07

2011-08-17.

湖南省教育厅科研基金(07C505).

周志强(1974-),硕士,副教授,研究方向：数值计算.

2010 MSC:35Q53