有关p-级数与交错级数的和的研究*
梁双凤 刘 鹏 杨 胜
(1.楚雄师院学院数学系,云南 楚雄 675000;2.楚雄师院学院经济管理及计算机应用系,云南 楚雄 675000)
1.两个引理
(1)若m是偶数,则
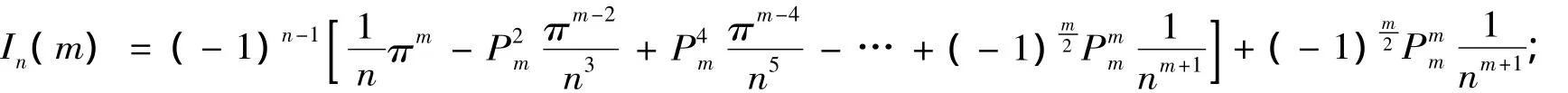
(2)若m是奇数,则
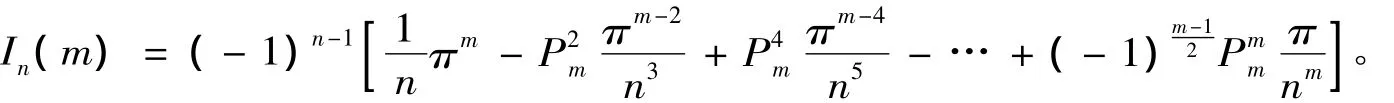
证明 显然
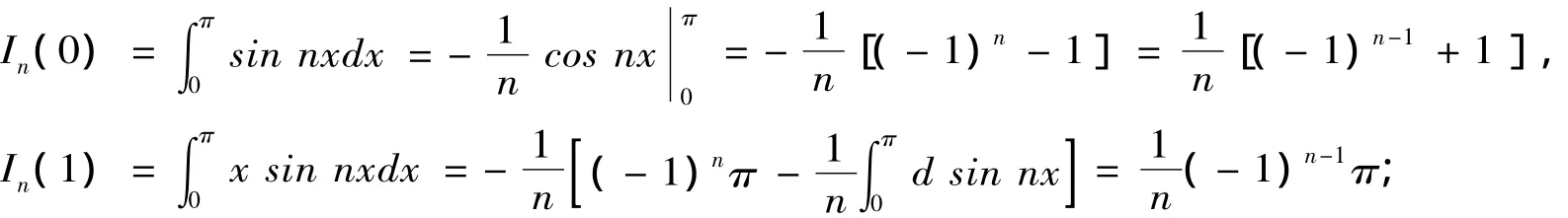
当m≥2时,
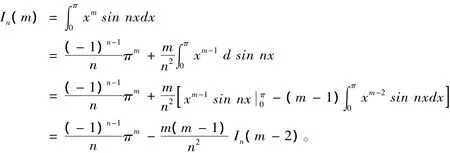
即得出递推式
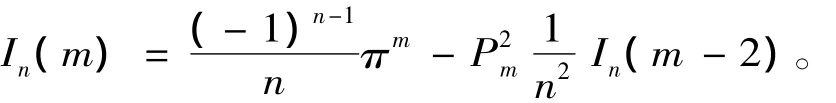
利用此递推式,可以得出
(1)当m是偶数时,有
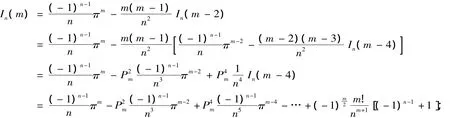
即
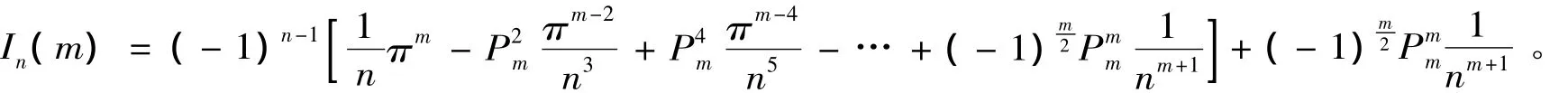
(2)当m是奇数时,同理可以证明
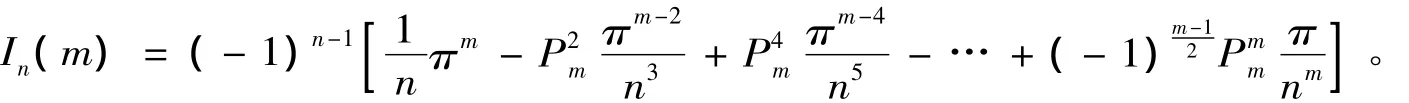
引理2 设f(x)是周期为2π的函数,它在一个周期[-π,π]上的表达式为f(x)=xp。若p是偶数,则函数f(x)的傅里叶级数中的系数bn,a0,an分别为
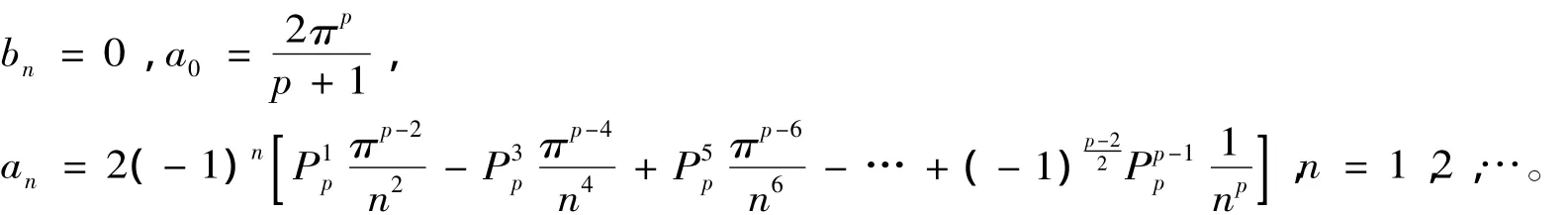
证明 由于f(x)=xp是R上的连续的偶函数,所以傅里叶级数中的系数bn,a0,an分别为[1]
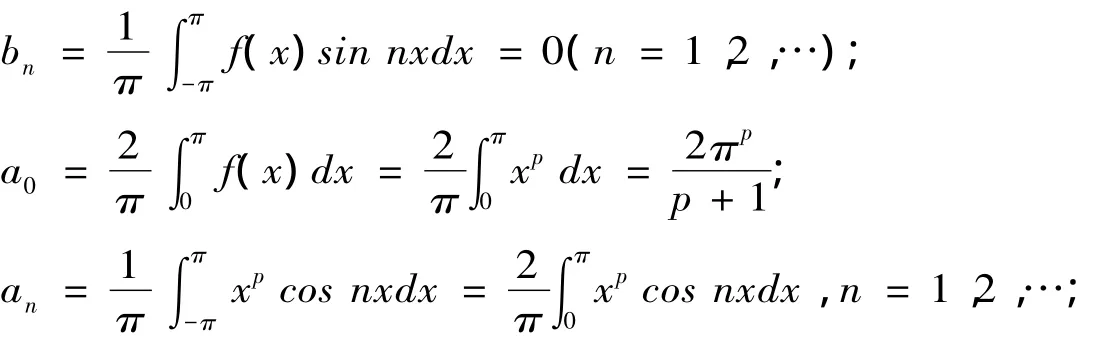
由引理1知
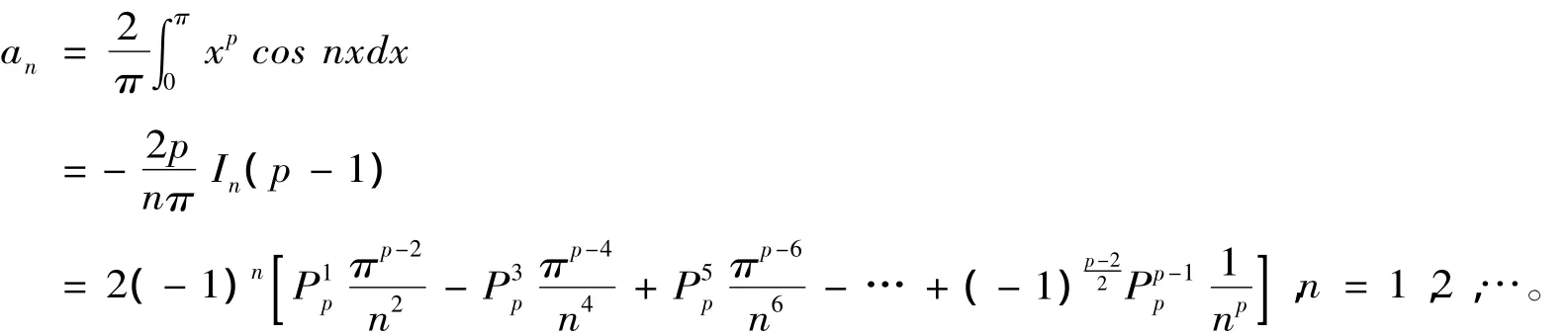
显然,当p=2时,函数y=x2在区间[-π,π]上展开的傅里叶级数为[1]
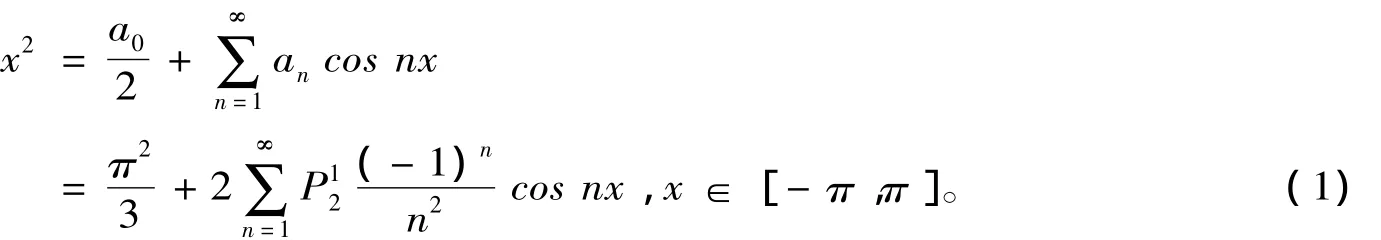
在(1)式中令x=π,则可得出

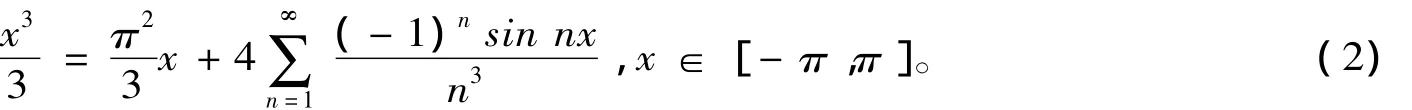

用同样的方法,我们可以得出

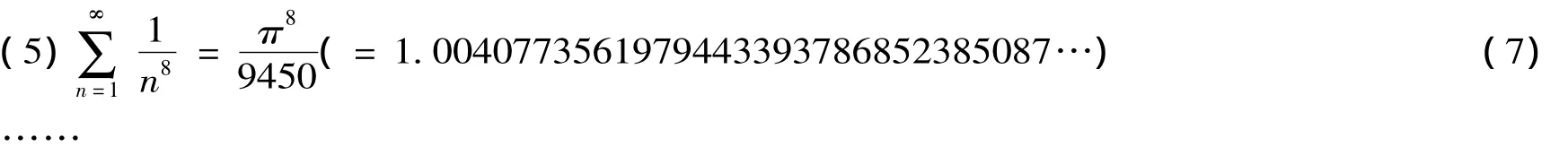
2.两类级数的和的递推公式
2.1 当p是偶数时,p-级数的和的递推公式
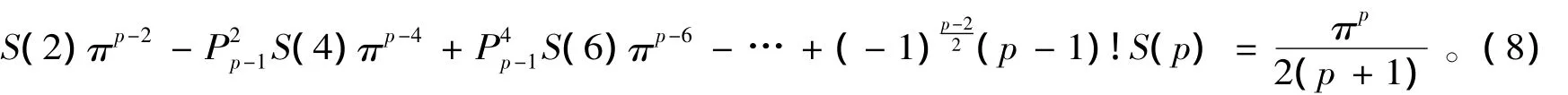
证明 当p是偶数时,根据引理2知道,偶函数f(x)=xp的傅里叶级数为
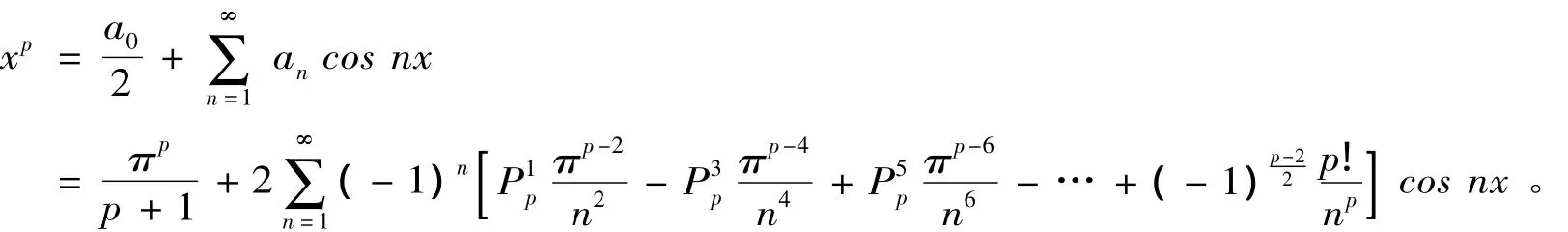
令x=π,则由上式得到
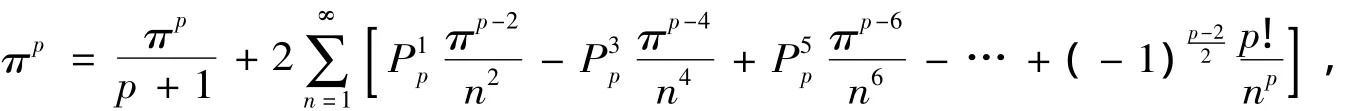
从而得到当p为偶数时求p-级数的和的递推式(8)


2.2 当p为奇数时,交错级数的和及其递推式
当p为奇数时,我们有下面的结果:

证明由引理2知道,当p是偶数时,偶函数f(x)=xp的傅里叶级数为
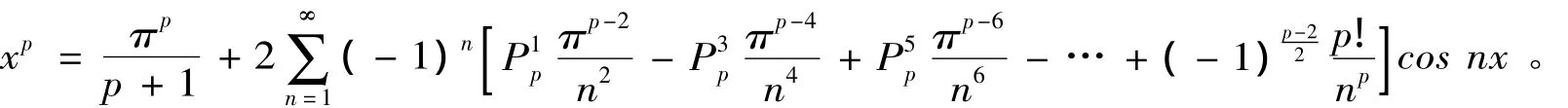
对上式两边关于x求导得
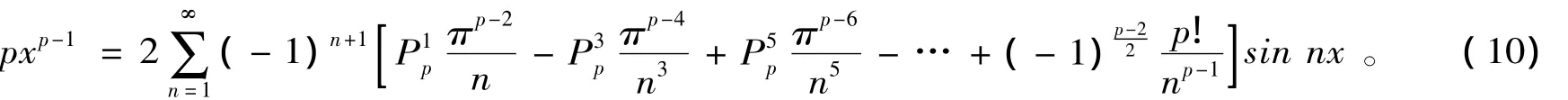
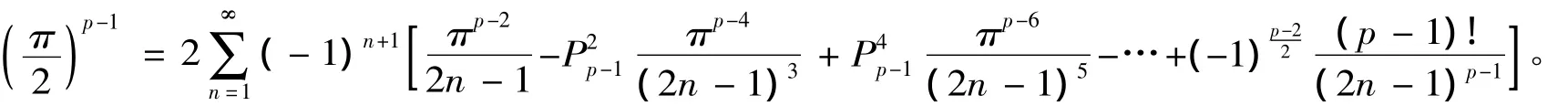

在(10)中,当p=2时,可得到函数y=x在区间(-π,π)上展开的傅里叶级数为
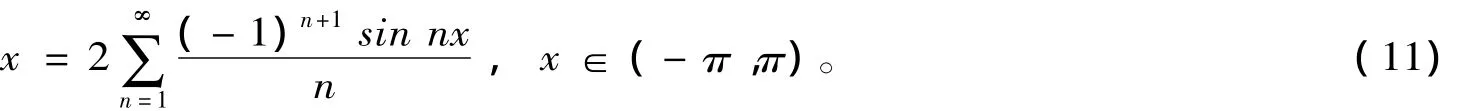

用同样的方法,我们可以求出
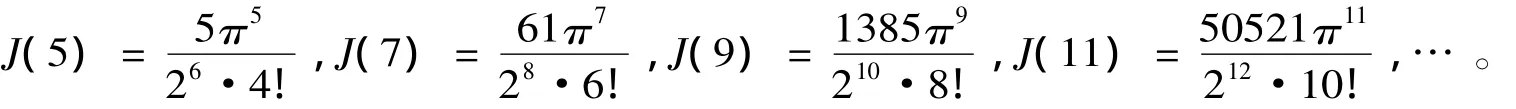
3.当p为奇数时,对级数的和的研究
当p(p>1,p∈N)为奇数时,p-级数的和无法用准确公式表示出来.但我们可以借助MATLAB应用软件,用数学实验的方法得出其和的无穷近似值,或在满足一定计算精确度要求的前提下,利用近似公式,求出其和的近似值。
首先用MATLAB应用软件可求出
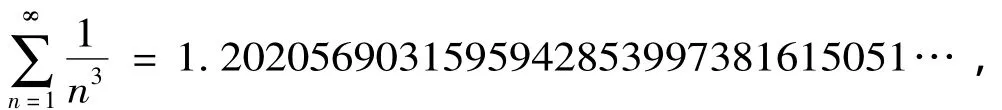
即
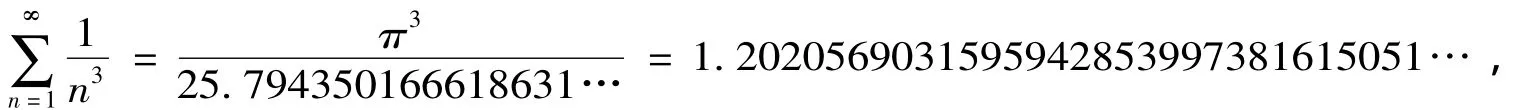
同样,借助MATLAB软件,我们可以得到
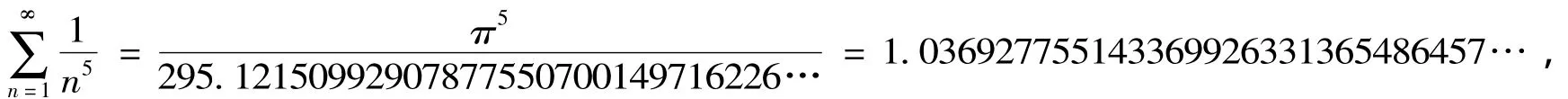

如果我们假设
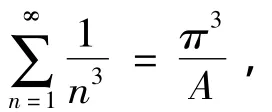
现在可以确定的是:A是一个无理数,但它无法用准确值表示出来。
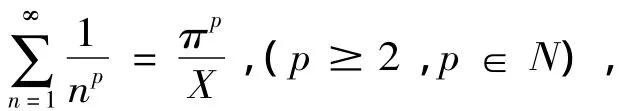
则当p为偶数时,X为有理数;当p为奇数时,X为无理数。
实际上,不仅仅当p为奇数时,p-级数的和无法用准确值表示出来,而且当p不是整数时,我们一般也很难求出其和的准确值。此时,我们可以考虑在满足精确度要求的前提下,用近似值来表示其和。
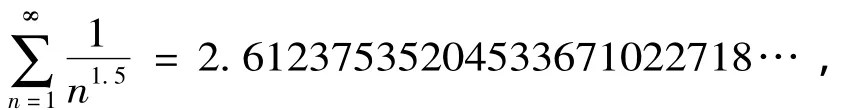
或者我们借助求p-级数的和的近似公式[2]
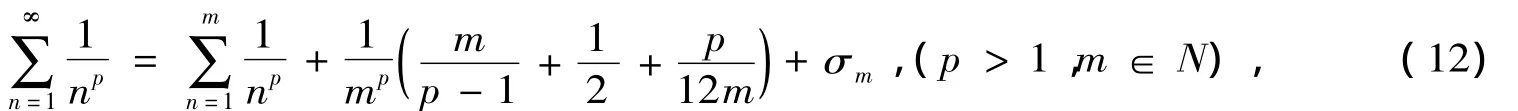
其中
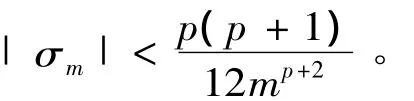
利用公式(12),取m=10,则可得到
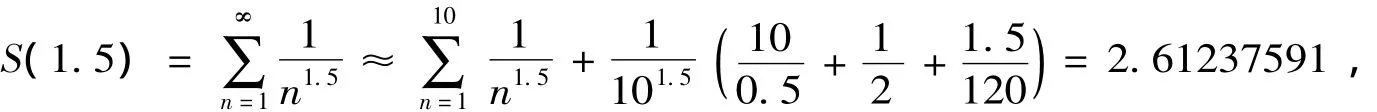
其中误差|σm|< 9.88 ×10-5。
同样可得到,
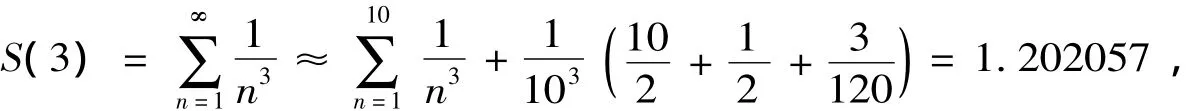
其中误差 |σm|< 10-5。
[1]同济大学数学系编.高等数学 (下)[M].北京:高等教育出版社,2010:302—303.
[2]朱文辉,张亭.p-级数的和的近似公式 [J].大学数学,2005,6(3):114—115.

