基于小波－卡尔曼滤波的基波分量提取

孙旭霞，郭永胜

（西安理工大学自动化与信息工程学院，西安710048）

目前，大多数继电保护以故障后的稳态基频分量作为判据，如何从故障暂态信号中快速、准确地对基频电流、电压进行估计是微机保护算法面临的主要问题。在通常情况下，估计精度的高低取决于数据窗的长短。常见的微机保护算法有全波傅里叶算法、半波傅里叶算法、最小二乘算法与卡尔曼滤波算法。全波傅里叶算法能滤除所有整次谐波分量，稳定性好，但数据窗需1个周期，使其对近区故障无法快速反应［1，2］。半波傅里叶算法能够在半个数据窗内对故障基频分量进行估算，但其对低频分量的抑制效果不好，而且对偶次谐波有一定的放大作用，在完全利用故障后数据进行滤波时，该算法的时间响应波动较大［3］。最小二乘算法从频域角度看相当于全零点滤波器，但当故障信号模型和干扰信号的分布特性难以准确估计时，其滤波精度以及暂态时延无法保证［4］。卡尔曼滤波算法是具有时变数据窗特性的滤波算法，适用于平稳过程也适用于非平稳过程，对噪声有很好的抑制作用，被广泛应用于频率跟踪、谐波分析等场合，但其滤波精度以及暂态时延也无法同时兼顾［5～6］。

本文提出了一种卡尔曼滤波结合小波变换的基波分量提取方法，即用卡尔曼滤波模型估计基波分量特征，结合sym4小波变换高频分量模极大值来捕捉故障发生时刻，在故障发生时刻更新增益系数和误差协方差矩阵，从而减少了卡尔曼滤波模型的响应时间，保证了微机保护对故障的快速响应。

1 算法原理

1.1 基于卡尔曼滤波估计提取基波的原理

1.1.1 Kalman滤波的基本原理

故障电压、电流信号的Kalman谐波模型有多种，文中采用如下线性模型［5，8，10］。

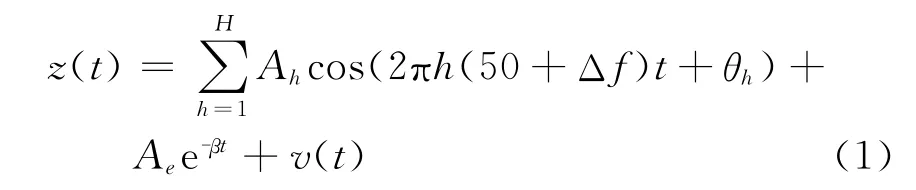
其中：H为故障信号的最高谐波次数（本文中考虑H ＝5），Δf基波频率偏移；Ah各谐波幅值；Ae、β为衰减直流分量的幅值及时间常数；θh为h次谐波初始相位；v（t）为噪声信号。

取状态变量：

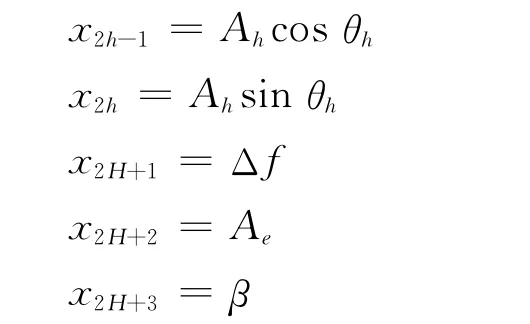
状态方程为

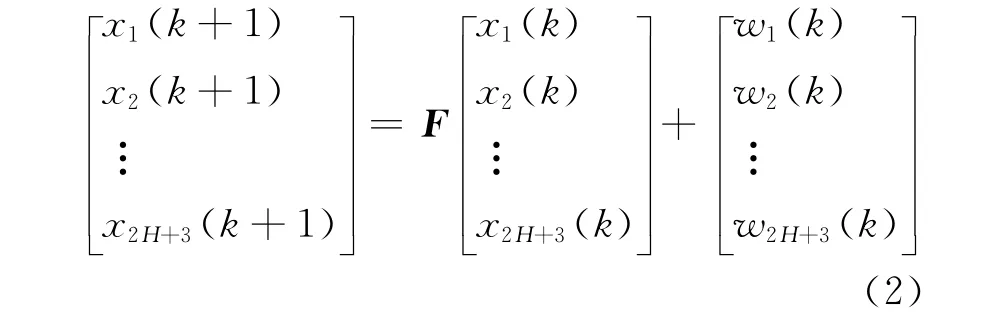
测量方程为

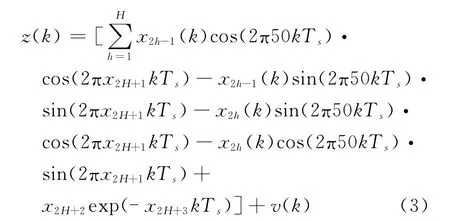
xi（k）、xi（k＋1）为k、k＋1时刻的系统状态，wi（k）、v（k）是均值为0、方差分别为σw2、σv2白噪声，且满足：

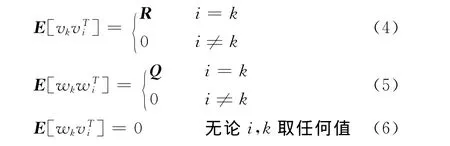
1.1.2 滤波参数选取

滤波参数选取是决定卡尔曼滤波算法性能好坏的关键。常用的方法是大量试凑，直到系统稳定，对系统调试很不利。经过分析和总结，本文给出以下参数选取思路。

由于在协方差矩阵中缺少充分的非对角元素统计信息，通过大量仿真实验后，证明在非对角元素为非零的情况下，相对于对角元素的值对系统稳态的影响可以忽略，因此假设三个协方差矩阵为对角矩阵是成立的。所以通常情况下将协方差矩阵非对角元素设为零，这样很大程度上减少了未知参数的个数。协方差矩阵（0）表征了系统的动态信息，改变（0）中对角元素的值，可以改变系统瞬态性能，而系统稳态性能不受影响。Q表征了系统模型的统计特性，增加Q中元素的值，等价于增加系统噪声或增加系统参数的不确定性，从而使得增益矩阵Gf增大，加大了系统校正权值，提高了系统动态性能和稳态值。矩阵R表征了测量噪声，增加R中元素的值，意味加大测量噪声的影响，同时使Gf减小，减弱系统校正权值，降低了系统瞬态响应和稳态值。所以矩阵Q和R的选取具有矛盾性，二者进行选取时，应视具体情况权衡而定。

1.2 小波变换及其模极大值

设任意函数f（x）∈L2（R）为平方可积函数组成的Hilbert空间，小波变换可定义为［9］

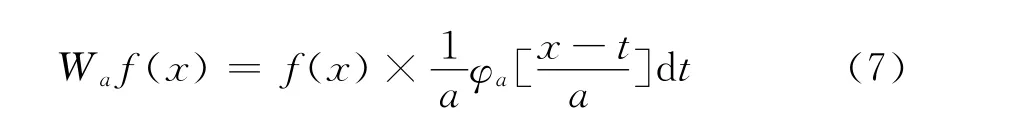
①定义域是紧支撑的，即只有小的局部非零定义域。

②容许条件，即

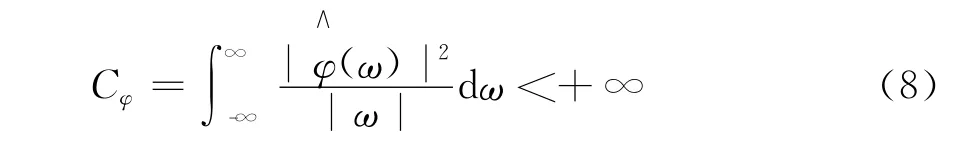
在某一固定尺度a下，若∀x∈（x－δ，x＋δ），有｜Wsf（x）｜≤｜Wsf（x0）｜成立，则称x0为小波变换的模极大值点，｜Wsf（x0）｜称为模极大值。

信号的突变点可由小波变换的模极大值来反映，本文中对基波分量估计值进行小波变换，当故障发生时，基波分量估计值会出现瑕疵，在小波高频分量中会出现模极大值，可确立故障信号的发生时刻［12］。

本文中选用sym4小波，因为symlets小波是正交的时域紧支小波，此特性使其具有良好的计算性；自身良好的对称性可使信号的分解与重构避免失真。在symlets小波系列中，由于sym1小波的滤波器不连续，不能使用；sym2、sym3小波的滤波器长度较短，对信号奇异点的敏感性不强。综合考虑数据窗长度及对奇异点的敏感性，确定采用sym4小波来监测基波分量的突变时刻［9］。

算法整体流程如图1所示。

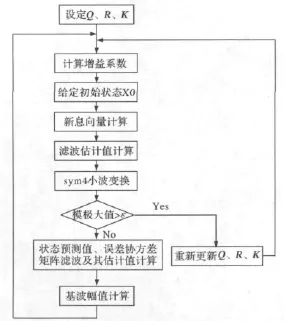
图1 小波 －卡尔曼提取基波分量流程Fig.1 Flow chart of fundamental component detection using wavelet and Kalman filter

2 算例分析

为深入分析该算法的可行性，本文进行了大量仿真验证。限于篇幅，只针对如下几种电流信号模型进行仿真分析。仿真中，采样频率为10kHz，R＝0.1001［10，11］。

2.1 基波频率

基波信号频率在一定范围内动态波动，信号模型如下：

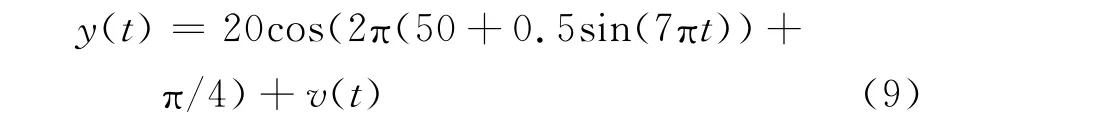
由图2可知，在基波频率存在微小波动时，本算法对频率波动有一定鲁棒性，不因频率波动而出现较大的波动值，而全周傅氏算法则出现较大的波动。且由图2（c）可看出，基波分量估计值重构高频分量不因频率波动而发生突变。

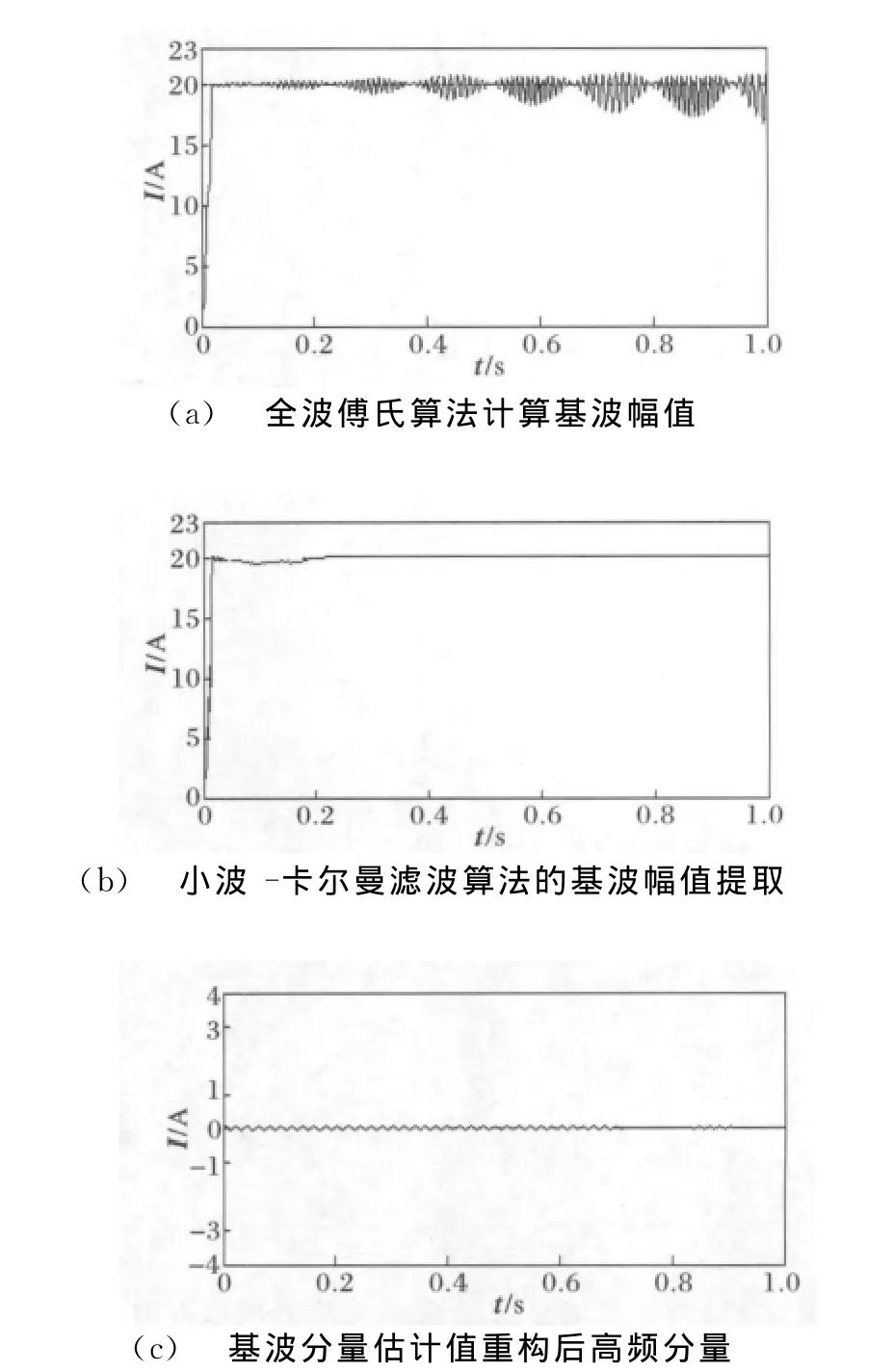
图2 频率波动时幅值计算及高频分量Fig.2 Magnitude calculation and high frequency component with frequency fluctuation

2.2 基波幅值

运行过程中在某一时刻发生故障，基波幅值变化，暂态信号中混有高次谐波及衰减直流分量。

2.2.1 故障信号模型1

信号模型为式（10），滤波响应如图3所示。

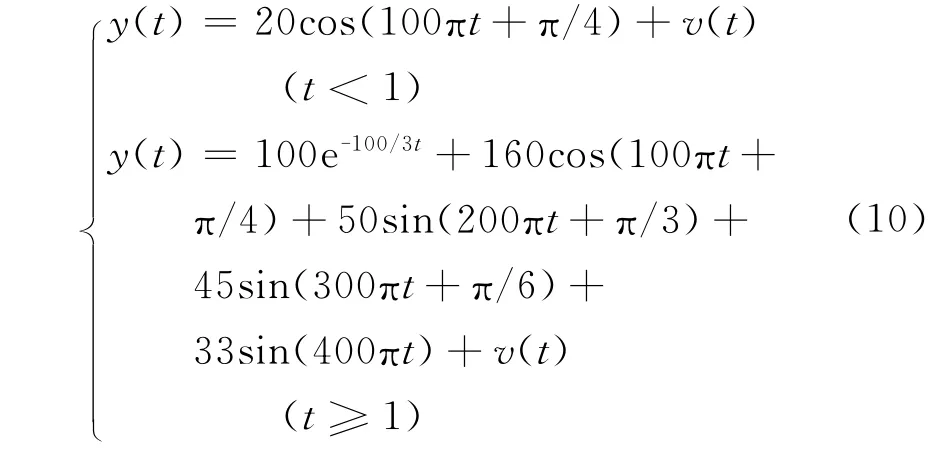
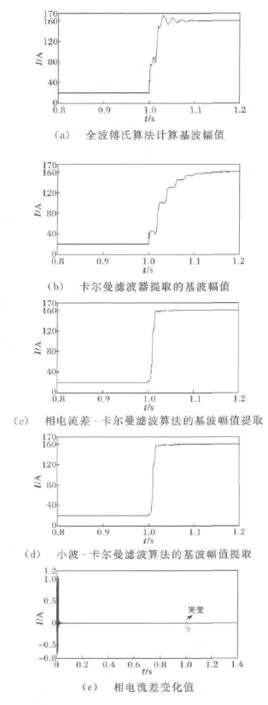
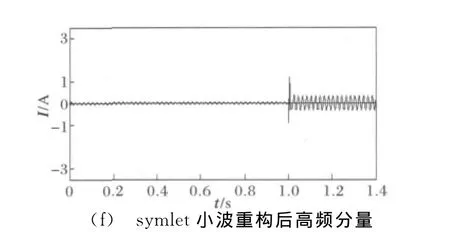
图3 系统运行过程中发生故障Fig.3 Fault in the period of running

2.2.2 故障信号模型2

信号模型为式（11），滤波响应如图4所示。

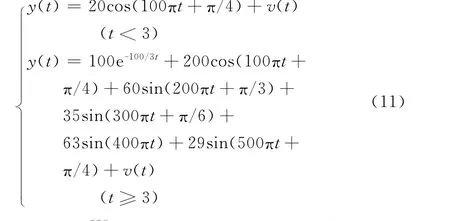
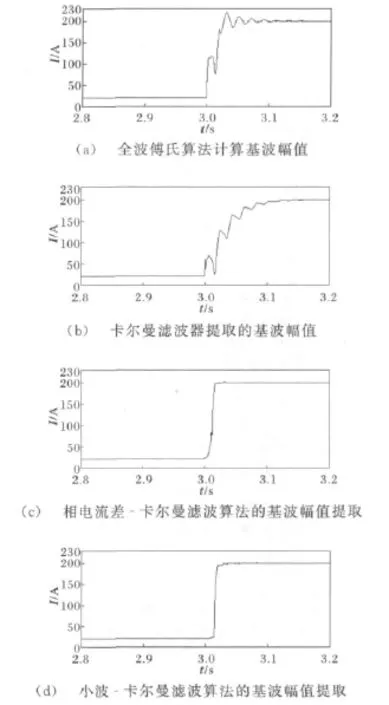
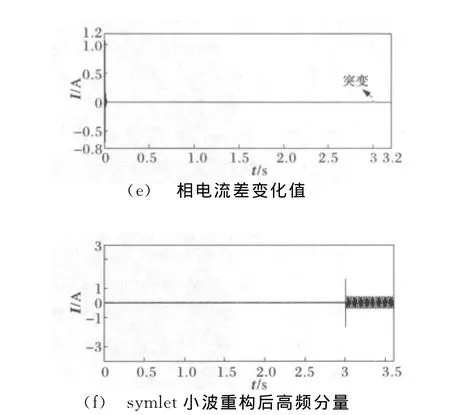
图4 系统运行过程中发生故障Fig.4 Fault in the period of running

由图3、4可知，在发生故障时，与全波傅氏算法相比，采用相电流差 －卡尔曼滤波算法和小波－卡尔曼滤波算法受衰减非周期分量及高次谐波的影响小，能够更准确地提取基波分量，使卡尔曼滤波算法响应速度明显加快。但由图3（e）、4（e）可看出，相电流差 －卡尔曼滤波算法在基波突变时刻得出的相电流差跳变值较小，且其明显小于卡尔曼滤波在开始适应无故障信号所得到的相电流差值，所以在应用此算法时必须跳过卡尔曼滤波算法自身适应时间再做判定，以免造成误判。但由图3（f）、4（f）可看出，小波－卡尔曼滤波算法在故障发生时刻，基波分量估计值重构高频分量有较大的突变，且明显大于卡尔曼滤波在开始适应无故障信号所得到的重构高频分量值，充分体现了小波算法“数学显微镜”的美誉。因此，本算法不仅能准确地提取基波分量并且很大程度上加快了卡尔曼滤波器的响应，而且能精确捕捉故障发生时刻，不受卡尔曼滤波器自身适应过程的影响。

2.3 仿真测试

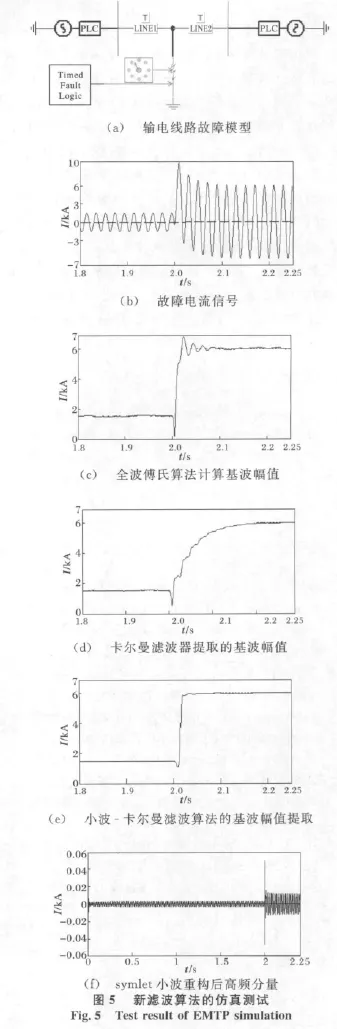
针对某750kV输电线路EMTP仿真单相接地故障时的电流波形以及新算法对仿真数据的滤波结果。

新滤波算法的仿真测试模型及结果如图5所示。

另外，本算法还用于线路短路故障并做了大量的验证工作，结果表明该算法能精确捕捉故障发生时刻，可以较准确地提取基频分量，保证了微机保护的精确实时动作。

3 结语

由仿真结果表明：本算法对基波频率在一定范围动态波动时具有很好的鲁棒性，而这一特点更符合实际系统中基波信号的运行规律，即频率大部分时间在较小的范围内（一般系统频率波动范围为（50±0.2）Hz，当系统容量较小时，频率波动范围为（50±0.5）Hz）［5］波动。当发生故障时，本算法可精确捕捉故障发生时刻，不因噪声影响而产生误差，并且在一定程度上缩短了卡尔曼滤波模型的响应时间，达到对基波分量精确快速的提取。与全波傅氏算法比较，证明了该算法在提取基波分量的精度及实时性上都有一定优越性。因此，本算法具有响应速度快、滤波效果好的特点，能满足继电保护快速跳闸和准确动作的要求。

［1］ Yu S－L，Gu J－C.Removal of decaying DC in current and voltage signals using a modified Fourier filter algorithm［J］.IEEE Trans on Power Delivery，2001，16（3）：372－379.

［2］ Gu Jyh－cherng，Yu Sun－Li.Removal of DC offset in current and voltage signals using a novel Fourier filter algorithm［J］.IEEE Trans on Power Delivery，2000，15（1）：73－79.

［3］ Gu Y，Kezunovic M，Chen D S.Simplified algorithms or removal of the effect of exponentially decaying DC－offset on the Fourier algorithm［J］.IEEE Trans on Power Delivery，2003，18（3）：711－717.

［4］ 黄瀛，何奔腾（Huang Ying，He Benteng）.继电保护中最小二乘算法的最佳噪声模型（Study on the optimal noise model of least error square algorithm for relay protection）［J］.电力系统自动化（Automation of Electric Power Systems），2004，28（9）：31－35.

［5］ 张静，徐政（Zhang Jing，Xu Zheng）.基于卡尔曼滤波误差的电能质量扰动检测（Power quality disturbances detection based on Kalman filter residuals）［J］.电力系统及其自动化学报（Proceedings of the CSUEPSA），2006，18（5）：25－30.

［6］ Styvaktakis Emmanouil，Gu Irene Y H ，Bollen Math H J.Voltage dip detection and power system transients［C］∥Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference，Vancouver，Canada：2001.

［7］ Gu Irene Yu－Hua，Styvaktakis Emmanouil.Bridge the gap：signal processing for power quality applications［J］.Electric Power Systems Research，2003，66（1）：83－96.

［8］ Kose Neslihan，Salor Ozgul，Leblebicioglu Kemal.A Kalman filter based approach for light flicker evaluation of power systems［C］∥IEEE 17th Signal Processing and Communications Applications Conference，Antalya，Turkey：2009.

［9］ 李中伟，程丽，佟为明（Li Zhongwei，Cheng Li，Tong Weiming）.Symlets小波幅值算法研究（Study of Symlets wavelet amplitude algorithm ）［J］.电力自动化 设 备 （Electric Power Automation Equipment），2009，29（3）：65－68.

［10］ 李斌，李永丽，贺家李（Li Bin，Li YongLi，He Jiali）.一种提取基波分量的高精度快速滤波算法（Accurate and fast filtering algorithm for fundamental component）［J］.电力系统自动化（Automation of Electric Power Systems），2006，30（10）：39－43，74.

［11］朱桂英，龚乐年（Zhu Guiying，Gong Lenian）.傅氏算法在微机保护应用中的探讨（Discussion on application of Fourier algorithm in microcomputer protection）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2005，17（4）：41－43，93.

［12］ 江红胜，侯勇，朱晓光（Jiang Hongsheng，Hou Yong，Zhu Xiaoguang）.基波分量的一种快速提取方法及其在有源滤波器中的应用（Novel fundamental detection method and its application in the active power filter）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2004，16（6）：34－37.