用特征网络优化开关频率的SVPWM控制方法
王 翠 孟志强
(1. 湖南大学电气与信息工程学院 长沙 410082 2. 南昌工程学院机械与电气工程学院 南昌 330006)
1 引言
目前国内外对空间矢量调制算法的研究已取得了一定的成果,文献[1,2]直接利用空间矢量等效为参考矢量,这种算法简单,实现也比较容易,在低频应用中可以得到很好的负载电压波形。文献[3-8]讨论了一些算法,它们降低了开关器件的损耗,用频率较低的开关器件得到较高的调制频率,但它们都限于分析三电平以下的具体电路,其中处理得最多的是三电平电路。
文献[9]研究一般的n级l电平逆变电路,它通过坐标变换,把输出电压矢量端点坐标变换到整数网格上,并使用四舍五入的方法逼近参考电压,显著地减少了计算工作量,但其逼近的误差较大。文献[10,11]提出了分段调制法,即先找到扇区,然后用扇区的三个顶点分时制地合成参考电压,这种方法提高了逼近的精度,但也增加了电路中开关器件的切换次数。文献[12]运用基本切换降低了逆变器的开关频率,但文献没有对切换路径进行系统的分析。
本文基于文献[9,12]的研究成果,在α ′ β ′ 坐标平面上,利用特征四边形和特征网络的概念,针对三级七电平逆变器,给出沿特征网络在扇区的顶点之间进行切换的算法。最后,通过仿真和实验验证该算法的开关频率被大大降低,且输出电压能很好地逼近参考电压。
2 三相三级七电平逆变器电路的拓扑
图1是三相三级七电平逆变器电路拓扑,每个逆变单元的输出电压在E、0和-E之间变动,E为逆变单元的输入直流电压。每相逆变器输出的相电压 ua、ub、uc包含±3E、±2E、±E、0等 7个电平。
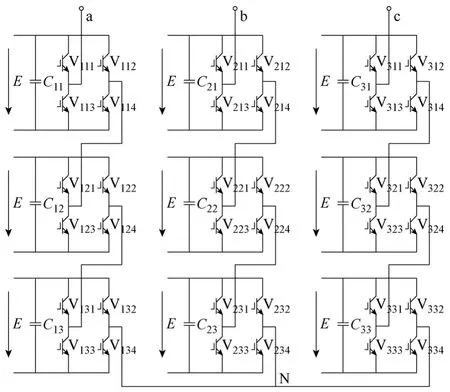
图1 三相七电平逆变器的拓扑Fig.1 Three-phase 7-level inverter topology
根据文献[9],逆变器输出相电压(ua, ub,uc)在 α ′ β ′ 坐 标 平 面 上 可 以 分 解 为 : 两 相 分 量(uα′, uβ′)。以E为基准归一化各个电压:a=ua/E、b=ub/E、c=uc/E、 α′ = uα′/E、 β′ = uβ′/E ,有

式中, a, b, c ∈{±3 , ±2, ±1 , 0} 。按式(1)在α ′ β ′ 平面上绘制两相分量(α ′、β ′)构成的矢量轨迹如图2所示,是一个倾斜45°的六边形内的离散点集,每个点代表一个分量(α ′、β ′ ),称为α ′ β ′ 平面上的基本矢量,所有基本矢量张成分量(α ′、β ′ )的矢量空间,称为α ′ β ′ 平面上的基本矢量空间。沿α ′和β ′方向,相邻点之间的距离等于一个电平。显然,逆变器开关的一次有效切换在α ′ β ′平面上表现为一个离散点的跳变。
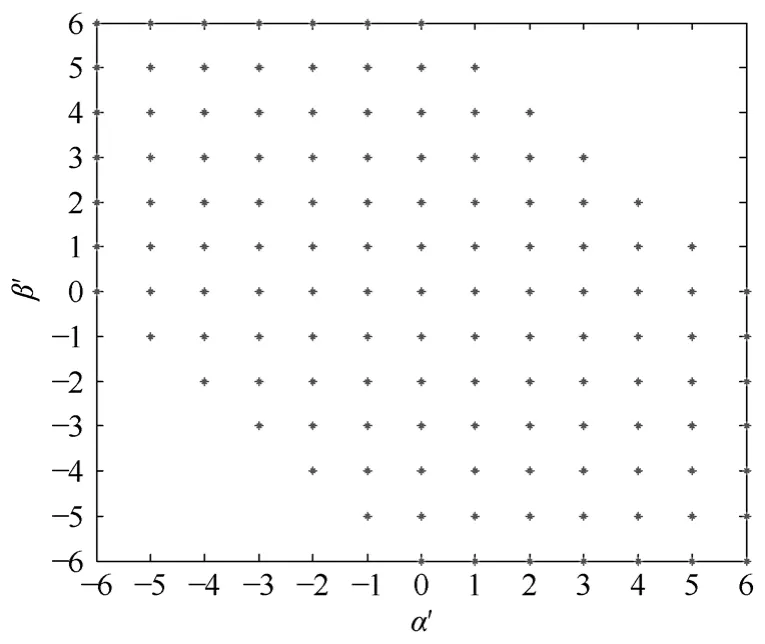
图2 α ′ β ′ 平面的基本矢量Fig.2 basic vector in α ′ β ′ coordinate plane
3 α ′ β ′ 平面上参考矢量的轨迹及其逼近扇区序列S
在三相逆变器中,逆变器输出相电压(ua, ub,uc)的波形常常是跟随参考电压(ura, urb,urc)的,设参考电压为峰值等于Ur的正弦波
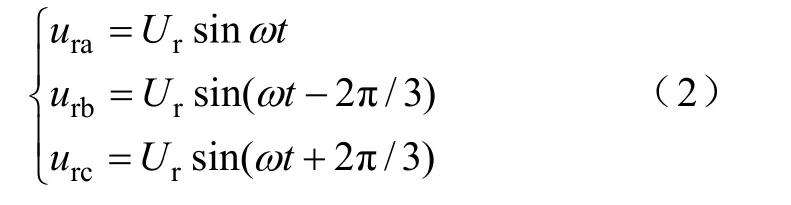
将参考电压变换到α ′ β ′ 平面上,得到对应的两 相 分 量 ( αr′, βr′ )

以 E 为基准归一化 urα′和 urβ′,αr′ = urα′/E ,βr′ = urβ′/E ,得

由此可知,参考电压在α ′ β ′平面上的轨迹为一椭圆,称为参考矢量,如图 3所示椭圆轨迹。以 n级逆变器为例, Ur= 2 nE/为最大的参考电压幅值,设 Ur=2 nmE/,改变m(0<m≤1)的大小可改变参考电压的轨迹,m即为调制系数,其值反映直流母线电压的利用率。
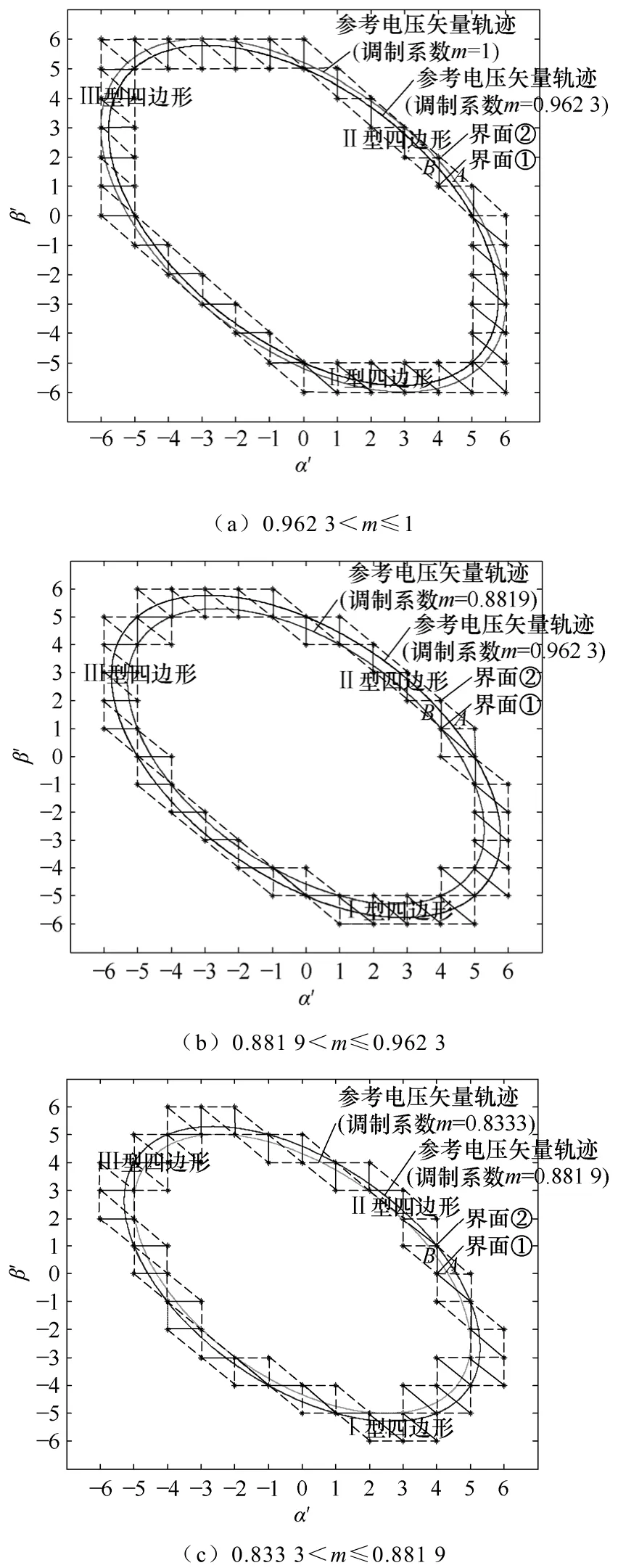
图3 基本矢量空间中扇区序列S的形状Fig.3 Figure of reference vector’s sector S in basic vector space
对逆变器开关切换的有效控制就是选择适当的基本矢量组合跟踪参考矢量,并使跟踪误差最小。一个基本矢量与沿α ′和β ′方向相邻的基本矢量构成一个直角三角形,称为扇区,如图3中的直角三角形A和B。参考矢量的瞬时值可以用扇区的三个顶点矢量(α ′、β ′)分时制地合成。控制逆变器的开关切换,就能改变扇区,实现对参考矢量的跟踪。用于逼近参考矢量轨迹的所有扇区组成扇区序列S,如图3中直角三角形组成的区域。改变调制系数m,即改变参考矢量的峰值 Ur,在α ′ β ′ 平面跟踪参考矢量的扇区序列存在三种可能,分别如图 3a~3c所示:图3a对应 0.9623<m≤1,图 3b对应 0.881 9< m≤0.962 3,图3c对应0.833 3<m≤0.881 9。图3中调制系数m范围的划分原则是使该范围内所有可能的参考矢量轨迹都具有相同的扇区序列。
4 扇区序列S的特征网络
调制算法的任务就是用扇区序列S的顶点逼近参考电压矢量,其中一个重要步骤是确定一种算法遍历S的全部顶点。观察图3中基本矢量空间的扇区序列 S可以看出,A、B两类三角形组成 I、II、III三种四边形(图3中的四边形,其对角线为实线)。
文献[12]已经证明,在扇区三角形的顶点之间切换找不到一条封闭的路径,在相邻两个扇区三角形组成的四边形的四个顶点之间切换可以找到一条封闭的切换路径,这样的四边形称为特征四边形。
由扇区序列S组成的、构成封闭切换路径的特征四边形顶点所对应的实现称为扇区序列S的特征网络。图3所示为特征四边形构成的特征网络。
5 优化开关频率的SVPWM调制算法
参考电压的采样点数会影响逆变器输出的性能,以及功率器件的开关次数。采样点太少不能充分利用电平数,因此,在本文的研究中要求每个三角形扇区内至少有1个采样点。
由于扇区序列S的特征网络遍历的路径都在该扇区所在的特征四边形的四边上,计算过程总是根据参考矢量的位置变动,依次遍历相应的特征四边形的顶点,因此可分成特征四边形内的切换和特征四边形之间的切换两部分来进行研究。
5.1 特征四边形内的切换顺序及切换次数估计
将特征四边形中两个三角形扇区共有的顶点称为该特征四边形的界面,如图3中的实线两端的点,并分别称为界面①和界面②。对应于相应界面的基本矢量称为接口矢量。显然,只有以界面为起点,才能用两次切换遍历扇区的三个顶点,否则至少需要三次切换。
先讨论取界面①为起点,沿着其四条边先后遍历该四边形内两个扇区的过程,如图3a所示。设扇区A和B内分别有Mj1和Mj2个采样点,而整个特征四边形内的采样点数为Mj=Mj1+Mj2。整个遍历过程为:沿扇区A的边遍历它的三个顶点,共Mj1次;如果 Mj1为奇数,将从界面②离开该扇区,否则从界面①离开该扇区;然后从界面②或界面①出发,沿着扇区 B的边遍历其三个顶点。显然,如果 Mj为奇数,将从界面②离开该四边形,否则从界面①离开该四边形。取特征四边形的界面②为起点的情况与此类似。
按照上述切换过程,在每个特征四边形内将扇区A的终点直接用作扇区B的起点,因而特征四边形内的总切换次数等于2Mj。
5.2 特征四边形之间的切换顺序及切换次数估计
从前面的结论可知,从第 j个特征四边形到第j+1个特征四边形之间的切换,实际上就是第j个特征四边形的终点界面到第j+1个特征四边形的起点界面之间的切换。显然,对应同类四边形之间的切换,前后两个特征四边形的对角线平行,则可以用1次基本切换来完成。对应不同类四边形之间的切换,前后两个特征四边形的对角线相交,视各自的终点和起点分布的情况,可能出现两种情况:第 j个特征四边形的终点界面和第 j+1个特征四边形的起点界面为同一个点,则这两个特征四边形间不需要切换;如果不是同一个点,这两个特征四边形间就需要2次基本切换。
对于第1种形状的特征网络,从图3a中可以看出,只有3处是在不同类的四边形之间进行切换,所以切换次数为

式中,ns表示总切换次数;Mj为对应特征四边形中的采样点数;J为特征网络中的特征四边形数。
对于图3b的特征网络,特例存在于三种四边形的两两分界线上,分界线两边的特征四边形位置出现了互换,共有9个分界面,即有9次需要在不同类型的特征四边形之间进行切换,所以
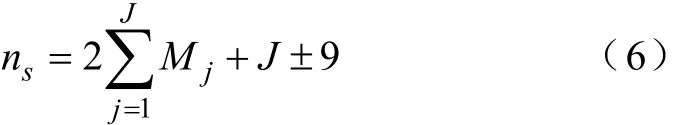
对于图3c的特征网络,特例存在于三种四边形的两两分界线上,分界线两边的特征四边形位置出现了互换,共有15个分界面,即有15次需要在不同类型的特征四边形之间进行切换,所以

6 仿真、实验研究及结果
本文以三级七电平级联逆变器主电路为例,对上述算法进行Matlab仿真。仿真用参考电压矢量的频率为 50Hz,参考电压矢量的调制系数 m=0.97,它具有图 3a类似的特征网络,特征四边形的个数J=33。选择每个扇区对应1个采样点,则每周波采样点数为 66。由式(5)可以求出,一个周期内三相电压总切换次数为
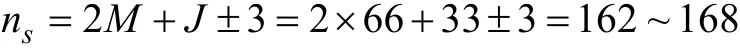
图4为仿真输出波形,图4b为线电压波形,线电压为13电平PWM调制波,其波形更加规则、对称,且更接近于正弦波。图4a是一个周期相电压波形,a、b、c三相相电压的变化次数为53、53、54,三相相电压一个周期的变化次数为53+53+54=160,与理论分析的结果一致。

图4 开关频率优化算法仿真波形Fig.4 Simulation waveforms of the switch frequency optimized algorithm
为了验证该优化调制算法的正确性,搭建了三级七电平逆变器电路,实验参考电压频率为50Hz,参考电压的调制系数为m=0.97,每单元逆变器整流侧输入交流电源为 110V,负载每相串联两个 25W白炽灯,Y形联结。逆变桥开关管采用IRF460,驱动采用 AVAGO公司的光耦 HCPL3120,由于光耦之间不能共地,系统用了27个DC15V电源模块,另外控制系统用一个DC5V电源模块。控制系统采用 ARM(飞利浦公司的 LPC2119)+FPGA(Altera Cyclone系列的 EP1C3T144C8)的模式,LPC2119用于采样参考电压,计算参考矢量,确定参考矢量所在扇区,并计算扇区三角形顶点矢量及其实现,完成优化算法,输出三相电平信号给FPGA。FPGA接收三相输出电平值转换为各级联单元中每个开关器件的PWM控制信号,并计算死区时间。图5为实验波形,从图5a可以读出其中两相电压在一个周期的变化次数分别为53、55。
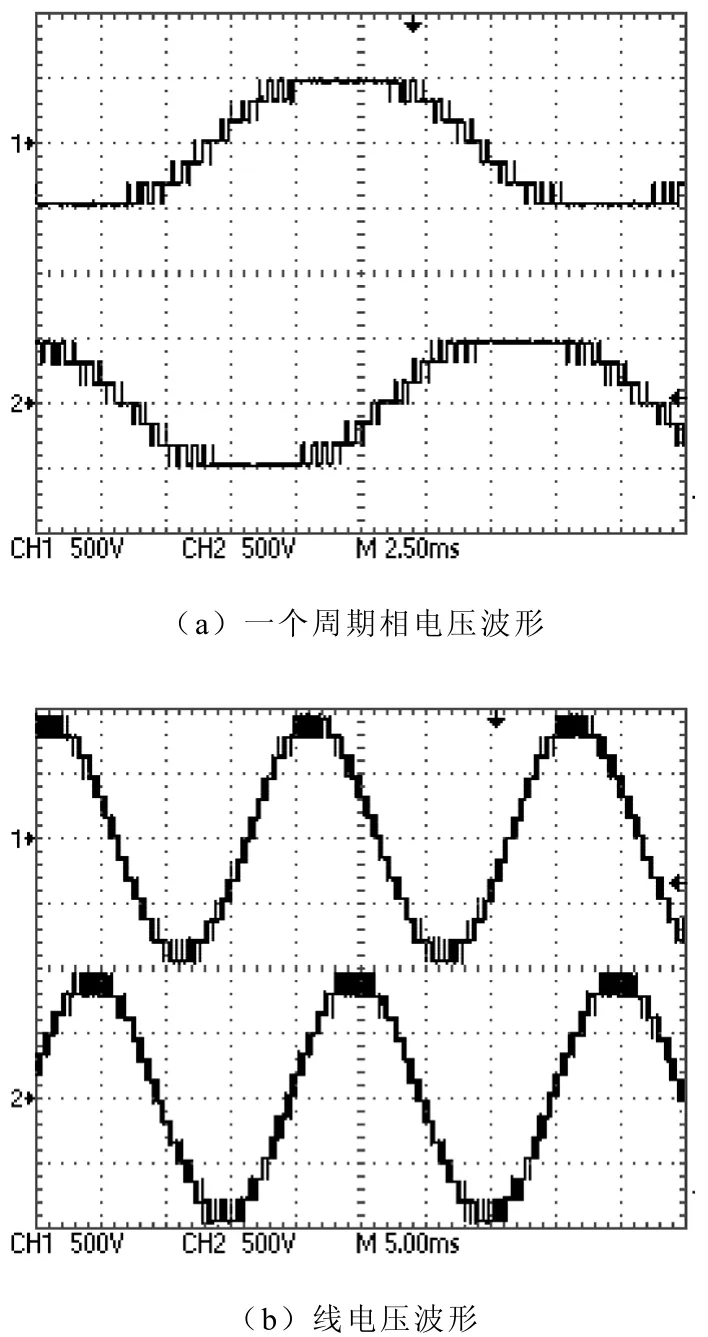
图5 开关频率优化算法实验波形Fig.5 Experimental waveforms of the switch frequency optimized algorithm
为了与现有的调制方法进行比较,采用同相层叠正弦调制算法(PD SPWM)进行仿真,仿真的调制深度和频率调制比分别为0.97和66,图6为仿真输出的波形,a、b、c三相电平一个周期的变化次数依次为 138、138、139,即三相相电压的变化次数为138+138+139=415。图7为同相层叠调制算法的实验波形,图7a是一个周期的相电压波形,从图中可以读出其中两相电压的变化次数分别为 135、138。
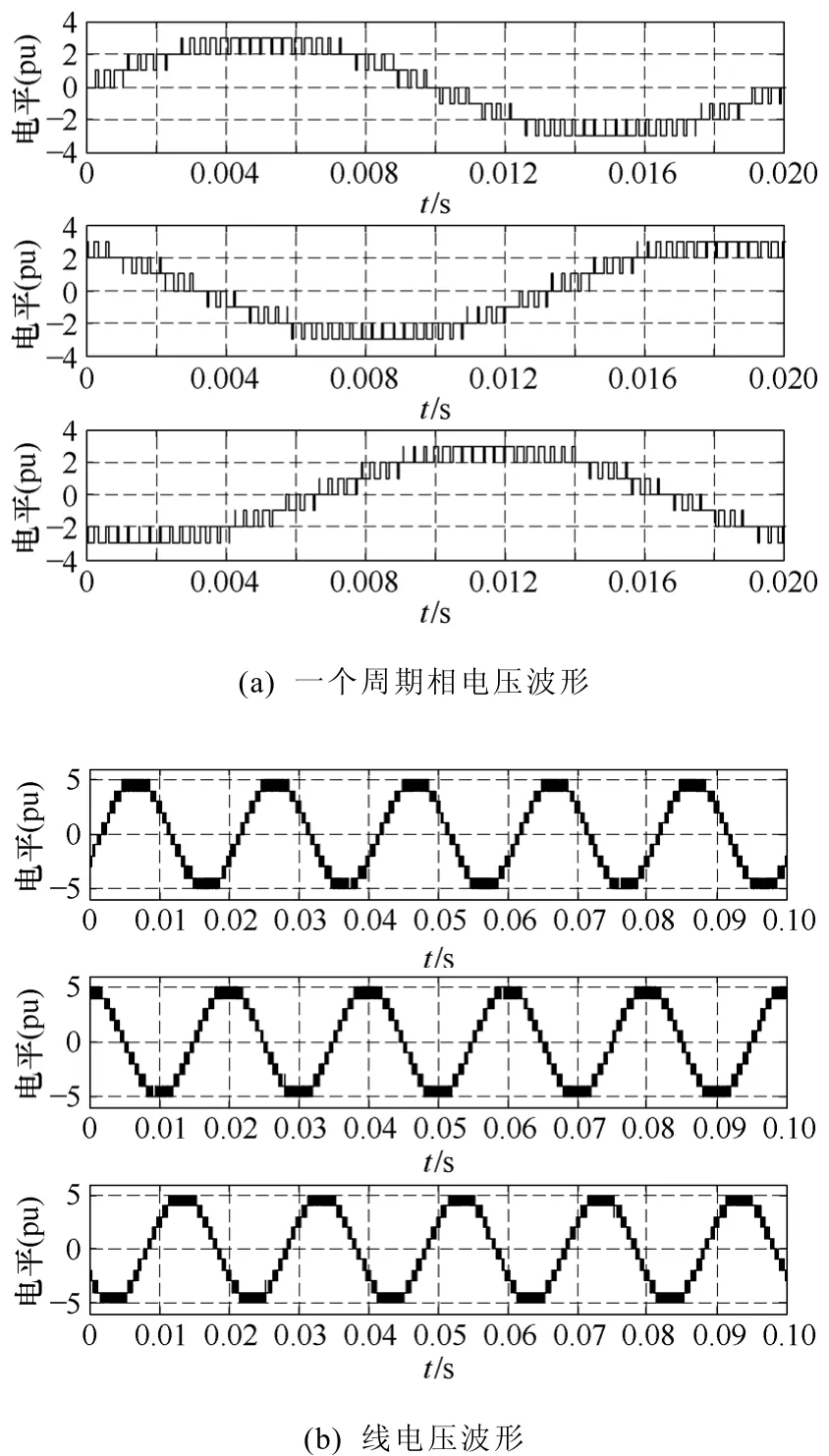
图6 载波同相层叠调制算法仿真波形Fig.6 Simulation waveforms of PD SPWM algorithm
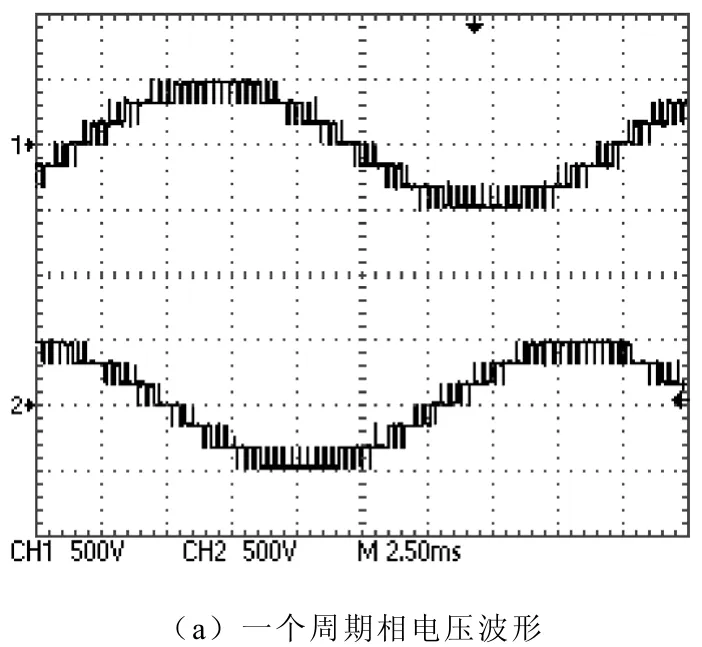
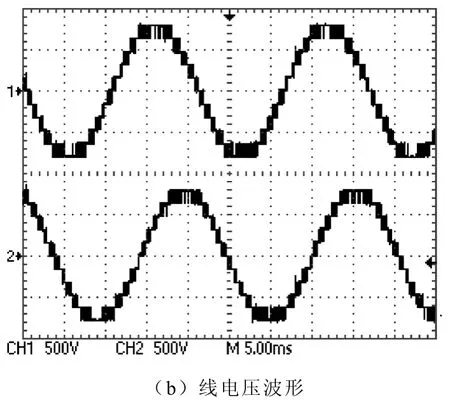
图7 同相层叠正弦调制算法实验波形Fig.7 Experimental waveforms of PD SPWM algorithm
图8为优化开关频率的负载电压实验波形,从图中可以看出,输出电压能很好地跟踪参考电压的变化。

图8 负载相电压波形Fig.8 Phase voltage waveforms of load
7 结论
为了减少开关切换次数,本文利用特征网络和特征四边形的概念,沿着特征四边形的边实现三角形扇区顶点的切换。文章充分研究三级七电平逆变器的特性,针对不同调制系数下得到的特征网络,分别给出开关切换次数的计算方法,并对每种算法的开关切换次数进行了估算。仿真和实验结果与理论推导结果一致,验证了本文提出的算法的正确性和有效性,且输出电压波形能很好地逼近参考电压,与同相层叠正弦调制法的仿真和实验结果相比较,采用本文提出的调制算法,开关切换次数降低到160/415≈38.6%。
[1]Rodriguez Jo Se, Moran Luis, Correa Pablo, et al. A vector control technique for medium voltage multilevel inverters[J]. IEEE Transactions on Industrial Electronics, 2002, 49(4)∶ 882-888.
[2]Rodriguez Jose, Moran Luis, Correa Pablo, et al. A high performance vector control of an 11-level inverter[J]. IEEE Transactions on Industrial Electronics, 2003, 50(1)∶ 80-85.
[3]王群京, 陈权, 姜卫东, 等. 一种降低三电平逆变器开关损耗的PWM方法[J]. 电气传动, 2007, 37(3)∶26-29.Wang Qunjing, Chen Quan, Jiang Weidong, et al.PWM method for reduction of switching loss in 3-level inverter[J]. Electric Drive, 2007, 37(3)∶ 26-29.
[4]张杰, 邹云屏, 张贤. 基于 TMS320F240的三电平逆变器 SVPWM 实现[J]. 通信电源技术, 2003, 2∶10-13.Zhang Jie, Zou Yunping, Zhang Xian. Realization of three-level SVPWM inverter based on TMS320F240[J].Telecom Power Technologies, 2003, 2∶ 10-13.
[5]王鸿雁, 邓焰, 赵荣祥, 等. 飞跨电容多电平逆变器开关损耗最小PWM方法[J]. 中国电机工程学报,2004, 24(8)∶ 51-55.Wang Hongyan, Deng Yan, Zhao Rongxiang, et al.Switching loss minimizing PWM method for flying capacitor multilevel inverter[J], Proceedings of the CSEE, 2004, 24(8)∶ 51-55.
[6]周京华, 沈传文, 苏彦民. 多电平逆变器不连续空间矢量调制策略的研究[J]. 电力电子技术, 2005,39(5)∶ 15-17.Zhou Jinghua, Shen Chuanwen, Su Yanmin. Research on multi-level inverter discontinuous space vector modulation strategies[J]. Power Electronics, 2005,39(5)∶ 15-17.
[7]阎治安, 唐明, 易萍虎. 电机控制中电压空间矢量脉宽调制算法的探究[J]. 西安交通大学学报, 2006,40(12)∶ 1374-1377.Yan Zhian, Tang Ming, Yi Pinghu. Space vector pulse width modulation algorithm with applications[J].Journal of Xi'an Jiaotong University, 2006, 40(12)∶1374-1377.
[8]马丰民, 吴正国, 张志强. 基于小开关损耗的随机脉宽调制技术[J]. 电机与控制应用, 2006, 33(11)∶18-21.Ma Fengmin, Wu Zhengguo, Zhang Zhiqiang.Random PWM technique based on small switch losses[J]. Electric Machines & Control Application,2006, 33(11)∶ 18-21.
[9]唐雄民, 龚理专, 彭永进. 一种快速的多电平空间矢量调制算法研究[J]. 高电压技术, 2006, 32(2)∶75-77.Tang Xiongming, Gong Lizhuan, Peng Yongjin. New fast algorithm for vector control of multilevel inverter[J]. High Voltage Engineering, 2006, 32(2)∶75-77.
[10]宋文祥, 陈国呈, 武慧, 等. 一种具有中点电位平衡功能的三电平空间矢量调制方法及其实现[J]. 中国电机工程学报, 2006, 26(12)∶ 95-100.Song Wenxiang, Chen Guocheng, Wu hui, et al. A novel SVPWM strategy and its implementation considering neutral-point potential balancing for three-level NPC inverter[J]. Proceedings of the CSEE,2006, 26(12)∶ 95-100.
[11]宋文祥, 陈国呈, 束满堂等. 中点箝位式三电平逆变器空间矢量调制及其中点控制研究[J]. 中国电机工程学报, 2006, 26(5)∶ 105-109.Song Wenxiang, Chen Guocheng, Shu Mantang, et al.Research on SVPWM method and its neutral-pointpotential control for three-level neutral-point-clamped(NPC)inverter[J]. Proceedings of the CSEE, 2006,26(5)∶ 105-109.
[12]刘铮, 王翠, 彭永进.优化开关频率的空间矢量调制算法[J]. 高电压技术, 2008, 34(6)∶ 22-27.Liu Zheng, Wang Cui, Peng Yongjin. Optimized switching frequency SVPWM algorithm[J]. High Voltage Engineering, 2008, 34(6)∶ 22-27.
[13]王翠, 刘铮, 彭永进. 一种快速的多电平空间矢量调制算法[J]. 高电压技术, 2009, 35(6)∶ 1445-1450.Wang Cui, Liu Zheng, Peng Yongjin. Fast algorithm for space vector modulation of multilevel inverter[J].High Voltage Engineering, 2009, 35(6)∶ 1445-1450.

