基于差分进化算法的枞树型叶根测量数据处理方法

巫志华 范小平

（东方汽轮机有限公司，四川 德阳，618000）

0 引言

透平叶片叶根的形式对叶片的整体强度振动特性有很大的影响。枞树形叶根以其良好的承载特性和强度适应性而在燃气轮机及蒸汽轮机叶片设计中得到广泛的应用，尤其是在负荷较高，载荷比较复杂的透平级中，如透平末级，这类叶根的应用就更为普遍，但其尺寸精度要求比较高。在叶片的强度振动分析中，首先需要得到包括叶根在内的叶片型线数据，实际上，在很多情况下，原始的设计型线数据是无法得到的，如对进口原装机组叶片的力学性能分析，这就需要采用一定的方法进行测绘处理得到型线后才能进行相应的分析。由于枞树型叶根的型线相对比较复杂，测量数据相对比较多，采用的数据处理方法对在同一精度范围内的测量数据进行合理的处理将对分析结果的可信度有直接的影响。

已有大量的文献和专著对测量数据处理的理论与方法进行了研究和分析［1］。测量数据的处理在数学上通常表述为最优问题的求解。本文针对某一大功率汽轮机末级动叶的测绘，对该动叶的五齿枞树型叶根测量数据进行处理，结合枞树型叶根的结构特点，建立了一种合理的最优问题求解模型，并采用差分进化算法进行求解，以解决此类叶根测量数据的处理问题。

1 枞树型叶根测量数据处理的数学模型

1.1 枞树型叶根的结构特点

图1是一种典型的五齿枞树型叶根母线形式，也是本文测绘的叶根所采用的结构形式，实际的叶根由母线通过旋转或者沿指定方向的轴线延伸就可以得到。叶根母线上每个工作齿，由工作面、非工作面及由工作面到非工作面的过渡结构组成。工作面和非工作面通常由直线组成，而过渡结构则采用圆弧—直线—圆弧连接，实际上，过渡结构也可以采用其他的形式。出于对力学性能要求的保证，在枞树型叶根的设计和制造中，对工作面的加工要求要比非工作面的严格，而且工作面间的公差尺寸及间隙控制是非常严格的，这也意味着从测量数据在工作面的倾角及节距的一致性方面能够反映出测量的准确程度。本文所用到的测绘数据中，反映工作面特征的数据的一致性就非常好，因此可以采用简单的方法就确定了工作面的倾角和节距。以下的数学模型中就把工作面的倾角和节距作为约束条件进行处理的。

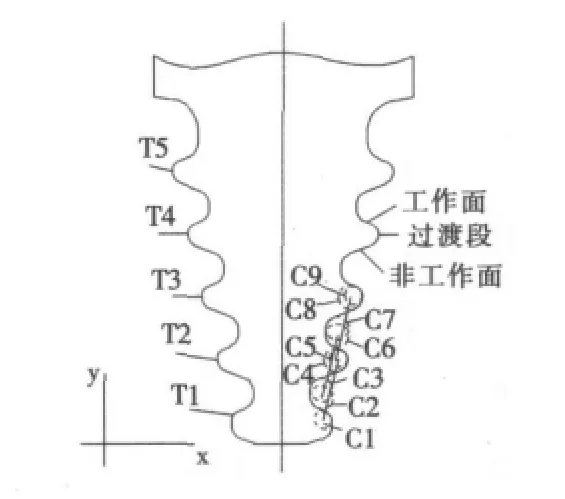
图1 五齿枞树型叶根型线图

1.2 数学模型的建立

对叶根的测量是在三坐标测量仪上实现的，在固定z坐标条件下，对母线轴线进行测量得到一数据集合，该集合由119组 （x,y）坐标点组成，因此，型线可以用y=f（x）的函数形式来描述。

从测量的数据特点来看，我们初步可以确定过渡结构是采用圆弧—直线—圆弧连接的，过渡段与工作面或者非工作面间均是相切的关系，结合枞树型叶根的结构设计特点，我们可以定义图1中的各圆之间的几何相关关系。即在理论设计型线中，T1，T2，T3，T4，T5各齿的工作面是完全一样的，T1齿与其余各齿的非工作面略有区别。C1、C5、C9表示的圆半径相同，而且C1圆心到C5圆心的距离与C5到C9圆心的距离相等，正好等于一个节距，其他的圆也有同样的关系。此外，C1与C2圆相切的角度就是工作面的倾角θ1。因此，设定C1圆心为 （x1，y1）， 半径为 r1， C2圆心为 （x2，y2），半径为 r2， C3圆心坐标为 （x3，y3）， 半径为 r3， C4的半径为 r4， 圆心为 （x4，y4）， C3和 C4外切线的倾角等于非工作面的倾角θ2，可见，母线的基本型线就可以由上述12个自由参数定义。根据测量数据的特点，我们可以将测量数据映射到由这12个自由参数定义曲线上的相应位置上。这样，要求解这12个参数，我们就可以转化为数学上的一个最小值求解问题，即：测量点偏离由该12个自由参数定义的曲线的距离最小。数学表述为：

定义点到直线的距离为Dis1，定义点到圆心的距离为Dis，点偏离圆弧的距离定义为Dis2=｜Dis-r｜，若认为该点在弧线上的，则Dis1i=0，若认为该点在直线上的，则认为Dis2i=0，则

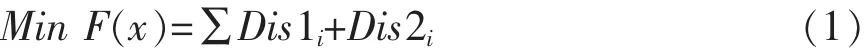
优化变量为上述12个参数，同时根据设计经验，各r及θ2需要圆整。

在实际的优化过程中，我们分两次进行优化，第一次对r和θ2无圆整约束，根据计算结果，对r和θ2进行圆整处理进行约束后进行第二次优化。

2 差分进化算法 （DE）用于枞树型叶根测量数据处理

进 化 算 法 （Evolutionary algorithms， 简 称EAs），是模拟自然界的进化和遗传现象而提出的一类随机优化算法，这类算法已广泛应用于各种优化问题的求解。由Storn和Price为求解Cheby-shev多项式而提出的差分进化算法 （Differential evolution，简称DE）[2]因其原理简单、受控参数少、算法结构紧凑、操作简便，鲁棒性强和优秀的全局寻优能力，已成为最好的进化算法之一。

在DE算法中，通过差分算子，利用种群中多个个体的信息计算新个体，在完成对新个体适应度的评价后进行选择操作生成新的种群。用表示第t代中第i个染色体：

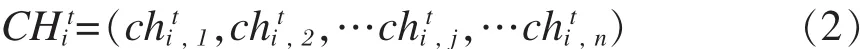
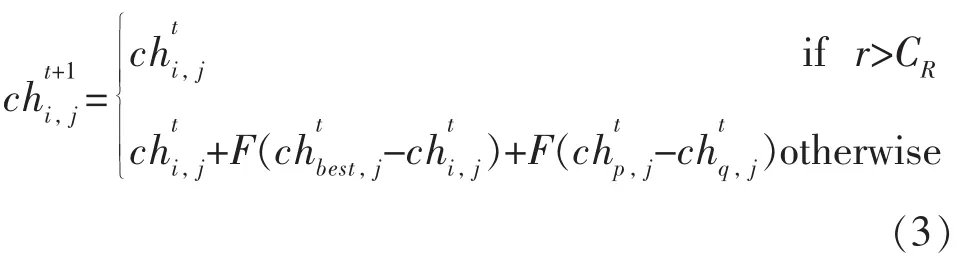
可见在差分算子中只涉及两个控制参数：变异算子 F和交叉算子 CR。其中 F， CR∈ ［0，1.0］，本文分别取0.7和0.5。r是 ［0，1.0］之间的随机数。

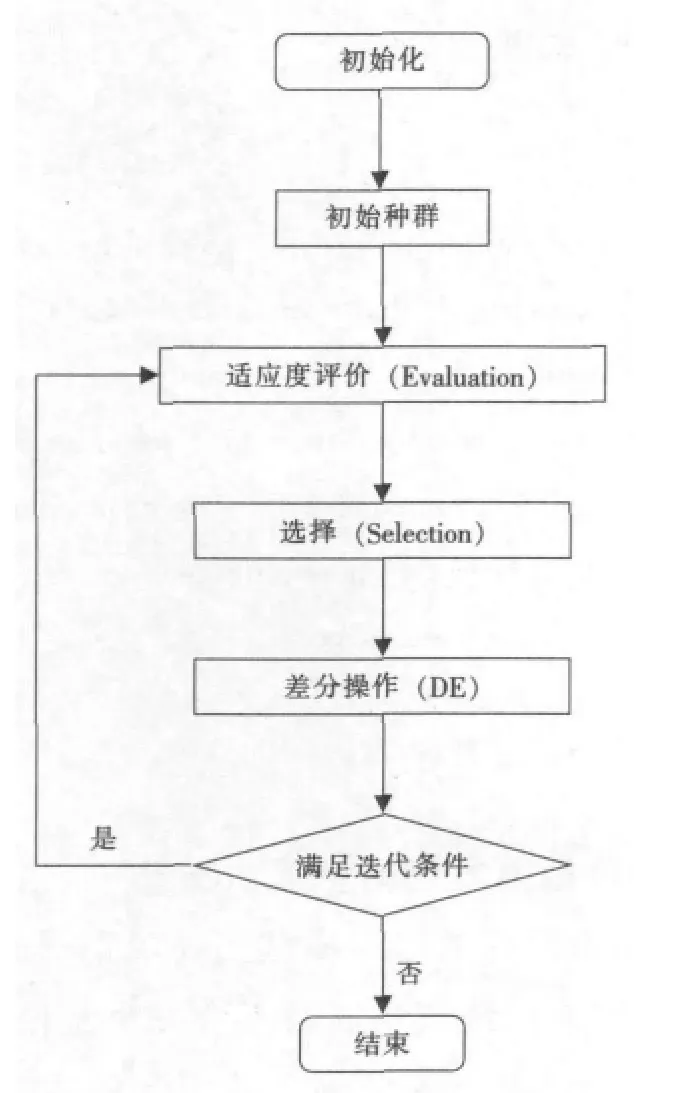
图2 DE算法流程图

为了测试DE算法和计算程序的有效性，本文采用如下的函数来做测试：

图3 函数y=f(x)的曲线图

图3是该函数在约束区域内的变化曲线，从图上可以发现，在该约束区域内出现多个极值，能很好的反映算法的寻优能力。设种群数为50，最大迭代步数为100，在20步左右就达到最小值0.049740，与该函数在这一范围内的理论最小值相差无几，可以作为问题的全局最优解。可见，DE算法的寻优能力是令人满意的。

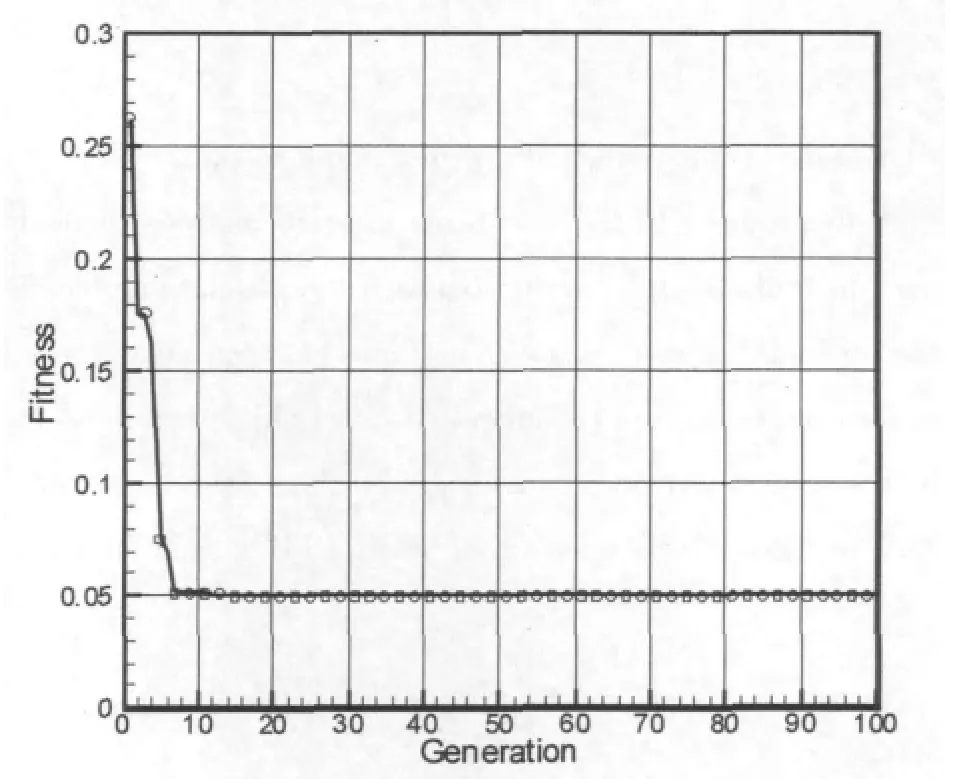
图4 适应度曲线

采用DE方法，对上述枞树型叶根的12个参数进行求解，设种群数为80，最大迭代步数为2000，对12个参数的搜索范围的定义可以先根据原始测绘数据预估一个相对大的范围，反复多次，最终优化结果是一致的。从图5的结果来看，计算结果是合理的。

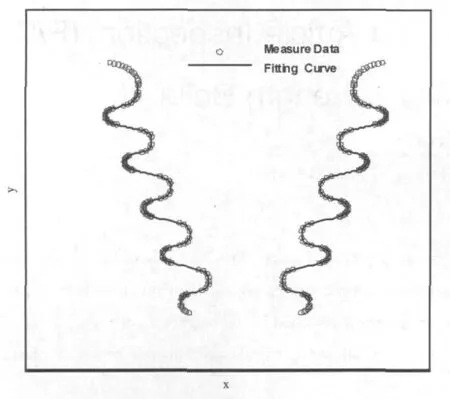
图5 枞树型叶根拟合曲线图

3 结论

本文结合枞树型叶根的型线特点，将枞树型叶根测量数据逆向工程问题转化成最优问题，并采用差分进化算法进行求解，计算结果表明：这一处理模式是合理的，这种模式同样适用于其他形式的叶根测量数据处理;差分进化算法很适合多约束条件下多参数的寻优求解问题。

[1]刘大杰,陶本藻,主编.实用测量数据处理方法.北京：测绘出版社,2000

[2]Storn R.On the usage of differential evolution for function optimization [A].BiennialConference of the North American Fuzzy Information Processing Society [C].1996.519-523

[3]宋立明.基于进化算法的轴流式叶轮机械叶栅气动优化设计的研究 [D].西安交通大学博士学位论文，2006