风电叶片疲劳试验载荷确定方法研究

黄志华 黄永东 赵 萍 钟贤和

（东方汽轮机有限公司，四川 德阳， 618000）

0 前言

风电叶片作为风力机的重要组成部件，在风场的实际运行中承受着不断变化的风载荷作用，恶劣的气候环境和叶片长年累月的不断运行，使得风电叶片的疲劳寿命备受人们关注。为检验风电叶片的疲劳使用寿命是否能达到设计要求，国外学者和专家已做过大量的工作。相比之下，国内在这方面的研究和试验相对较少。

通常风电叶片的认证试验分为静力试验认证和疲劳试验认证两方面，静力试验认证主要检验叶片的质量、固有频率、极限载荷下的强度极限和稳定性是否满足设计要求，而疲劳试验则检验叶片的结构、铺层和粘接设计是否合理，是否能达到预设计的叶片使用年限，同时也可发现在叶片生产制造过程中的一些制造缺陷。

根据国外已进行的试验和经验，风电叶片的疲劳试验主要分为双轴和单轴疲劳加载试验，双轴加载疲劳试验可同时进行挥舞和摆振两个方向的试验，单轴加载试验则每次只进行挥舞或摆振方向的试验，可见前者比后者对叶片的检验更加节省时间和节省相应的试验费用，但试验设备要求更高、试验难度更大。结合国内自身条件以及中国船级社叶片疲劳试验规范的要求，此次叶片的疲劳试验只进行挥舞方向的疲劳试验。本文就DF64A风电叶片进行的单点单轴恒幅值加载方式下的疲劳试验进行疲劳试验载荷设计方法研究。

1 疲劳试验的目的及试验载荷确定原则

叶片在实际运行中疲劳载荷谱非常复杂，图1（以My为例）仅是一个截面的疲劳载荷谱，每个截面疲劳载荷谱不同，同时同一个截面振幅都在不断变化且振动次数非常多 （20年的寿命内），无法模拟，因此必须采用简化加速方法在较短的时间内等效模拟叶片的实际运行情况，检验试验叶片是否能够安全运行。即对叶片仅施加疲劳载荷My，所加载荷的等效损伤与叶片运行寿命内的等效损伤相同，检验叶片在试验中是否破坏。

图1 DF64A某截面My实际的疲劳载荷谱

1.1 关注截面位置

因为疲劳试验仅能在局部加载，仅能关注一个截面，根据疲劳强度分析，选取疲劳安全裕度最小的截面作为疲劳试验验证截面。

1.2 试验次数的选取

为了使叶片的试验时间不能太长，也避免由于次数太少导致试验不能反映真实情况，一般确定试验次数为 Ns=5×106～1×107次 （根据船级社规范要求），试验的频率与叶片一阶挥舞频率相近，在该频率之下进行疲劳载荷的激振试验，这样在最长3～4个月就能够完成叶片疲劳试验。

1.3 疲劳载荷计算的关注点

将损伤最大的位置作为疲劳计算的关注点。为了便于计算与测试之间的相互关联，取损伤最大截面的叶片外层应变为疲劳计算的关注点，以便与测试结果对比，另外，通过有限元的计算可以分析外层应变与其他各层应变之间的差异。

2 叶片的疲劳损伤计算

2.1 叶片的有限元模型

图2 DF64A风电叶片有限元模型

建立DF64A叶片疲劳损伤计算的叶片有限元模型，有限元网格划分如图2所示。最终的计算模型需要对叶片有限元模型进行复合材料铺层，并在叶根处施加固定支撑约束模拟叶片的工作状况。

2.2 计算叶片的疲劳损伤最大作用系数

在叶尖施加挥舞、摆振和轴向三个方向的单位载荷，利用MSC.Patran软件计算出叶片有限元模型各个截面的应变值，引入Bladed软件计算得出的疲劳载荷谱 （即Markov矩阵）计算得到疲劳载荷作用下叶片各截面的应变值，利用玻璃纤维复合材料疲劳损伤的计算理论，运用自编的Matlab软件计算并绘制出叶片各截面疲劳损伤的最大作用系数 （见图3）。

图3 DF64A风电叶片疲劳损伤的最大作用系数

从图3中可以看出，叶片13.5m截面主梁帽部分最容易产生疲劳破坏，根据叶片疲劳损伤的计算结果结合叶片13.5m截面的有限元网格，可进一步确定出叶片最易疲劳损坏的位置为13.5m截面吸力侧主梁帽中心位置靠近后缘100mm处的最外层纤维方向，于是可确定该位置为叶片疲劳试验危险截面的危险点 （定义为疲劳载荷设计点），同时将该位置最外层的纤维方向应变作为设计疲劳试验载荷基准值。

由于本次疲劳试验采用单点单轴的加载试验方式进行挥舞方向试验，所以在确定疲劳载荷设计点之后，还需计算叶片在单位弯矩My作用下，该点的纤维方向应变值，以便进行疲劳载荷设计。

3 计算疲劳试验载荷

3.1 计算疲劳载荷设计点的疲劳损伤

使用有限元软件MSC.Patran计算出在单位弯矩My作用下，疲劳载荷设计点的应变值εf（纤维方向），见表1。

表1 单位弯矩下疲劳载荷设计点的应变

表2为叶片13.5m截面疲劳载荷My作用下的 Markov矩阵。

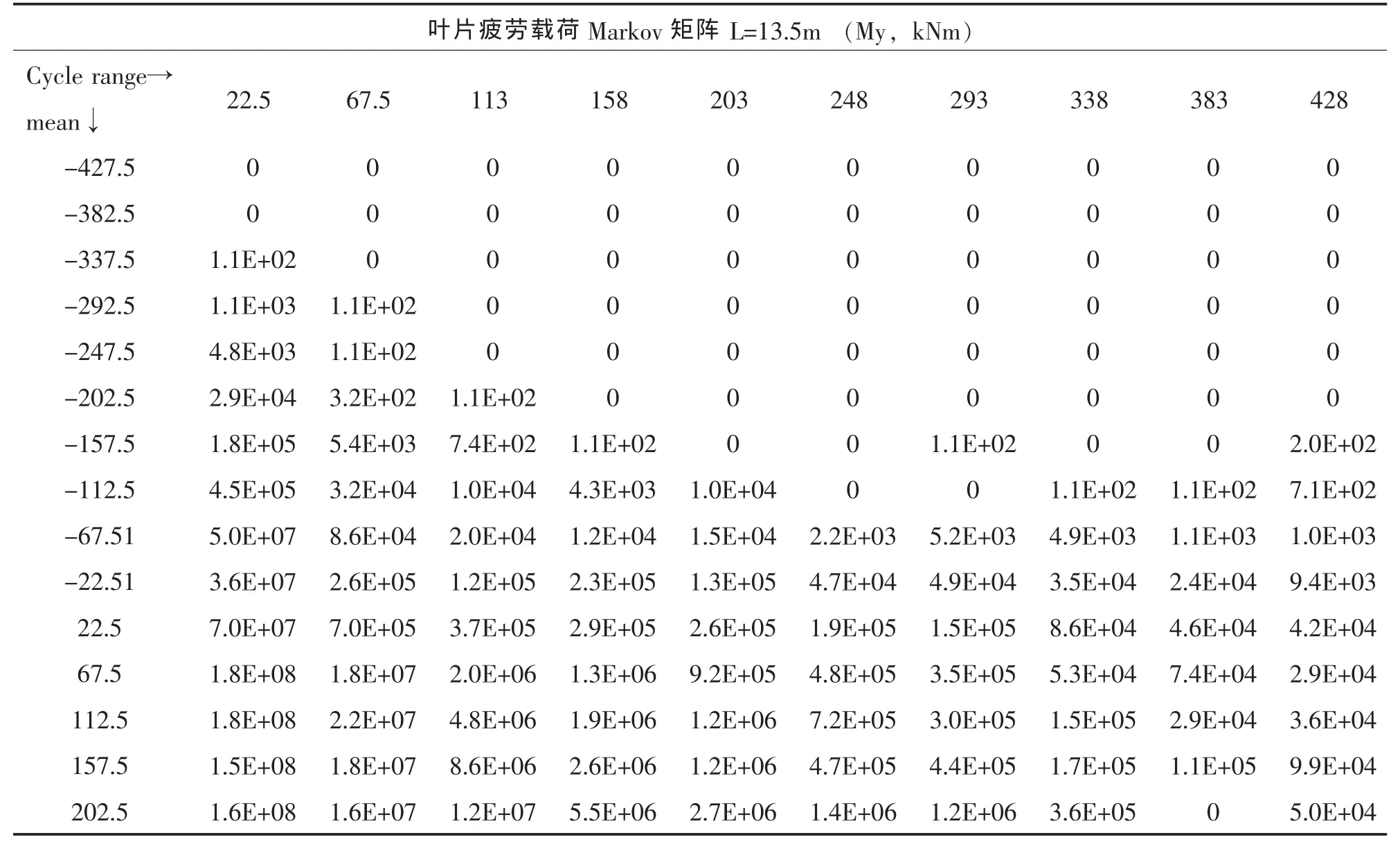
表2 13.5m截面疲劳载荷My作用下的Markov矩阵 （部分）

将计算出的单位载荷下的应变值乘上载荷幅值得到相应循环载荷作用下的应变动态幅值SK，A，再将单位载荷下的应变值乘上载荷均值得到循环载荷作用下的应变均值SK，M。利用玻璃纤维复合材料疲劳寿命计算公式，可以得到疲劳载荷设计点在疲劳载荷My作用下的疲劳寿命次数N：

式（1）中：

Rk，t—特征短期结构元件的拉伸强度；

Rk，c—特征短期结构元件的压缩强度；

γMa—材料的局部安全系数 （静强度）；

γMb—材料的局部安全系数 （疲劳强度）；

Clb=N1/m；

m—S-N曲线的斜率参数。

式（1）中各参数在计算中取值如表3所示，其中DF64A叶片为聚酯树脂基体，所以m取值为9。

表3 疲劳寿命计算使用数据

确定出叶片的疲劳寿命次数后，则可根据Miner线性损伤理论计算得到疲劳载荷设计点的疲劳损伤D值：

其中：ni—实际某个循环次数；

Ni—某个循环的疲劳寿命次数：

体育小镇的空间布局受居民体育旅游需求以及体育旅游资源的吸引定向性等主客观因素的影响[8]。因此，体育小镇的空间布局需要考虑居民体育旅游的多样性偏好、出游半径以及出游成本等方面的因素，在空间布局过程中，应避免某一区域同类型体育小镇的重复建设，从异质性的角度出发，差异化布局，实现体育小镇优势互补。以环太湖体育圈为例，作为体育小镇空间布局的轴线，环太湖体育旅游资源有一定的相似性，在后续体育小镇的建设中，应发挥地域特色优势，如苏州渔洋山飞行伞训练基地、宜兴湖父镇竹海风景区等可依据特色体育项目开展体育小镇建设。

D—叶片在给定Markov矩阵载荷作用下的损伤。

由此计算出疲劳载荷设计点的疲劳损伤为D=5.14E-2。

3.2 计算恒幅值疲劳载荷下的应变均值和幅值

由于实际叶片在风场运行时，其疲劳载荷为变幅载荷谱，而实际试验过程中所施加的疲劳载荷为等效的恒幅值疲劳载荷，因此，需要将各个工况下的变幅疲劳载荷转换成恒幅值的单点单轴疲劳加载方式。

由疲劳损伤理论可以知道，应变均值SK，M和应变幅值SK，A之间具有一定的比例关系，其数学公式可以用式（3）来表示：

式（3）中：R 表示载荷比 （R=SK，Min/SK，Max）， 即某个载荷循环的最小应变与最大应变的比值。考虑疲劳试验中其配重为600kg和叶片自重的情况下，R取值为-0.54132。

再根据式（4）可计算出相应恒幅疲劳载荷下叶片的应变均值，同时利用式（3）可一并计算出等幅疲劳载荷下的应变幅值，具体数值见表4所示。

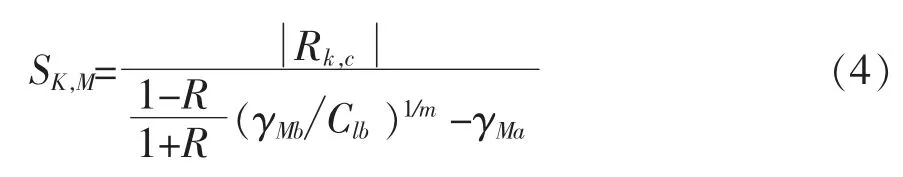
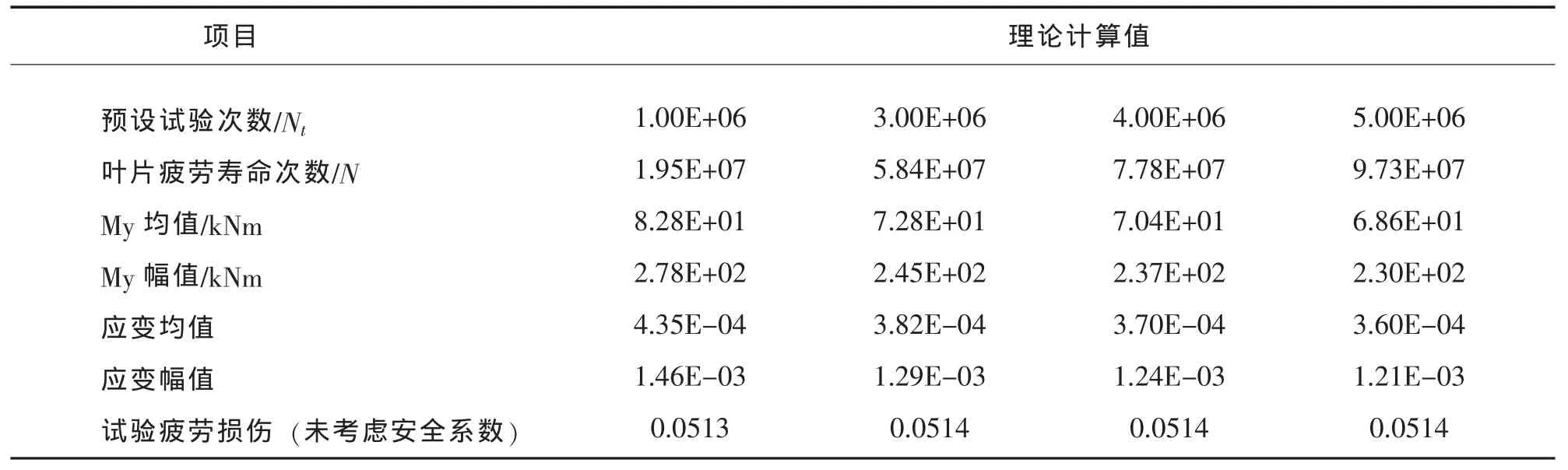
表4 各预设试验次数疲劳载荷设计点的应变均值和幅值

3.3 计算疲劳试验的试验 （激振）载荷

由疲劳理论分析可知，疲劳载荷设计点的应变均值由叶片自重和配重产生，应变动态幅值由作用在叶片上的动态激振力产生。所以根据此对应关系，可进一步确定出疲劳试验时作用在叶片上的动态激振力。

考虑到叶片之间的分散系数和疲劳计算公式的不确定性，实际计算疲劳试验载荷时，需考虑上1.155的疲劳试验载荷系数 （见表5）。

表5 疲劳试验载荷系数

根据试验规范的要求和该叶片疲劳危险截面的位置，以及减少疲劳试验时间的目的，最终将叶片截断为23m，并选择疲劳试验载荷的加载位置在叶片的21m截面，此时计算出的激振力静态幅值和配重见表6所示。

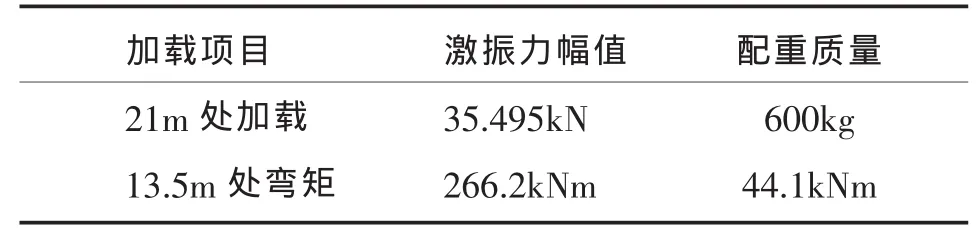
表6 疲劳试验静态加载参数

4 静态载荷的有限元验证

将上面计算得到的静态数据与试验有限元方法计算出的数据进行对比，以确定利用上述理论计算的正确性。按挥舞正方向和挥舞负方向两种工况，将上面得到的疲劳试验静态加载参数输入到1.0MW叶片的有限元模型里进行计算，则得到的疲劳载荷设计点的应变值见图4所示。

表7给出了根据疲劳理论计算出的疲劳载荷设计点应变值和有限元计算值之间的对比。

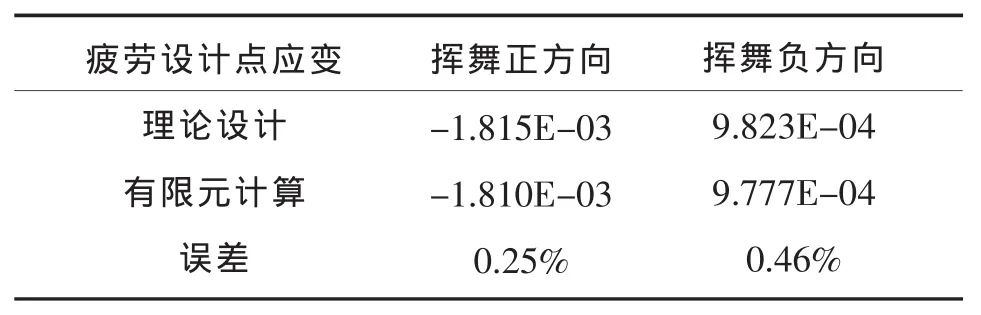
表7 理论设计值与有限元计算值对比

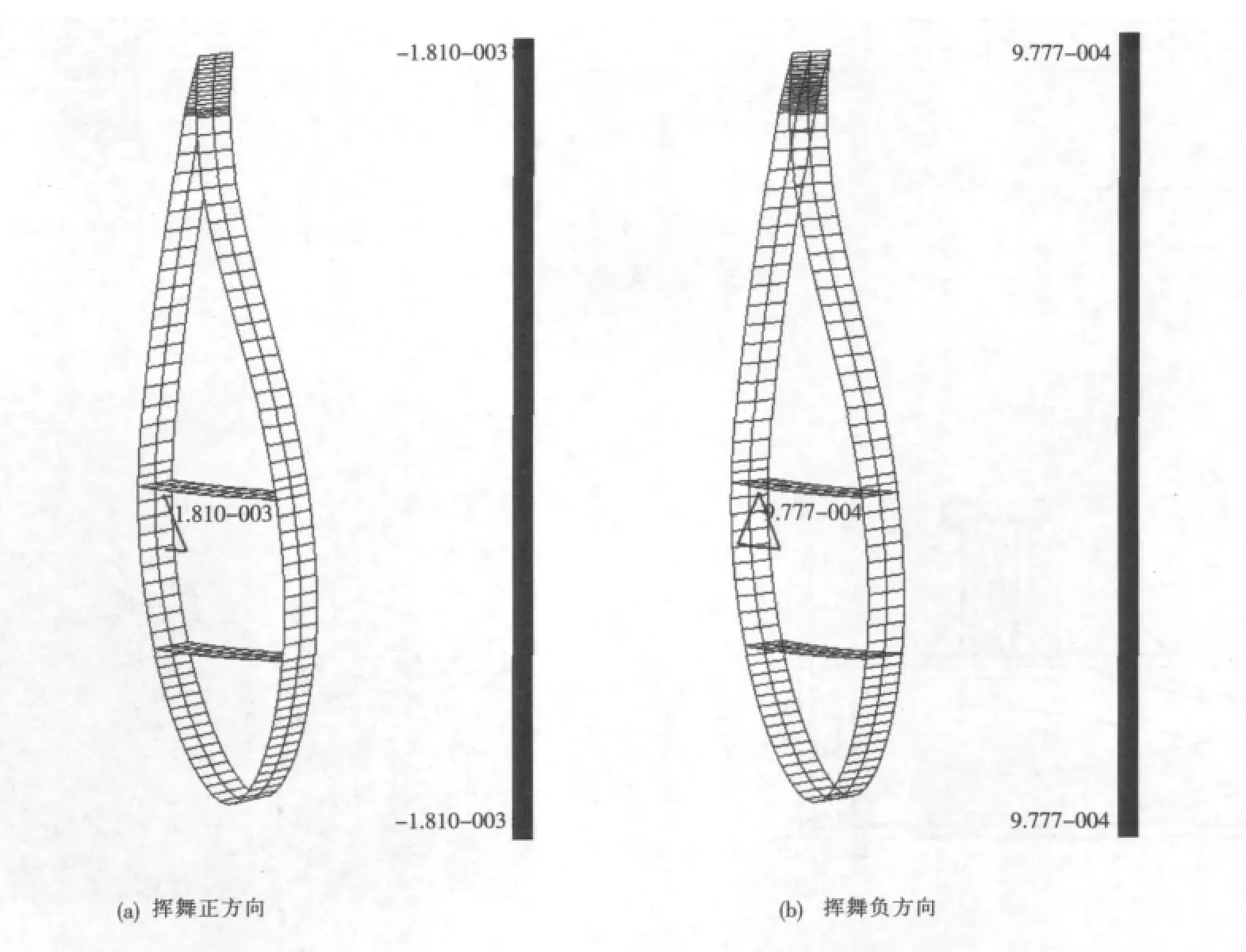
图4 有限元模型静态加载时疲劳设计点的应变值

根据表7的对比结果可以知道疲劳理论计算得到的疲劳试验载荷应变值是合理的。

5 疲劳试验的动态加载载荷

由于风电叶片在疲劳试验中是一个往复振动，即叶片在疲劳试验过程是进行动力学运动的。为了在疲劳试验中尽量增大疲劳载荷的动态激振力，为此，在疲劳试验过程中，其疲劳载荷的激振频率则必须运行在叶片挥舞方向1阶固有频率附近，因此，此时需要考虑叶片疲劳动力模型的动力学放大效应，经过反复的动力学模型有限元计算分析，最终确定疲劳试验动态加载载荷如表8所示，表9是在相应疲劳试验载荷下的疲劳损伤值。

表8 疲劳试验动态加载载荷

表9 疲劳载荷设计点损伤和应变计算值

根据等效疲劳损伤原理，设计出如图5～图6的试验装置图，图7是试验的实景。

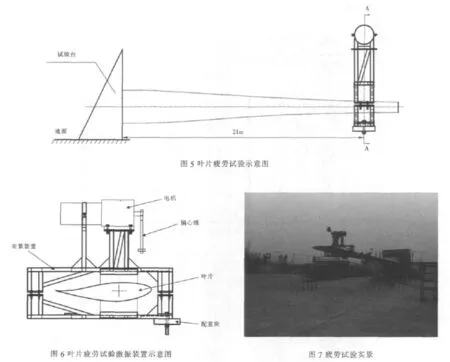
根据该试验载荷的设计结果，在3个月可完成5.00E+06次的叶片疲劳试验。该实验已经完成并通过船级社的见证。

6 结论

本文针对1.0MW风电叶片DF64A疲劳试验，按照IEC规范和中国船级社的要求，按单点单轴恒幅值加载方式的要求，采用疲劳理论计算和有限元软件计算相结合的方法，设计出了该DF64A风电叶片疲劳试验时的疲劳动态加载载荷 （包括激振频率、加载幅值、配置质量等），阐述了风电叶片在单点单轴恒幅值加载方式下，疲劳试验载荷的一种设计思路和方法，可以在较短的时间之内模拟叶片的实际运行情况，为风电叶片的疲劳试验奠定了一定基础。

[1]International Electrotechnical Commission88/102/CD.Draft IEC 61400-22：Wind Turbine Certification.December 1998

[2]International Electrotechnical Commission88/84/CD.Draft IEC 61400-23：Testing of Rotor Blades.September 1998

[3]Hughes,S.Musial,W.And Stensland,T.Implementation of A Two-Axis Servo-Hydraulic System for Full-Scale Fatigue Testing of Wind Turbine Blades.NREL/CP-500-26896.Windpower 99 Proceedings;June 20-23,1999,Burlington,Vermont.Washington D.C.：American Wind Energy Association

[4]Larwood,S.and Musial.W.D.,Comprehensive Testing of Ned Wind 12 Meter Wind Turbine Blades at NREL.Proceedings 39th AIAA Aerospace Sciences Meeting,Wind Energy Symposium,Reno,Nevada,January 2000

[5]刘万坤,等.风能与风力发电技术.北京：化学工业出版社，2006.9