区域货物综合运输网络容量可靠性分析

郑长江，高正平

(河海大学 土木与交通学院，江苏 南京 210098)*

0 引言

随着经济社会和科学技术的不断发展，可靠性技术已渗入到各个领域，但在交通领域的可靠性研究尚处于起步阶段，只是近几年才开始受到专家与学者的重视，并逐渐成为交通领域研究的一个热点话题.可靠的交通运输网络是区域、城市、城乡内外联系重要的生命线系统(交通运输系统、供水系统、能源供应系统和通信系统等)之一，如果一旦发生破坏事件，不能及时对其进行修复，不仅会增加系统的维修成本和费用，而且会造成巨大的间接费用.为了提供(或获得)可靠、安全、稳定、高效的交通运输服务，管理者和用户越发关注运输系统的可靠性问题.

本文构建综合货物运输网络容量可靠性分析总体框架，将有助于分析货物运输网络单元容量(或通行能力)、运输工具等供给方的变动(如由于事故、天气、灾害等原因导致供给能力的降低等)，或费用、行程时间、行程时间可靠性、枢纽处转换费用、时间及转换时间可靠性、外部成本(如环境污染、能源消耗、土地紧张等)等用户出行方式或路径选择等变化导致的需求变动对整个货运系统可靠性的影响问题，有助于分析资金、土地等有限资源在不同运输方式间如何合理分配，从而为相关部门的规划、建设、运营和组织管理等提供决策依据和技术支撑.

1 综合货运系统的构成

从运输方式组成情况看，综合货物运输系统主要由公路、铁路、水路、航空和管道五种运输方式构成，而从参与综合货运系统运转的诸多要素看，经过归类整理和分析后综合货物运输系统则可看作由用户(Customers)、运营(Operation)、运输工具(Vehicles)、基础设施(Infrastructures)和环境(Environment)构成的一个复杂系统(可以简称为COVIE系统).需要指出的是，不同的参与要素对综合货运系统的正常运转都发挥着积极的作用，而正是不同参与要素的内在功能、相互联系以及和系统容量可靠性之间的关系，形成了分析COVIE系统的基础，包括以下几个方面.

用户(C):可以看成由人或者货组成.正是有了用户的出行需求，才会产生实际的运输量.所有不同用户的出行需求、不同的货种类别，对于出行方式、出行路径选择的结果合成后即形成综合运输网络上的流量模式和状态，因此对于用户行为的分析是整个货运系统容量可靠性研究的一个重要方面.

运营(O):运营指的是运输工具在固定基础设施上的运行情况.由于不同的人或者货物对运输服务的需求不尽相同，这就要求运输工具和其他资源的使用要有针对性，否则会影响到整个运输系统的运转效能.运营包括了提供服务的类型和频率、车辆路径和时刻表、价格机制、联合运营规则等内容.较为典型的系统运营评价指标是服务水平(LOV，Level Of Service).

基础设施(I):指影响综合运输系统容量供给的固件部分，如公路、铁路、机场、港口、物流场站等.由于受交通事故、天气、自然灾害等因素的影响，此类基础设施将丧失部分或全部功能，还会波及至周边的其它基础设施，进而影响整个运输系统的供给能力和系统容量的可靠性.基础设施可靠性与网络系统可靠性的关系一直是国内外研究和关注的重点.

环境(E):狭义的环境一般指自然环境，这里的环境是广义环境，包括自然环境、政治环境、经济环境、社会环境、科技环境等内容，这些都是影响运输系统正常运转的重要因素.如不同的政策将直接影响综合运输系统的供给结构:为了提高土地、能源等资源利用效率，减少环境污染等，发展快速、大容量、低能耗和低污染交通方式的运输政策将直接导致铁路运输和水路运输份额的增长.

2 综合货运网络的描述模型

综合货运网络的描述模型应能反映运输基础设施(含线路和节点)、运输装备、不同货类、OD点对等信息.为了较好的反映网络特征和货物运输情况，包含各种方式的物理网络和枢纽转换节点的一体化运输网络将有助于这一问题的解决.在此借助图论的方法描述综合货运网络.N代表网络中的节点集合，A代表弧或者线段的集合.节点集合反映了所有货物的起点、终点、转换设施、相交路段的交叉口等信息.对OD点对可以做如下定义:起点o∈O⊆N，终点d∈D⊆N，每一个OD点对w=(r，s)，w∈W由多条线段连接而成，用Rw表示.线段是指连接N中两个节点的线路，每个线段a∈A都有其自然属性，如长度、可运行的车辆类型、通行能力、货物流量和费用等.两节点间的平行线段用以表示不同的运输方式，这样既有助于区分同一路径上不同运输方式的货物流，也可以分出不同的服务类型(如快递、平邮等)，甚至还可以根据需要细分出同一运输方式不同的承运人等.

作为综合货运网络实现不同运输方式转换的关键节点，枢纽处的网络描述非常重要.货物在枢纽处进行不同运输方式的转换，必将带来相关的转换费用和延误.参照已有的枢纽表示方法(于世军［1］2006)，并结合本文的研究需要，本文对枢纽中的流量转换作业采用转向弧的形式来建模，称之为联运弧，具体是以转换作业过程中转运前的运输方式弧和转运后的运输方式弧所形成的弧对来表示.如图1所示，当运输对象从一种运输方式的线段a通过枢纽节点转换到另一种运输方式线段b上时，这一过程以联运弧t=(a→b)来表示，弧上允许结合适当的多式联运成本与时间延误函数.

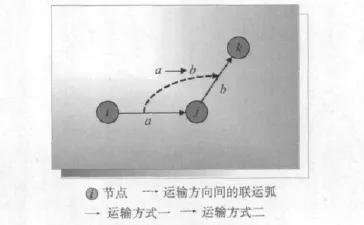
图1 虚拟联运弧示意图

采用这种方法，对于一个三种运输方式相交的运输枢纽，其发生的联运活动可以表示成如图2所示.采用虚拟节点将枢纽节点扩大或分解，再添加上这些虚拟节点之间的虚拟弧，这样形成了对枢纽内联运活动的直观表示.

所选择的这种枢纽表示模型不需要对网络进行大的改动，联运弧由一对实际的运输方式弧来表示，其中一个运输方式弧到达枢纽节点而另一个运输方式弧离开节点.这种联运弧从网络表示的角度可不直接添加到基本网络上，而可以根据枢纽节点上定义联运弧的方式弧对数，通过数据列表的形式来表示.

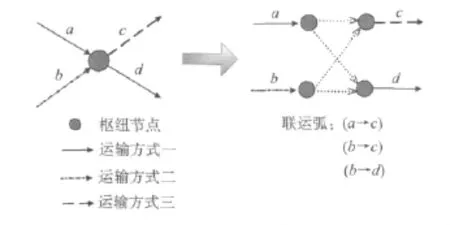
图2 枢纽节点的表示

在定义的基本网络结构的基础上，考虑到对于不同的货物类别，都可以依据该货物的特性由一种特定的运输方式或一组运输方式组合进行运输，因此，可以以基本网络为基础，在模型中创建针对每一种货物类型的子网络.对每一种货物类型k有它自己可利用的子网络，可被定义为代表运输方式的线段集合Ak和转运作业的节点集合Nk，表示如下:

2013年，辽宁省水利厅对省直9座水库工程区率先进行确权划界并封闭隔离。水库工程区的封闭总长度为57.4km，工程所需资金为513.2万元。

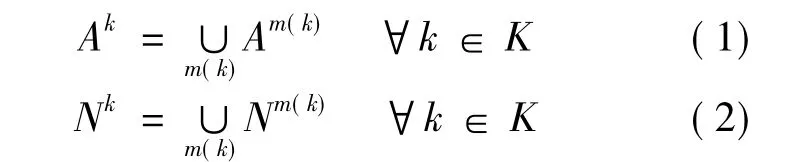
式中，(N，A)是由节点集合N和线段集合A组成的多方式多货类网络，N=和 A=，K为所有货类的集合;M为运输网络上所有可利用的运输方式的集合，M=k)，m(k)为可用于货类k的运输方式的集合，如公路、铁路、航空和(或)水运方式的组合.

3 货运网络容量可靠性分析模型

综合货物运输网络容量可靠性指在一定的服务水平下网络容量满足某一货运需求的概率(chen［2］等 1999，cheng［3］等 2004)，强调的是网络容量与交通需求之间的关系，目前它已成为评价整个网络可靠性的一个较为实用的综合性指标.利用网络保留容量的概念可以较好的分析货运系统可靠性问题.

3.1 网络保留容量

保留容量的概念最早由 Webster和Cobbe［4］(1966)提出，用以分析简单的单个信号灯控制交叉口.Allsop［5］(1972)则运用线控理论将此概念推广至分析更为复杂的信号控制交叉口.Wong和Yang［6］(1997)借助保留容量用以分析和预测路径选择模型下的网络最大容量问题.Chen［2-4］等(1999，2000)在前人研究成果的基础上，认为网络保留容量是将给定的OD需求矩阵分配到网络上而不超过线段通行能力的最大乘子，即在满足网络平衡问题中分配的交通流不超过线段通行能力中这一约束条件下，寻找最大乘子μ，其数学模型表示如下:

式中，xa(μq)是线段 a上的平衡流;ca是线段(弧)的供给能力.式(4)表示所有OD点对之间的需求q被统一放大μ倍.μ可通过下面的网络平衡问题求解.

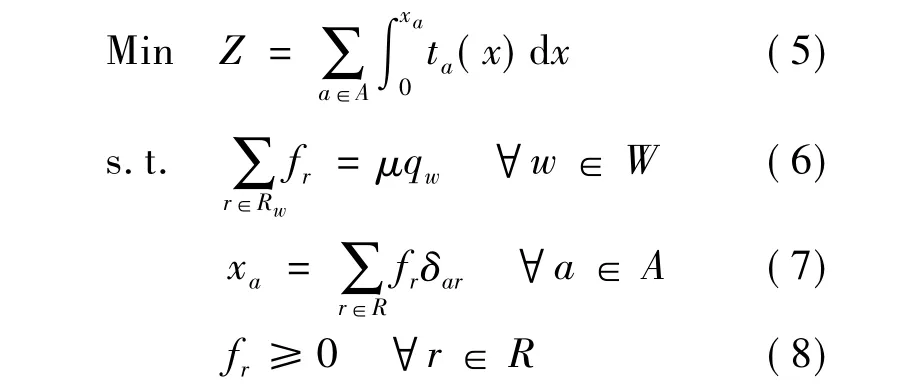
式中，Z是用户平衡方程的目标函数;ta(xa)是线段a∈A上的运行时间;R是整个网络路径的集合;Rw是OD点对w∈W之间的路径集合;qw是OD点对w∈W之间的需求;q是现有OD需求矩阵的向量形式;fr是路径r∈R上的交通流，如果路径r经过线段a，那么δar=1，否则为0.

在此网络平衡模型中，路径选择行为在下层模型中予以体现，而上层规划模型主要求解最大乘子μ.下层规划模型(5)～(8)是一个标准的网络平衡问题，只要根据给定需求扩大μ倍后求解即可.由于上层模型(3)～(4)中只有一个决策变量μ，将其作为下层模型的一个参数，该双层模型即转化为一个单层模型，并且根据平衡流达到线段或节点最大容量这个约束条件来确定μ值.关于更多μ值的分析，可参考chen［2］(1999)的文章.

3.2 货物运输系统不确定因素分析

由于货物运输受经济、社会、环境等外部因素，以及人们对货物运输方式、路径等选择影响，其供给和需求均可能发生变化，以下从基础设施、运输装备、运营水平、环境、用户等五个方面分析货运系统的不确定性.

(1)基础设施(I)因素

影响货物运输系统可靠性的基础设施主要包括线段和节点两个部分.线段基础设施的不确定性主要由交通事故、天气、自然灾害等因素造成，而节点不确定性则由枢纽内部或交叉口处的信号灯控制延误等引起.因此线段流量应小于其最大供给能力，其数学形式表示如下:

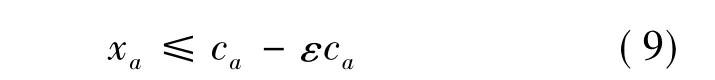
式中，ca是线段a的最大容量，用t表示;ε是确定线段容量变化的参数，变化范围从0(线段通行能力没有任何退化)到1(完全恶化，线段通行能力降为0).ε的概率分布函数p(ε)可以采用实地调查等方法提前获取.

节点流量也应小于节点的最大供给能力，其数学形式表示如下:

式中，gn是节点n内的总流量;In，On⊆A表示分别表示进入和离开节点n的线段集合;cn表示节点n的最大容量，用t表示.

(2)运输装备(V)因素

很显然，OD点对w之间货物总流量不会大于运输工具所提供的总运能，其数学形式表示如下:

(3)运营水平(O)因素

反映货运系统运营水平较为典型的指标是服务水平(LOS)，运输系统的可靠性分析必须在某种服务水平前提下研究才有意义.考虑到货运系统中递送时间的重要性越来越突出，因此将平均行程时间作为服务水平的评价标准.也就是说第k类货物在OD点对w间的平均行程时间(x)应不大于其允许的最大时间，其数学形式表示如下:

式中，θk是与货种有关的参数，其取值范围从0～1，可根据实际调查数据预先确定是OD点对w间允许行程时间的上界，随不同的货类有不同的取值.

(4)环境影响因素

正如前文所提到的，环境因素对运输系统的影响越来越大，并且其涵盖的内容也相当广泛，为了便于分析，本文借鉴 Forkenbrock［8］(2001)提出的方法，对货运系统的外部环境因素进行定量化处理，如对环境污染、能源消耗等因素的考虑以货币化的外部成本形式出现，作为整个货运系统的约束条件之一，其数学形式可表示如下:

式中，φe是外部因素e∈E每吨公里的平均单位成本;E是外部影响因素的集合;da表示线段a的长度;则是单位时间内线段a上允许的最大外部成本.

(5)用户需求因素

货物的出行时间、运输方式、出行路径等选择将随着用户的不同而不同，并且随着不同区域的地理位置、人口构成、经济结构、社会发展水平等的不同，货运总需求也将发生相应的变化，但每个区域都有自身所能接受的最大需求量.为了便于分析，在此将额外的新需求与假定的固定需求相区分，并且假设新需求是一个变量，那么货种k在起点r的发生量和终点s的吸引量均应小于本区域所能容纳的上限，其数学形式表示如下:

因此，货物运输系统保留容量的求解，除了与式(5)～(8)下层网络平衡模型相联系外，还必须满足式(9)～(15)的约束条件.

3.3 货运系统可靠性分析模型

货物运输系统的容量可靠性可以理解为当相关变量发生变化时，整个货运系统的最大网络容量大于某一需求水平的概率，即所有线段或节点容量小于分配到的实际运量的概率.假设货运系统容量供给变动参数为β，则系统容量供给为:

式中，ci为系统容量的理想(最大)供给能力.如果以μ*代表需求水平，则容量可靠性满足μ*需求水平的计算公式如下:

很显然，当需求水平μ*为0时，货运系统100% 可靠，相反，如果需求水平μ*为无限大时，货运系统的可靠性为0%.保留容量概念的引入为计算和分析货运系统供给和需求变动时的系统可靠性问题提供了可能.

4 结论

货物单种运输方式的网络容量可靠性分析模型一般仅考虑该运输方式系统内的供给或需求变动对容量可靠性的影响，而综合货运网络可靠性模型除了考虑上述因素外，还要考虑用户出行方式选择、货运系统与外部环境之间的关系等问题.由于综合货运系统中各运输方式的外部成本不尽相同，在土地、能源、环境、资金等约束日益明显的今天，需要提出基于全成本理念的用户出行方式选择、路径选择的下层规划模型，从而推算整个系统的容量可靠性指标，以分析政府基础设施供给的经济性和结构合理性、需求管理措施的科学性和有效性等，避免供给过剩造成浪费或供给紧张影响经济社会的正常运行等问题的发生.本文只是在货运系统容量可靠性方面作了初步探索，今后还可以就相关参数的取值及确定方法、模拟方法的选择、模型的精简和优化等方面做进一步深入的研究和探讨.

［1］于世军.区域综合运输系统运输需求预测及评价指标体系研究［D］.南京:南京理工大学，2006.

［2］CHEN A，YANG H，LO H K，et al.A capacity related reliability for transportation networks［J］.Journal of Advanced Transportation，1999，33(2):183-200.

［3］CHENG L，LI Q，WANG J，et al.Urban street network capacity reliability［J］.Journal of Southeast University，2004，20(2):235-238.

［4］WEBSTER F V，COBBE B M.Traffic signal［R］.Road Research Technical，HMSO，London，1966:56.

［5］ALLSOP R E.Estimating the traffic capacity of a signalized road junction［J］.Transportation Research，1972(6):245-255.

［6］WONG S C，YANG H.Reserve capacity of a signal-controlled road network［J］.Transportation Research，1997，31B:397-402.

［7］CHEN A，TATINENI M，LEE D H，et al.Effect of Route Choice Models on Estimating Network Capacity Reliability［J］.Transportation Research Record，2000，1733:63-70.

［8］FORKENBROCK D J.Comparison of External Costs of Rail and Truck Freight Transportation［J］.Transportation Research，2001，35A:321-337.