土方调配和运输问题的两种实现方法
张现乐,王月明,欧阳靖雯
(西南科技大学土木工程与建筑学院,四川绵阳 621010)
土方工程中,通过土方调配计算确定施工区域填挖方区土方的调配方向和数量,以达到缩短工期和降低成本的目的。本文主要介绍了表上作业法进行土方调配的缺点和不足,以及常用软件Excel 的“规划求解”功能和LINGO 求解功能在土方调配计算中的应用。这两种方法避免了繁琐的求解过程,保证了求解的准确性和可靠性,为工程技术人员提供了简便的土方调配计算的方法。
1 问题描述及其数学模型
土方调配问题是指从不同的挖方区向不同的填方区运送土方,每个填方区需要特定数量的土方。问题是如何分配每个挖方区的土方供给,以便在满足每个填方区需求的条件下,优化某个目标,如最小全部费用或最小总运输量。设有m个挖方区Wi(i=1,2,…,m),设计的待挖土方量分别为si(i=1,2,…,m);有n个填方区Tj(j=1,2,…,n),设计需要填方量分别为dj(j=1,2,…,n);从i 到j 平均运输距离为cij。若用Xij表示从挖方区i 运往填方区j 的土方量,则在挖填平衡的条件下,土方的总运输量最小(若cij为从i 到j 运输单位土方的单价,则为总运费最小)的调运方案的数学模型为:
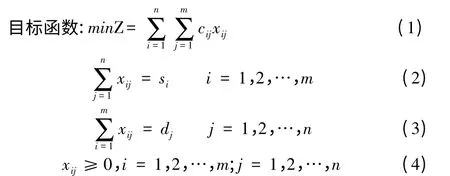
其中,式(1)为目标函数,即使土方总运输量最小;式(2)为挖方区的供给约束;式(3)为填方区的需求约束;式(4)为变量非负约束。
上述表达式为挖填平衡时的数学模型。当挖填不平衡时,依据挖、填方量的大小关系,土方调配问题的线性规划模型可分别表示如下[1]。
1.1 挖方量大于填方量
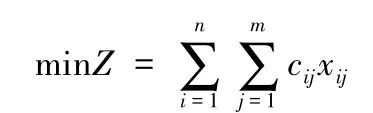
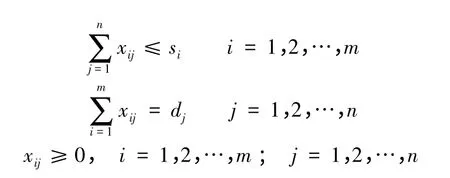
1.2 挖方量小于填方量
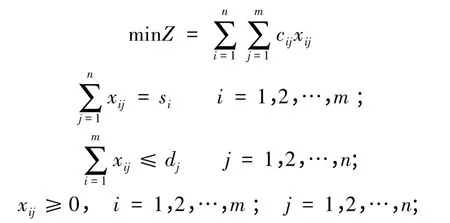
2 土方调配和运输问题的传统方法及其缺陷
2.1 传统方法的步骤
土方调配问题从实质上讲属于运筹学中的运输问题,它又分为平衡和不平衡两类。运输问题(TP)最早由Hieheoek和Kantorovic 两位学者提出,我国科学家王元、越民义等人率先开展研究,并于1959年前后获得了表上作业法等重要成果。表上作业法是当前我国解决土方调配问题通用的传统方法,其基本计算过程为:(1)通过西北角法、最小元素法、元素差额法(Vogel 法)中的一种方法找出初始基可行解。(2)运用闭回路法或位势法判别基可行解是否最优,当全部检验数非负时,取得最优解。(3)在表上用闭回路调整法进行调整,确定换入变量和换出变量,重复以上步骤直至找出新的基,获得最优方案[2]。
2.2 传统方法的缺陷
表上作业法在土方调配应用上的缺陷是由表上作业法作业过程和土方工程中土方调配的特点产生的,其缺陷主要表现在以下4个方面:
(1)计算过程比较复杂。表上作业法不仅要找出初始基可行解,还要反复计算检验数,检核正负值,判断是否最优和进行闭回路调优,整个过程比较繁杂。
(2)计算量大,数据处理任务艰巨。假定有m个挖方区、n个填方区,则求初始基可行解一般需要m+n-1 次加减运算;用位势法判优,需要经过解m+n-1 次一元一次方程计算位势和计算(m×n)-(m+n-1)个检验数,总计需要计算m×n 次;用闭回路法进行调整,若需要调整k 次,则中间环节共需要计算k×(m×n)次得最优解时,最优解方案的安排需要经过m+n-1 次加减运算得出。故全部过程一共需要经过2×(m+n-1)+k×(m×n)次运算[3]。由于土方工程中挖填区通常较多,即m 和n 值较大,从而导致表上作业法的计算量巨大,加之表上作业法多采用手工计算,因此实现起来比较困难。
(3)计算容易出错,进行正确性检核比较困难。由于表上作业法进行土方调配计算步骤特别多,加之人工计算,很容易出错,并且难以发现,逆序检核、纠错相当困难。
(4)工作效率低下。表上作业法步骤多、计算量大,并难以采用电子计算机快速解算,因而要完成大型土方调配方案的确定,通常耗时较长;同时,表上作业法针对性强,自动化和适应性较差,每遇到一个土方工程都要进行一轮计算,效率低下。
综上所述,表上作业法对土方调配区域较多的工程并非是一种十分有效的方法。实际上,表上作业法的理论基础是线性代数中的单纯形法,因而可以把土方调配这类运输问题作为线性规划问题来解决。线性规划是运筹学的一个重要分支,在数学上用以确定多变量线性函数在变量满足线性约束条件下的最优解,已经成为求解各种优化问题的主要方法。线性规划不仅理论成熟,而且可以通过计算机来实现。借助线性规划模型和Excel 软件“规划求解”功能或运用运筹学中LINGO 求解功能进行土方调配具有操作简便、计算快速准确的优点。
3 线性规划模型和Microsoft Excel 在土方调配和运输问题中的应用
3.1 依据土方工程的设计绘制填挖方平衡及运距表
在土方工程中,可以通过方格网法、横断面法和散点法等计算出各挖填区土方量和之间的平均运输距离,并绘制各调配区土方量和平均运距图。
例:某项目已知各土方调配区的土方量和相互之间的平均运距(图1),求最优方案。
为了求解方便,需要在Excel 中建一个填挖方土方量-运距表(见图2),将各调配区土方量和平均运距图中的数值填入其中,作为土方调配的依据。
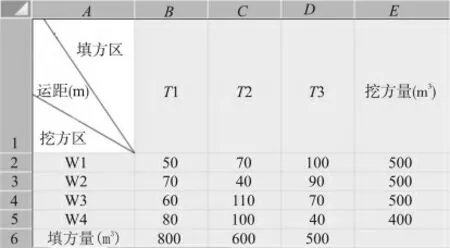
图2 填挖土方量-运距表
3.2 线性规划模型表达
在绘制出挖填土方量—运距表后,需要选择合适的线性规划模型,对土方调配问题进行具体数学表达,为利用Microsoft Excel 进行计算提供依据。本文以挖填平衡问题为例,挖填不平衡时土方调配方法与此类似。依据图2,则所举案例的线性规划数学模型应为:
目标函数:min Z=50×X11+70×X12+100×X13+…+80×X41+100×X42+40×X43
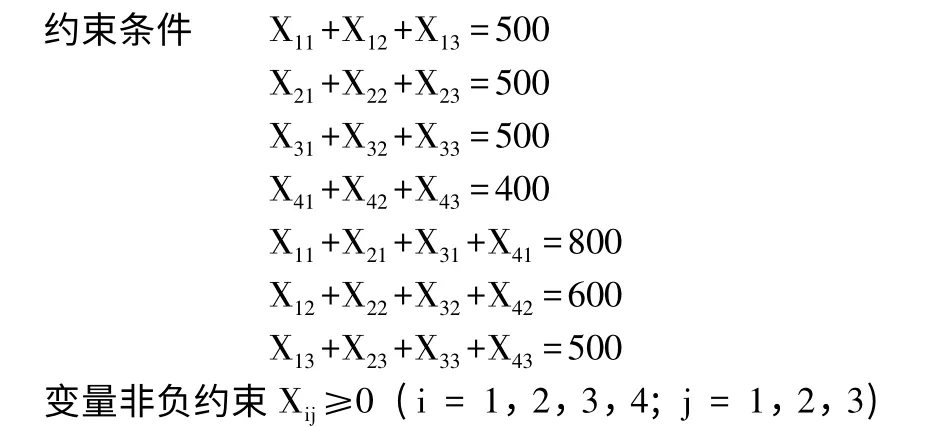
根据约束条件和上述计算式,可以得出未知量有4×3个,独立方程有4+3-1个,该方程有无穷多组解[4]。而通过Excel 的“规划求解”功能可以快速地求出一组最优解,使目标函数值为最小。
3.3 借助Excel 快速实现规划求解和土方调配
土方调配可以用“单纯形法”或“表上作业法”求解。但用“表上作业法”求解土方调配最优方案须轮流计算,计算量很大;用“单纯型法”则更繁琐。同时,无论是图解法还是用单纯形法,通常采用手工算法,计算起来比较繁琐,也很容易出错。
Excel 表具有强大的规划求解功能,具体操作步骤如下。
(1)在上述已建好的填挖方平衡及运距Excel 表中,接着建立如图3 所示单元格。
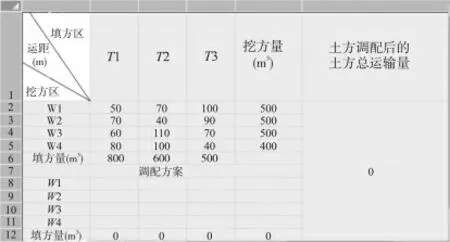
图3 目标单元格和可变单元格
其中,单元格B8:D11 与线性规划模型中变量Xij相对应,为可变单元格,保持原始值0 空置不填;单元格B12:D12和E8:E11为约束条件的部分表达式,在E8 单元格中输入公式“= SUM (B8:D8)”(即X11+X12+X13),在E9 单元格中输入公式“= SUM (B9:D9)”,在E10 单元格中输入公式“=SUM (B10:D10)”,在E11 单元格中输入公式“= SUM(B11:D11)”,在B12 单元格中输入公式“= SUM (B8:B11)”,在C12 单元格中输入公式“=SUM (C8:C11)”,在D12 单元格中输入公式“=SUM (D8:D11)”;单元格F2 与线性规划模型中目标函数的表达式相对应,是目标单元格,输入公式“=SUMPRODUCT (B2:D5,$B$8:$D $11)”,数学含义为“50×X11+70×X12+100×X13+…+80×X41+100×X42+40×X43”,实际含义为“土方总运输量”。计算式中$ B $8:$D $11为绝对地址,这样做是为了方便计算式的复制。按上述输入后,单元格B12:D12、E8:E11 和F2 的值暂时变为0,见图3。
(2)加载“规划求解”程序。一般情况下,Microsoft Excel软件中规划求解的功能都尚未安装,需要加载。单击“工具”菜单,然后点击“加载宏”,然后在弹出菜单中选中“规划求解”项,最后单击“确定”即可。
(3)设置“规划求解参数”。点击“工具”中的“规划求解”选项打开规划求解参数设置页面。在“设置目标单元格中”填入“$F$2”,在“等于”选项中选择“最小值”,在“可变单元格”选项中填入“$B$8:$D$11”。在“约束”选项中点击“添加”按纽,添加约束条件“$ B $12:$ D $12=$B$6:$D$6、$ E $8:$ E $11=$ E $2:$ E$5 和$B$8:$D$11 ≥0”。点击“选项”按钮出现“规划求解选项”对话框,选定“采用线性模型”和“假定非负”复选项,其中的“迭代次数”选项参数可以随着精度的要求决定。
(4)求解。规划求解参数全部设置好之后,即可点击“求解”按钮进行计算,弹出“规划求解结果”对话框后,点击“确定”后便得到求解结果(见图4 所示)。
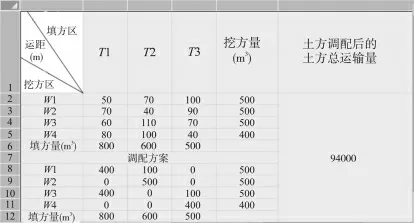
图4 土方调配方案
从图4 中可以看出土方的调配方案为:挖方区W1 分别运往填方区T1、T2 土方400 m3和100 m3,挖方区W2 需要运往填方区T2 土方500 m3,挖方区W3 需要分别运往填方区T1、T3 土方400 m3和100 m3,挖方区W4 需要运往填方区T3土方400 m3,土方调配后土方总运输量为94000 m3。
(5)检验结果。为了防止计算出错,可以通过单元格B12:D12 与B6:D6 以及E8:E11 与E2:E5 对比分析检验输入是否出错。如果两者一致说明正确无误,如果不一致则说明单元格数据输入或规划参数设置出错,需要检查纠正。经检验,本次计算正确无误。
(6)绘制土方调配图。为了方便工程施工需要将得出来的调配方案绘制成土方调配图,见图5。

图5 土方调配图
4 采用运筹学中LINGO 程序求解
当在Windows 下开始运行LINGO 系统时,会得到类似图6 的一个窗口。
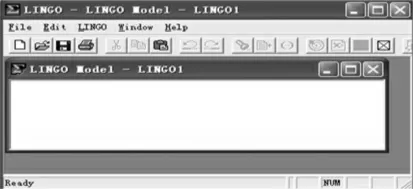
图6 Windows 开始运行LINGO 系统时的窗口
其中外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。在主窗口内的标题为LINGO Model-LINGO1 的窗口是LINGO 的默认模型窗口,建立的模型都要在该窗口内编码实现。
而采用LINGO 求解上面的例题,需要输入程序:


然后点击工具条上的求解按钮即可求得结果。经检验,所求得结果与用Excel 求解得到的结果一样。而运用LINGO的程序求解更方便,它可以用于一切的土方调配和运输问题。如果是小型土方平整,也可以不输入程序,直接输入前面提到的线性规划数学模型,即可求得结果。经过笔者检验,完全可以实现。
5 Microsoft Excel 规划求解功能和LINGO 求解功能的
利用Excel 规划求解功能和LINGO 求解功能求解土方调配问题的方法适用范围较广,它们不仅适用于挖填平衡条件下的土方调配,而且也适用于挖填不平衡的情况,即可以应用于所有线性运输问题(LTP)。挖填不平衡时,只需采用相应的线性规划模型并改变Excel“规划求解参数设置”约束条件即可,而LINGO 只需在模型窗口中改变约束条件即可。Excel 计算表在土方调配中可以重复使用,效率较高。当土地平整工程和土方调配任务发生变化时,只需根据挖填区个数在图4 中删除或插入相应的单元格即可,而Excel 计算表的公式和规划求解参数通常无需修改。此外,如果需要经常性进行土方调配工作,还可设置“清空数据”和“土方调配”等命令按纽以及快捷菜单,方便清除数据,达到优化用户操作界面的目的。而利用LINGO 程序求解则无需这样。
需要注意的是,运用Excel 规划求解功能求解计算出来的结果一定最优,但可能并非惟一,所得方案只是最优方案中的一种,是否存在惟一解,需通过位势法求来检验。若非基变量的检验数全部大于0,则所求解为惟一最优解;若存在非基变量的检验数等于0,则说明存在非惟一最优解。此时,只要把检验数为0 的非基变量作为入基变量,调整运输方案,即可得到另一个最优方案。而LINGO 求解计算出来的结果一定最优,且可以得到所有的最优方案。
8 结束论
本文介绍了借助线性规划模型和Microsoft Excel“规划求解功能”求解以及LINGO 求解土方工程中土方调配问题的方法,与传统的表上作业法相比,这两种方法具有方便、快捷、准确的优点,尤其在挖、填区较多情况下,这样的优势将更加明显。同时,这两种方法也可推广应用于所有线性运输问题(LTP )和最短路径问题的求解。
[1]刘立群.土方调配优化中运筹方法的改进[J].工业技术经济,2001(4):61-63
[2]李时椿.运输问题表上作业法的改进研究[J].南京航空航天大学学报,2000,32 (3):324-329
[3]贾春玉.运输问题新解法的探讨[J].系统工程学报,2005,19(2):208-217
[4]郑文魁,徐胜春.“规划求解”在土方调配计算中的应用[J].水利科技与经济,2006,12 (10):678-686

