大跨劲性骨架拱桥外包混凝土浇注方案
张富贵,张永水,董 义,吴世曾
(重庆交通大学土木建筑学院,重庆400074)
近几年来,钢管混凝土拱桥建设技术得到了迅速发展,成为我国近年来桥梁建筑发展的新技术。它是利用型钢、钢管作劲性骨架,然后在其基础上搭模板分段分层浇筑混凝土,最后形成劲性骨架钢筋混凝土拱桥。这种桥型充分发挥了各自材料的特长,克服了大跨拱桥的施工困难,跨越能力很大[1-2]。
1 工程概况
昭化嘉陵江大桥为上承式劲性骨架施工的钢筋混凝土箱形拱桥,主桥长364 m。主拱采用等截面悬链线无铰拱。钢管外包C55混凝土,拱圈采用两拱肋,两肋间以横联连接,每拱肋为单箱双室截面,横向采用等宽8 m,纵向采用外形等高5.8 m,标准段顶、底板厚0.4 m,腹板厚0.3 m。拱圈拱脚至第2根拱上立柱间为渐变段,顶、底板混凝土厚度由0.8 m线性变化至 0.4 m,边腹板厚度由 0.55 m 线性变化至0.3 m,中腹板厚度保持不变。
劲性骨架为型钢与钢管混凝土组成的桁架结构,每肋上、下各3根φ457×14 mm、内灌注C80混凝土的钢管混凝土弦杆。弦杆通过横联角钢和竖向角钢连接而构成型钢-钢管混凝土桁架,在拱肋横联对应位置设交叉撑,加强横向连接。腹杆及平联与弦杆均采用焊接连接。
拱圈浇注:待劲性骨架弦管内混凝土全部达到设计强度后,方可浇注拱圈混凝土。拱圈混凝土的浇注采用“先底板,再腹板,最后顶板”的浇注方式,即先按上、下游对称且两岸对称方式分多工作面浇注底板直至合龙,然后再按照同样的方式浇注腹板、顶板。主桥桥型布置如图1。
2 外包混凝土浇注方案
浇注方案考虑竖向分3环,纵向分不同的段,按照不同的工作面和工作段进行比较。方案1纵向分8段,底板、腹板分8个工作面10个工作段两拱肋对称浇注,顶板分4个工作面10个工作段两拱肋对称浇注;方案2纵向分16段,底板、腹板分16个工作面5个工作段两拱肋对称浇注,顶板分8个工作面5个工作段两拱肋对称浇注。主拱圈外包混凝土浇注示意如图2,外包混凝土浇注方案见表1。图2中钢管编号依次为下弦管1#(中)、3#(内)、4#(外),上弦管2#(中)、5#(内)、6#(外)。
3 模型建立
根据钢管混凝土拱肋的材料特性并结合本桥的实际情况,不考虑钢管与管内混凝土的联合作用,按照双单元法来计算[3]。
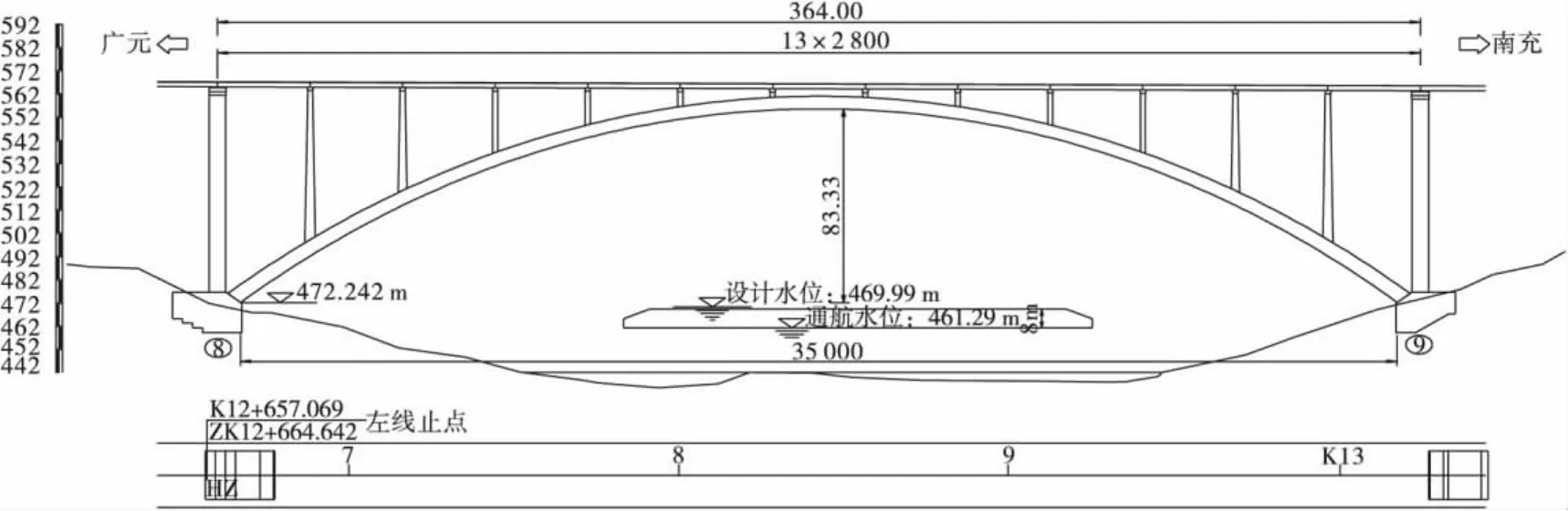
图1 主桥立面(单位:m)Fig.1 Main bridge elevation

图2 主拱圈外包混凝土浇注示意Fig.2 Schematic diagram of the main cast concrete arch outsourcing

表1 外包混凝土浇注方案Table 1 Outsourcing concrete pouring scheme
本桥拱肋外包混凝土施工计算采用Midas Civil 2010建立拱箱的梁-板组合有限元模型,主拱圈按实际构造离散为1 209个结点、7 796个单元,其中钢管混凝土劲性骨架为4 974个梁单元、拱箱混凝土为2 802个板单元。钢骨架各杆件之间采用刚结点连接,骨架和板单元之间采用虚拟刚性梁的刚臂方式处理,对拱脚结点采用固结约束,如图3。

图3 主拱圈Midas Civil模型Fig.3 Midas Civil model of main arch
4 不同浇注方案的受力状态分析
考虑到劲性骨架在外包施工过程中,外包混凝土后的钢管混凝土受其周围混凝土的约束力而共同受力,会发生应力重分布,认为钢管混凝土的最不利状态发生在其未外包混凝土时[4]。因此钢管混凝土劲性骨架下弦杆最不利状态发生在浇注底板混凝土时,上弦杆最不利状态发生在浇注顶板混凝土时。
4.1 最不利状态下劲性骨架受力状态分析
4.1.1 方案 1
下弦杆最不利状态发生在底板 B、C、D段中B10、C10、D10节段混凝土的浇注施工时,上弦杆最不利状态发生在顶板B、D段中B9、B10、D9、D10节段混凝土的浇注施工时。
4.1.2 方案 2
下弦杆最不利状态发生在底板 B'、C'、D'、E'、F'、G'、H'段中 B5'、C5'、D5'、E5'、F5'、G5'、H5'节段混凝土的浇注施工时,上弦杆最不利状态发生在顶板 B'、D'、F'、H'段中 B5'、D5'、F5'、H5'节段混凝土的浇注施工时。
图4为底板合龙时,上、下弦杆钢管应力图。

图4 底板合龙钢管应力Fig.4 Diagram stress of steel of base plate closure
底板合龙时,下弦钢管应力方案1与方案2相比最大值相差不大,但是方案2的钢管应力曲线的波动性变化比较大;上弦钢管应力最大值方案2比方案1大17 MPa,而且方案2的钢管应力整体比方案1大,这是因为方案2分段浇筑的混凝土数量比方案1大。
图5为腹板合龙时,上、下弦杆钢管应力图。

图5 腹板合龙钢管应力Fig.5 Diagram stress of steel of webs closure
腹板合龙时,下弦钢管应力方案1与方案2相比最大值仍相差不大,方案2的钢管应力曲线的波动性没有明显变化,这是由于分段数量的不同造成的;上弦钢管应力方案2比方案1略大,但只是在拱脚区域有所差别,其他区域差别不大。
图6为顶板合龙时,上、下弦杆钢管应力图。

图6 顶板合龙钢管应力Fig.6 Diagram stress of steel of roof closure
顶板合龙时,下弦钢管应力方案1与方案2相比最大值仍相差不大;方案1与方案2相比上弦钢管应力有了明显变化,方案1钢管应力比方案2要小一些,特别是在拱脚处要小许多,方案1管内混凝土应力曲线更平滑些,数值波动不大,这是由于顶板板混凝土参与受力对上弦杆应力产生了重新分配。
顶板合龙时,管内C80混凝土的应力达到最大值,方案1上弦杆内混凝土压应力最大值为25.2 MPa,方案2为26.1 MPa,两者相差不大;方案1下弦杆内混凝土压应力最大值为27.5 MPa,方案2为29.2 MPa,比方案 1 的要大 1.7 MPa。管内混凝土应力满足结构的受力要求[5]。
成拱后,从拱脚到3/8截面处,方案1和方案2挠度变化基本一致,但是从3/8截面到拱顶截面处方案2下挠值比方案1要大,在拱顶处两者相差约5 cm(图7)。

图7 成拱后拱圈下挠Fig.7 Deflection diagram of the arch ring after arched
4.2 不同浇注方案对劲性骨架稳定的影响
劲性骨架拱桥施工成败的关键是施工过程中的稳定性问题,因此还必须对其进行稳定性计算[6-8]。表2列举出了拱圈外包浇注每一段时结构的稳定系数,以反映整个拱圈外包浇注过程结构的稳定性。

表2 外包浇注各施工阶段线弹性稳定性Table 2 Outsourcing pouring elastic stability of the construction phase
从表2中可以看出,方案1在底板的浇注过程中结构处于最不利稳定状态,稳定系数较小,但在合龙时达到较大1值。但方案2在底板、腹板的浇注过程中结构始终处于最不利稳定状态,稳定系数都比较小,合龙时达到较大值。这是由于方案2浇注的混凝土数量要大许多;腹板、顶板浇注施工过程中结构的稳定系数表现为先逐步增大、再减小、最后在逐步增大的变化趋势,且都在合龙时达到阶段最大值。底板、腹板和顶板合龙后方案1与方案2的稳定系数相差不大。因此从稳定性的角度来说方案1要比方案2要好,更利于施工时结构的稳定。
5 结语
通过对劲性骨架拱桥拱圈外包混凝土的不同浇注方案进行比较分析,还从稳定方面对外包浇注过程中结构的安全性给出评价,得出如下结论:
1)拱圈外包混凝土浇注中方案1与方案2相比,受力方面两者对骨架的应力水平有影响,方案1的应力曲线比方案2相对平滑些,在底板合龙时方案1的上弦杆压应力最大值明显比方案2要小,而且采取方案1可以明显降低成拱后拱圈的下挠值。
2)稳定性方面:无论是采用方案1和方案2,拱圈外包浇注的过程中,结构的稳定系数均大于4,采取方案1的浇注方式,仅在浇注底板的过程中结构的稳定性较低,而采取方案2,不仅是在浇注底板的过程中结构的稳定性较低,而且在浇注腹板的过程中结构稳定性仍然较低。
[1]邱麟,孙吉飚.钢管混凝土劲性骨架拱桥施工阶段稳定性分析[J].重庆交通大学学报:自然科学版,2008,27(3):366 -369.Qiu Lin,Sun Jibiao.Analysis on stability of concrete filled steel tube arch bridge in construction[J].Journal of Chongqing Jiaotong University:Natural Science,2008,27(3):366-369.
[2]周水兴,顾安邦.大跨径劲性骨架钢筋混凝土拱桥徐变收缩时效分析[J].重庆交通学院学报,1996,15(1):1 -10.Zhou Shuixing,Gu Anbang.Creep-shrinkage time-dependent analysis of large span reinforced concrete arches of stiffen framework[J].Journal of Chongqing Jiaotong Institute,1996,15(1):1 -10.
[3]张犇.大跨劲性骨架混凝土箱拱桥施工优化设计[D].重庆:重庆交通大学,2011.
[4]刘剑.大跨径钢管混凝土劲性骨架拱桥主拱圈施工方案研究[D].西安:长安大学,2007.
[5]JTG D 6—2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004.
[6]陈宝春.钢管混凝土拱桥设计与施工[M].北京:人民交通出版社,1999.
[7]谢尚英,钱冬生.劲性骨架施工阶段非线性稳定分析[J].土木工程学报,2000,33(1):23 -26.Xie Shangying,Qian Dongsheng.Non-linear stability analysis of concrete arch bridge with stiff skeleton of concrete filled steel tubes during construction [J].China Civil Engineering Journal,2000,33(1):23- 26.
[8]李国豪.桥梁结构稳定与振动[M].修订版.北京:中国铁道出版社,2003.

