中国制造业空间集聚对全要素生产率的影响机理研究——基于双门限回归模型的实证分析

王 燕，徐 妍

（1.南开大学 经济与社会发展研究院，天津300071；2.南开大学 城市与区域经济研究所，天津300071）

一、引 言

产业空间集聚问题的研究始于Marshall（1890），其产业区理论从外部经济的角度指出特定产业部门在特定地区集聚有利于提高生产效率。随后，国外学者对这一问题进行了多方面的研究。从成本最小化的角度，Weber（1909）在工业区位论中指出，只有当集聚所增加的运费小于或等于其所节约的生产成本时，企业才会选择在某一地点集聚；从规模经济的角度，Hoover（1936）的产业集聚最佳规模论指出，产业空间集聚存在一个适度的规模，集聚企业太少达不到规模经济的效果，集聚企业太多则可能由于某些原因而导致规模不经济并使集聚整体效应下降；从创新的角度，Porter（1990）、Saxenian（1994）等人先后强调，集群内部的企业与供应商、竞争对手乃至政府和协会等机构之间的互动合作有利于技术创新和扩散，这种集群式创新在市场需求快速变化的今天是获取产业持久竞争力的重要源泉；从规模报酬递增的角度，Krugman（1991）认为，市场规模效应、稠密的劳动力市场以及外部经济是促使产业空间集聚的主要力量，由历史和偶然的因素所决定的区域初始优势还会使产业空间集聚进入“自我锁定”的累积循环路径。

关于产业空间集聚对全要素生产率的影响机理问题，国内已有一些学者进行了实证研究，主要是通过测算近年来中国部分制造行业的TFPMalmquist指数和空间基尼系数，并利用固定效应模型或门限回归模型展开分析，所得结论不完全相同。有的认为产业空间集聚主要通过推动技术进步来提高全要素生产率（赵伟、张萃，2008），有的则认为产业空间集聚主要通过提高技术效率来提高全要素生产率（王丽丽、范爱军，2009），还有的将空间基尼系数与出口密集度的乘积项纳入分析模型，认为尽管产业空间集聚与出口都有利于提高全要素生产率，但两者的交互影响却会削弱它们各自对全要素生产率的促进作用（张公嵬、梁琦，2010）。

在现有研究的基础上，本文试图做如下改进：一是用EG指数替代空间基尼系数。EG指数的构造以赫芬达尔指数和空间基尼系数为基础，充分考虑了区域规模和企业规模对产业空间集聚程度的影响；空间基尼系数则不能有效识别产业空间集聚是源于“少数规模庞大的企业在同一区域的市场集中”，还是源于“许多家中小企业在同一区域的地理集中”。二是用双门限回归模型替代传统的个体固定效应模型，门限回归模型不仅在一定程度上克服了个体固定效应模型不变系数所造成的估计误差，而且双门限的设定能够更有效地反映产业空间集聚影响全要素生产率的内在规律。

鉴于此，本文根据中国2000－2008年20个制造行业的面板数据，利用数据包络分析法测算了分行业的TFP－Malmquist指数及其分解，并采用EG指数衡量分行业的空间集聚水平，在引入其他控制变量的基础上建立了以产业空间集聚水平为门限变量的双门限回归模型，以期望回答三个问题：第一，产业空间集聚与全要素生产率是否相关？第二，产业空间集聚通过何种途径对全要素生产率产生影响？第三，产业空间集聚对全要素生产率的影响是否存在门限效应？

二、模型与数据处理

（一）门限回归方法

考虑到产业空间集聚对全要素生产率的影响大小可能会随集聚水平的变化而有所不同，需要依据一定的门限值对样本行业及其空间集聚水平进行区间划分。传统回归方法所用到的门限值往往由研究者根据个人经验确定，其主观随意性较强。因此，本文采用Hansen（1999）提出的门限回归方法，该方法以“残差平方和最小化”为原则来确定门限值，同时对门限效应的显著性进行了检验，从而使门限值的科学性和可靠性得到保证。

其中，yit为被解释变量，qit为门限变量，η为门限值为解释变量向量和为系数向量，εit为服从独立同分布的随机扰动项，μi为个体截距项。此外，为外生变量，与εit不相关；qit可作为解释变量，也可仅作为门限变量而非解释变量；I｛·｝为示性函数，若括号中的表达式为真，其取值为1，反之，其取值为0。通过定义与，单门限回归模型可转化为参数（β1，β2）的线性函数：

利用转化后的模型对η进行估计，具体步骤为：首先，将qit的n个观测值逐一作为门限值进行OLS估计，得到n组估计量（（η）（η））及残差平方和SSR（η）；其次，选取使SSR（）为最小残差平方和，由此得到合意的参数估计值（）（），）；最后，对门限效应进行显著性检验。原假设H0—，备择假设H1≠—，检验统计量。其中，SSR＊为原假设成立时的残差平方和）为εit的方差的一致估计量。显然，），故（）越大越倾向于拒绝原假设，即存在门限效应。类似地，双门限回归模型可表示为：

（二）制造业空间集聚的双门限回归模型

由于回归结果显示存在双门限值，本文将分析模型设定为：

其中，i表示行业，t表示年份。

被解释变量分别为全要素生产率累积指数、技术进步累积指数和技术效率累积指数，由各行业历年的TFP－Malmquist指数及其分解通过逐年累积相乘得到。之所以采取累积形式是考虑到TFP－Malmquist指数及其分解衡量的是以上一年为基期的相对效率，EG指数则衡量的是产业空间集聚的绝对水平，不能直接对两类指数进行回归。

门限变量为产业空间集聚水平，用各行业历年的EG指数表示。

由于影响全要素生产率的因素较多，不能只考虑空间集聚的单方面作用，故引入五个控制变量：（1）企业规模，若不考虑企业在组织管理、人员监督等方面的交易成本，企业规模的扩大有助于产生规模经济及边际收益递增，从而企业生产率得以提高，并带动行业全要素生产率增长；（2）研发活动，通常有助于技术进步，从而提高全要素生产率；（3）外商直接投资，通过技术溢出促进行业技术进步，从而提高全要素生产率；（4）贸易开放度，出口将通过“出口中学”和竞争效应对行业的生产技术和效率产生促进作用；（5）盈利能力，企业的盈利能力增强有利于引进专业型人才、先进技术设备等，从而提高企业的生产效率，促进行业全要素生产率增长。

表1 各变量的相关说明

（三）数据来源与处理

为保证统计口径的一致性，本文选取在新、旧国民经济行业分类体系（GB／T4754－2003和GB／T4754－1994）中未作改动的20个制造行业予以分析，区域划分指中国内地的30个省（区）、直辖市（不包括西藏），时间跨度为2000－2008年。所需数据来源于历年的《中国工业经济统计年鉴》、《中国固定资产投资统计年鉴》和《中国城市（镇）生活与价格年鉴》。

1.分行业的TFP－Malmquist指数及其分解

根据面向产出、规模报酬可变的DEA－Malmquist模型和处理后的产出、投入数据，本文使用DEAP2.1计算出分行业的TFP－Malmquist指数及其分解。其中，产出以工业总产值（亿元）表示，用工业品出厂价格指数将当年价产出平减为1999年不变价产出；劳动力投入以全部从业人员年平均人数（万人）表示；资本投入以年末固定资产净值（亿元）表示，用固定资产投资价格指数将当年价资本投入平减为1999年不变价资本投入。

2.分行业的EG指数

EG指数由Ellison和Glaeser（1997）依据镖靶模型（Dartboard）推导得出。在该模型中，企业追求利润最大化，其区位选择受到区域自然优势、产业技术溢出的影响，最终在特定区域内形成“群聚”现象。假设某一经济体被划分为m个区域，在这些区域内分布着行业i的n个企业，则行业i的EG指数（γi）的计算公式为：

其中，xj为区域j所有行业的总产值占全国所有行业总产值的比重，sij为行业i在区域j的总产值占该行业全国总产值的比重，zik为企业k的产值占行业i总产值的比重，Gi和Hi分别为行业i的空间基尼系数和赫芬达尔指数。γi∈［0，1］，γi越大，说明行业i的空间集聚程度越高。

由于缺乏单个企业的详细数据，本文假设行业i在区域j内分布的nij个企业具有相同的产值规模，则调整后的赫芬达尔指数的计算公式为：

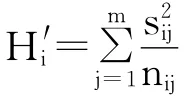
从推导过程看，企业相对规模的变化只会影响赫芬达尔指数的大小，而不会改变EG指数作为产业空间集聚程度的无偏估计量的统计特性。从实际情况看，中国制造业的市场集中度仍比较低，2003－2008年，30个2－SIC行业中有29个为原子型市场结构，只有烟草制品业为低集中寡占型市场（葛顺奇、李圆圆，2010）。这种高度分散化、竞争型的市场结构意味着无论在全国还是省级地区，产业内部的企业，特别是市场份额排名靠前的企业之间在产值规模上不会有过于显著的差异，从而使本文假设具有一定的合理性。因此，上述简化引起的估算偏差并不妨碍后续分析。

三、实证结果分析

本文利用STATA11.0得到不同被解释变量的双门限回归模型和个体固定效应模型的估计结果（见表2），通过对比两类模型中EG指数的回归系数可以进一步佐证门限效应的存在。此外，表3还给出不同被解释变量的门限估计值、样本区间划分以及20个制造行业在不同样本区间的分布情况。①

表2 双门限回归模型和个体固定效应模型的估计结果及对比

续表2 双门限回归模型和个体固定效应模型的估计结果及对比

表3 20个制造行业在不同样本区间内的分布情况

（一）产业空间集聚与全要素生产率的相关性

表2显示，在门限回归模型的三个区间中，TFP对EG的系数都为正且在1%或5%的水平上显著。这说明产业空间集聚对全要素生产率具有正向影响，全要素生产率将随产业空间集聚的加深而有所提高。在固定效应模型中，TFP对EG的系数也为正且在1%的水平上显著，再次印证了产业空间集聚会促进全要素生产率增长的观点。

（二）产业空间集聚对全要素生产率的影响途径

表2显示，在门限回归模型的三个区间中，TECH对EG的系数都为正且在1%的水平上显著，EFF对EG的系数在区间1和区间2中为正且通过了显著性检验，在区间3中为负且不显著。这说明产业空间集聚对技术进步和技术效率都具有正向影响，但对技术效率的影响只在有限的集聚水平范围内显著。

表3显示，TFP的η1与TECH的η1同为0.0330，故它们的区间1包含了相同的样本数据和行业；EFF的η2为0.0282且小于TFP和TECH的η1，故EFF的区间1和区间2中的样本数据和行业都包含在TFP和TECH的区间1中，EFF的区间3则包含了TFP和TECH的区间2和区间3中的全部样本数据和行业，也包含了TFP和TECH的区间1中的个别样本数据和行业。于是，EFF的区间1中的行业就满足“TECH对EG的系数（33.5612）＞TFP对EG的系数（21.7064）＞EFF对EG的系数（9.0905）”，区间2中的行业就满足“TECH对EG的系数（33.5612）＞TFP对EG的系数（21.7064）＞EFF对EG的系数（3.6150）”。对于区间3中的行业而言，情况比较复杂，如C40，其TECH对EG的系数对应为13.2090或6.8373，而TFP对EG的系数只对应为5.2647；又如C41，当其TECH对EG的系数对应为13.2090时，TFP对EG的系数对应为12.1406或5.2647，当其TECH对EG的系数对应为6.8373时，TFP对EG的系数只对应为5.2647。尽管如此，这些行业仍满足“TECH对EG的系数＞TFP对EG的系数＞0＞EFF对EG的系数（－0.2855）”。综上所述，产业空间集聚主要通过促进技术进步和提高技术效率两个途径对全要素生产率产生正向影响，并且在前一途径中对技术进步的影响相对较大。

（三）产业空间集聚影响全要素生产率的门限效应

表2显示，在TFP的门限回归模型中，F值在5%的水平上显著，从统计学意义上肯定了门限效应的存在；从区间1到区间3，TFP对EG的系数逐次递减，即门限效应表现为伴随产业空间集聚的加深，其对全要素生产率的影响将逐步减弱。对比发现，固定效应模型中TFP对EG的系数虽然与门限回归模型区间3中TFP对EG的系数接近，但仅为区间1和区间2中相应系数的25%和45%。这种差异说明，基于固定效应模型的实证分析可能会“掩盖”门限效应存在的事实，相比之下，双门限回归模型则能更准确、深入地揭示出产业空间集聚对全要素生产率的影响机理及其内在规律。以TECH和EFF为被解释变量的门限回归模型的估计结果显示，产业空间集聚对技术进步和技术效率的影响也都存在门限效应，其影响大小与集聚水平呈反方向变化。

我们进一步考察能否结合行业的技术特性来理解门限效应。表3显示，就TFP而言，C14、C15、C22、C25、C26、C27、C31、C33、C34、C35、C36、C37和C39稳定分布于区间1，②C13、C17和C32稳定分布于区间2，C16、C28、C40和C41稳定分布于区间3。就TECH而言，其区间3要求“γi≥0.0641”，故导致稳定分布于其中的行业减少为C16、C28和C40，但行业分布的总体情况与TFP基本一致。就EFF而言，C22、C26、C27、C31、C34和C36稳定分布于区间1，C15、C33、C35、C37和C39稳定分布于区间2，C13、C16、C17、C25、C28、C32、C40和C41稳定分布于区间3。根据经合组织（OECD）对制造业技术层级的划分标准，无论是TFP还是TECH，区间1和区间2中的稳定行业都主要为中低技术行业和大部分资源性行业，区间3中的稳定行业则为高技术行业（C40和C41）、中技术行业（C28）和资源性行业（C16）；相反，EFF所对应的行业分布情况却没有表现出明显的技术梯度特点，处于不同技术层级的行业在EFF的三个区间中都有分布。综上所述，若不考虑个别情况，行业的技术特性与门限效应之间就存在某种关联——伴随行业技术层级的提升，其空间集聚对全要素生产率和技术进步的促进作用逐渐减弱。

（四）控制变量对全要素生产率的影响

从表2可以看出：其一，FDI、TRADE和EP都是影响技术进步和全要素生产率的积极因素，但对提高技术效率却相对乏力；其二，TFP和TECH对SCALE的系数均为负，与表1中的预期不同，这可能是因为本文以平均从业人员数来衡量企业规模，而劳动力规模的不断增加容易引发人员组织庞杂、管理效率低下等问题，对企业的技术效率会造成一定的负面影响；其三，R＆D有助于提高全要素生产率和技术效率，但对技术进步的促进作用尚未充分显现，这可能源于国内专业型研发人员比较匮乏，企业仍主要依赖于“引进、消化、吸收、创新”和“集成创新”等基础创新模式而“原始创新”不足，加之研发活动风险高、见效慢，这些因素都不同程度地造成研发活动对技术进步的促进作用相对“疲软”。

四、结论与启示

通过实证研究，本文在引言中所提及的三个问题已得到初步解答，主要结论及其启示可归纳为以下几个方面：

第一，产业空间集聚可通过促进技术进步和提高技术效率两个途径来提高全要素生产率，并且空间集聚对技术进步的作用远大于对技术效率的作用。由于我国制造业空间集聚往往附着大量的资本投入，主要表现为资本品在质量上的提高或改进，包括新资本品的发明和引进，因而更多地促进了体现型技术进步（Embodied Technical Change，ETC），而对与资源优化配置、效率改进等相关的非体现型技术进步却作用有限。

第二，产业空间集聚对全要素生产率、技术进步和技术效率的影响都存在门限效应，其影响将伴随集聚水平的提高而逐步弱化。这一结论表明产业空间集聚对全要素生产率的影响遵循了边际效应递减规律，过度集聚会产生污染集中、地价上涨、恶性竞争等生产要素拥挤效应。这些集聚成本的积累会在一定程度上削弱企业在技术创新、效率改进等方面的潜能，使产业空间集聚对全要素生产率、技术进步和技术效率的作用强度有所减弱，从而用中国制造业的发展实践验证了Hoover（1936）关于产业空间集聚存在一个最佳规模的论断。

第三，多数资源性行业和中低技术行业的EG指数长期低于0.0459，EG指数每增大0.01，全要素生产率累积指数和技术进步累积指数将分别增加0.1692和0.2339。而通信设备、计算机及其他电子设备制造业、仪器仪表及文化、办公用机械制造业、烟草制品业和化学纤维制造业等行业，虽然EG指数处于0.0563－0.1617的高位，但EG指数每增大0.01，以上两个指数仅分别增加0.0527和0.0684。这一结论表明，对于全要素生产率和技术进步而言，产业空间集聚的边际效应递减规律在行业技术特性上也有所体现：技术层级较高的行业，其集聚水平也较高但集聚效应较低；技术层级较低的行业，其集聚水平也较低但集聚效应较高。然而，技术效率未表现出类似的行业技术梯度特征。

注释：

①C13——农副食品加工业，C14——食品制造业，C15——饮料制造业，C16——烟草制品业，C17——纺织业，C22——造纸及纸制品业，C25——石油加工、炼焦及核燃料加工业，C26——化学原料及化学制品制造业，C27——医药制造业，C28——化学纤维制造业，C31——非金属矿物制造业，C32——黑色金属冶炼及压延加工业，C33——有色金属冶炼及压延加工业，C34——金属制品业，C35——通用设备制造业，C36——专用设备制造业，C37——交通运输设备制造业，C39——电气机械及器材制造业，C40——通信设备、计算机及其他电子设备制造业，C41——仪器仪表及文化、办公用机械制造业。

②“某一行业稳定分布于某一区间”是指，该行业在2000－2008年至少有5年的EG指数包含在该区间中。

［1］赵伟，张萃.中国制造业区域集聚与全要素生产率增长［J］.上海交通大学学报（哲学社会科学版），2008，（5）：52－56.

［2］王丽丽，范爱军.空间集聚与全要素生产率增长——基于门限模型的非线性关联研究［J］.财贸经济，2009，（12）：105－110.

［3］张公嵬，梁琦.出口、集聚与全要素生产率增长——基于制造业行业面板数据的实证研究［J］.国际贸易问题，2010，（12）：12－19.

［4］葛顺奇，李圆圆.外商直接投资对我国制造业市场集中度的影响［J］.国际经济合作，2010，（9）：24－31.

［5］〔英〕马歇尔.经济学原理［M］.北京：商务印书馆，1964.

［6］〔德〕阿尔弗雷德·韦伯.工业区位论［M］.北京：商务印书馆，1997.

［7］〔美〕埃德加·M.胡佛.区域经济学导论［M］.北京：商务印书馆，1990.

［8］〔美〕迈克尔·E.波特.国家竞争优势［M］.北京：华夏出版社，2002.

［9］Saxenian A.Regional advantage：Culture and competition in silicon valley and route 128［M］.Cambridge MA：Harvard University Press，1994.

［10］Hansen B E.Threshold effects in non－dynamic panels：Estimation，testing and inference［J］.Journal of Econometrics，1999，93（2）：345－368.

［11］Ellison G，Glaeser E L.Geographic concentration in U.S.manufacturing industries：A dartboard approach［J］.Journal of Political Economy，1997，105（5）：889－927.