一种改进的多叶准直器射野分割算法

张鹏程 朱 健，2 李元金，3 舒华忠

(1东南大学影像科学与技术实验室，南京210096)

(2山东省肿瘤医院，济南250117)

(3滁州学院计算机科学与技术系，滁州239000)

在调强放疗(intensity-modulated radiotherapy，IMRT)计划的实施过程中，可以采用多叶光栅静态调强和多叶光栅动态调强2种模式.前者按照射野要求的强度分布进行分割，利用多叶光栅(multileaf collimator，MLC)形成的多个子野进行分布照射，其特征是在每个子野照射完毕后切断照射，并将MLC调到另一个子野位置，继续照射，直到所有子野照射完毕，将所有子野的流强相加，即可形成要求的强度分布［1-2］.后者则利用多叶光栅相对应的一对叶片的相对运动，实现对射野强度的调节，其特征是叶片运动过程中，射线一直处于“Beam on”的位置，剂量率不变［2］.与动态调强模式相比，静态调强模式具有硬件实施容易控制、可靠性高等优点［3-4］.前期研究在对比了2种调强模式后认为，静态调强模式在降低正常器官受照射剂量方面优于动态调强模式［5］.因此，本文主要研究静态调强模式中的多叶准直器射野分割算法.

在静态模式中，过多的总子野个数 (total number of segments)将延长治疗时间，过多的总机器跳数(total number of monitor units)将增加叶片间的射线泄露.因此，如何在保证投射剂量的前提下减少总子野个数和总机器跳数是优化子野分割的两大目标［6］.与此同时，为了减少叶片间的凸凹槽效应、提高射线的利用率，在满足上述目标的基础上，子野的开口面积也应设计得尽可能大.

本文主要考虑的是相邻叶片允许交叠情况下子野个数最少的射野分割算法.针对这类射野分割问题，目前的解决方法主要是自适应算法［7-9］和规划类算法［10-11］.但对于大规模的矩阵分割，这些方法会影响计算速度.在Luan算法中，首先得到不同的多叶准直器开口形状和机器跳数对，然后将每行中不同多叶准直器的开口形状整合成相应的子野，在保证每行MLC开口最大的情况下减少子野个数［12］.Engel算法是一种自适应算法，在控制总机器跳数的同时，所需的子野个数几乎最少［7］.本文结合Engel算法所需较少总子野个数的优点，对Luan算法进行改进.改进后的算法在保证每行中准直器开口最大的同时，减少了所需子野个数和总机器跳数，且所需计算量较Engel算法更少.

1 算法描述

将m×n的二维矩阵A用于描述来自于放疗逆向计划的射野强度图.A可被分割为包含不同机器跳数的子野，即

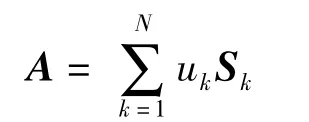
式中，N为总子野个数;uk＞0为第k个子野的强度值;Sk为第k个子野的形状，其元素由0，1构成，分别表示该位置已被、未被MLC遮挡，且每一行中的所有1必须连续.Sk中元素的值由该子野中每行MLC左、右叶片的位置li，ri决定，即

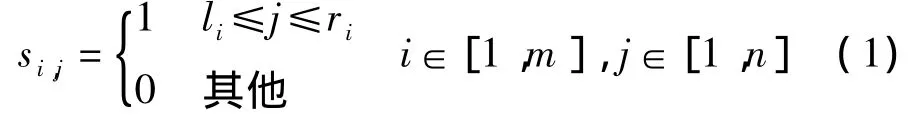
例如，矩阵A被分割为4个子野，总机器跳数为5+2+1+1=8，则A可以表述为

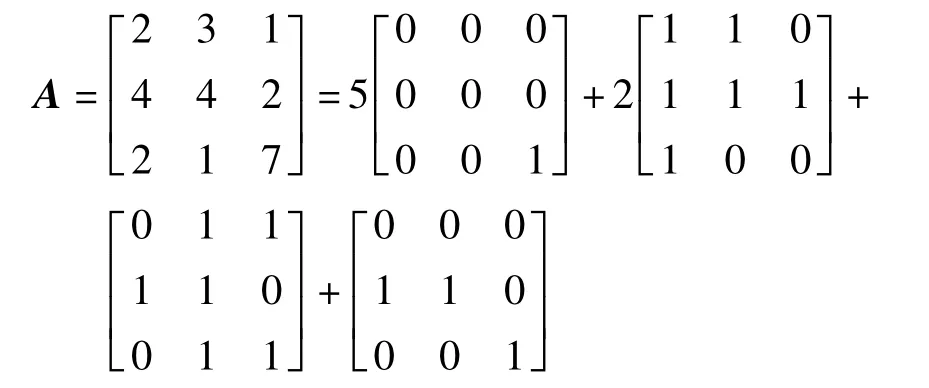
本文只考虑相邻叶片允许交叠情况下的射野分割算法.为了描述方便，在矩阵A中加入2列零元素，即

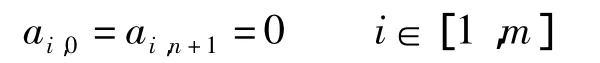
并定义其m×(n+1)维横向差分矩阵D，其中元素表示为

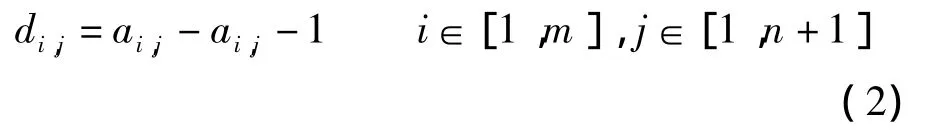
矩阵A中第i行机器跳数复杂度定义为

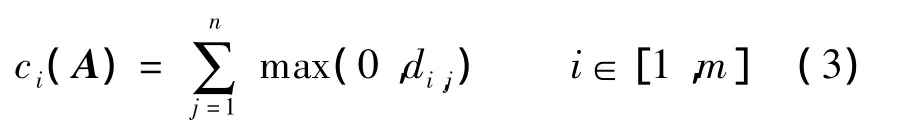
矩阵A的机器跳数复杂度为所有行中机器跳数复杂度的最大值，即

第i行的复杂度间隔为

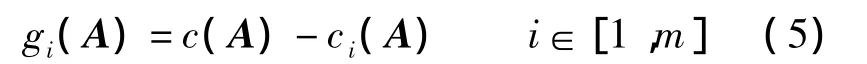
1.1 Luan 算法

在保证每行MLC开口最大的情况下，可利用Luan算法来减少子野个数.算法的具体步骤如下.

①将矩阵A按行分割成m个行向量Xj，其中j∈［1，m］.

②将每一个行向量Xj分割成多个MLC开口形状和机器跳数对(Sj，i，vj，i)，并将机器跳数值 vj，i以∑ai2i的形式分割成多个MLC形状和机器跳数对(Sj，i，20)，(Sj，i，21)，(Sj，i，22)，…，(Sj，i，2m).例如，可将(Sj，i，5)分割为(Sj，i，21)，(Sj，i，22).然后，将分割后的MLC开口形状和机器跳数对(Sj，i，v)按机器跳数值重新排序为(Sj，i，vj，i).

③将每行不同的MLC形状整合成相应的子野.算法描述如下:

Biedl等［13-14］将该算法扩展为按 ∑ai3i和∑ai4i的指数和形式分割，以进一步减少子野个数.

1.2 Engel算法

在保证总机器跳数最小的情况下，利用Engle算法可以得到近似最优的子野个数.当矩阵A的复杂度为0时，射野分割结束.该算法中，为了减少子野个数，每次分割时尽可能取大的机器跳数值uk，以尽可能多地减少矩阵A的复杂度，即

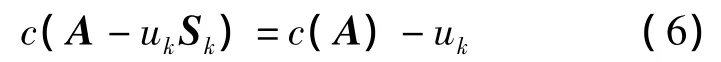
式(6)中，uk取值为所有行中机器跳数值u'k的最小值，u'k为每一行任意准直器叶片处最大可取的机器跳数值.对于机器跳数复杂度最大行，任意准直器叶片位置处u'k的取值须满足以下条件:

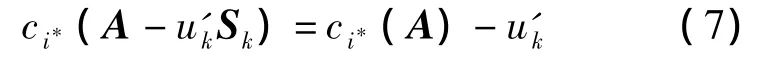
式中，i*表示机器跳数复杂度最大行.

对于其他行，u'k的取值要满足该次射野分割后该行机器跳数复杂度不大于机器跳数复杂度最大行的复杂度，即

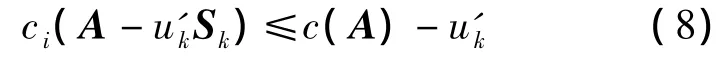
每次射野分割后，第i行的机器跳数复杂度为

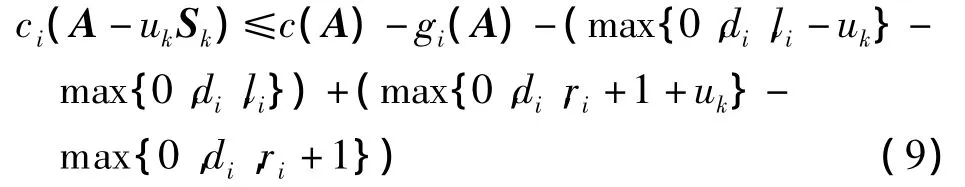
式(9)可以变换为

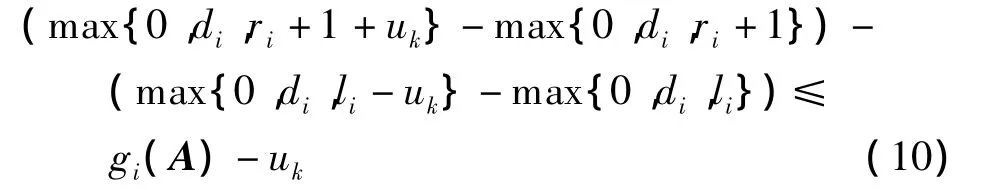
根据每行中左、右叶片处的强度差分值，可以分以下2种情况来确定第i行中的最大机器跳数取值 ki(r，l):

1)当该行准直器开口为空时，则

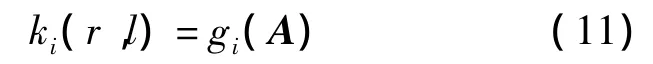
2)当该行准直器开口非空时，则

① 若 ki(r，l)≤min{di，li，－ di，ri+1}，则不等式(10)恒成立;

② 若 min{di，li，－ di，ri+1}≤ki(r，l)≤max{di，li，－ di，ri+1}，则

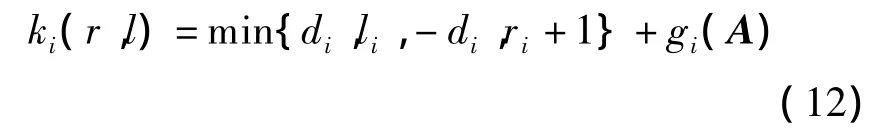
③ 若 ki(r，l)≥max{di，li，－ di，ri+1}，则

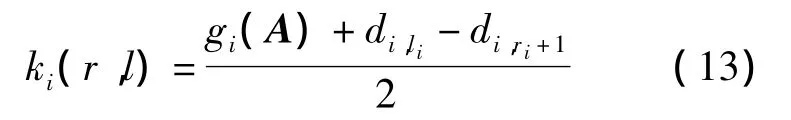
为了保证分割后矩阵A中所有元素非负，每行中的最大机器跳数值ki(r，l)应小于等于矩阵A中所有元素的最小值.第i行中准直器开口内矩阵A中所有元素的最小值为

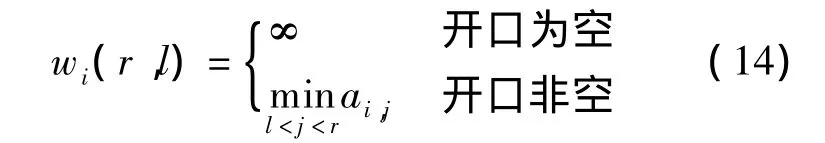
当前行中最大允许的机器跳数取值为

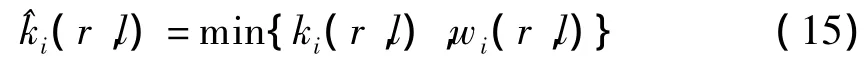
矩阵A中最大允许的机器跳数取值为

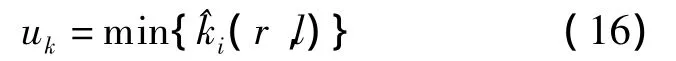
已知矩阵A中最大允许的机器跳数取值uk后，可根据子野开口面积最大、总机器跳数最小、子野开口面和对应机器跳数的乘积最大等不同准则来确定对应MLC开口形状Sk.Engle算法在减少子野个数的同时，增加了部分行的复杂度，而且在这些行中生成的MLC开口都较小.

1.3 改进算法

Luan算法和Biedl等［13-14］提出的改进算法都存在一个共同的问题，即对某些数值的处理反而导致子野个数增加.例如，当前子野的机器跳数为7时，如果按∑ai2i形式进行分次照射，该子野应该继续分割为机器跳数分别为4，2，1的3个子野，与直接按机器跳数7进行照射相比，增加了2个子野.为此，本文结合Engel算法的优点，对Luan算法提出进一步改进.改进算法的具体步骤如下.

①将矩阵A按行分割成m个行向量Xj，其中j∈［1，m］.

②将每一个行向量Xj分割成若干个MLC开口形状和机器跳数对(Sj，i，vj，i).

③将每行不同的MLC开口形状整合成相应的子野.算法描述如下:

与Engel算法相比，改进算法在减少子野个数的同时，尽可能保证了每行的MLC开口面积最大.与Luan算法相比，改进算法不再受指数函数的限制，减少了部分不必要增加的子野，降低了子野数，而且没有增加机器总跳数.

2 实验结果

利用本文算法对1 000个15×15不同最大射野强度的随机矩阵进行分割，并将结果与经典的Bortfeld 算法［6］、Xia 算法［4］、Engel算法以及 Luan算法得到的结果进行比较(见表1).表1中，T表示1 000个随机矩阵的平均总子野个数;M表示平均总机器跳数;L表示随机矩阵的最大值.由表可知，与Luan算法相比，本文算法在减少子野个数的同时，降低了总机器跳数;与Engel算法相比，本文算法没有增加总机器跳数，仅平均增加了1个子野.究其原因，Engel算法为了保证在每次分割中尽可能多地减少强度矩阵的复杂度，增加了部分行的子野个数，而且增加的这些子野的MLC开口都比较小;而本文算法在进行分割的时候，为了确保每行中的MLC开口尽量大，减小了对应的机器跳数值，因而增加了总子野个数.

射野分割算法的运行时间与强度矩阵的大小以及每个像素的强度值有关.矩阵和强度值越大，所需分割时间越长.根据实际准直叶片对数(如美国Varian公司用于常规放疗的MLC叶片对数有26，40或60对)，对最大强度值为26、大小为26×26，40×40和60×60的随机矩阵的分割时间进行比较.在内存为2 GB的双核英特尔酷睿台式机上运行Engel算法、Luan算法及本文算法，结果见表2.由表可知，与Engel算法相比，本文算法和Luan算法所需计算时间较短.而且随着矩阵的变大，本文算法在缩短计算时间上的优势更加明显.

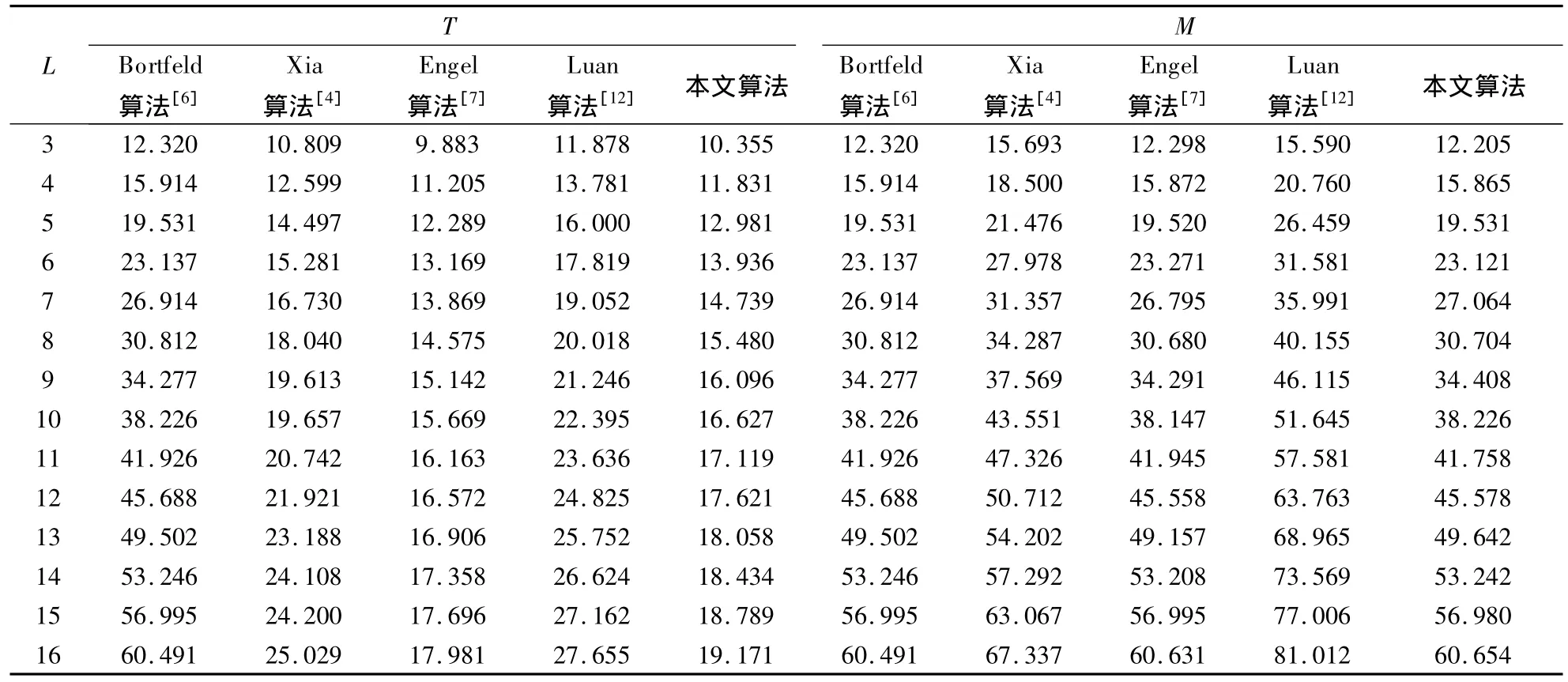
表1 本文算法与经典算法的计算结果比较

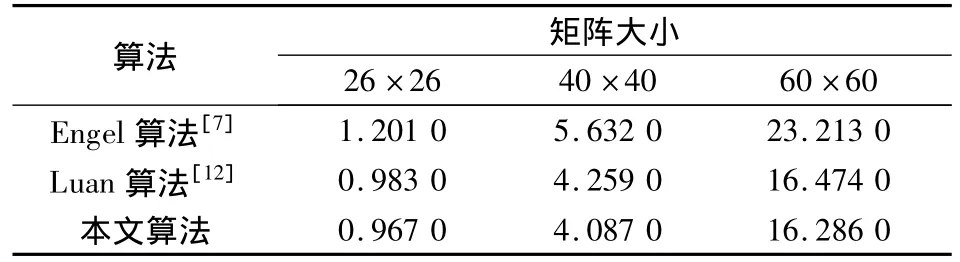
表2 本文算法与经典算法的计算时间比较 s

3 结语

本文通过结合Engel算法的优点，对Luan算法进行了改进.改进后的算法不再受指数函数的限制，进一步减少了射野分割所需的子野个数.与传统算法相比，本文算法能在减少子野个数和机器总跳数的同时，保证每行中准直器的开口最大.与Engel算法相比，本文算法所需计算量更小.

考虑到临床实际需求，IMRT计划产生的强度矩阵远大于15×15，由此带来的时间和剂量学上的优势将更为显著.影像引导放射治疗的广泛应用需要在患者不离开治疗床的情况下在线快速修改及重新优化放疗计划，这也为本文算法提供了广阔的发展空间和良好的应用前景.

References)

［1］Boyer A L，Yu C X.Intensity-modulated radiation therapy with dynamic multileaf collimators［J］.Semin Radiat Oncol，1999，9(1):48-59.

［2］胡逸民.肿瘤放射物理学［M］.北京:原子能出版社，1999:550.

［3］Dai J，Zhu Y.Minimizing the number of segments in a delivery sequence for intensity-modulated radiation therapy with multileaf collimator［J］.Med Phys，2001，28(10):2113-2120.

［4］Xia P，Verhey L J.Multileaf collimator leaf sequencing algorithm for intensity modulated beams with multiple static segments［J］.Med Phys，1998，25(8):1424-1434.

［5］朱健，刘敏，李建彬，等.多叶光栅静态调强技术对鼻咽癌放疗中危及器官受量的作用［J］.中华放射医学与防护杂志，2009，26(2):171-173.Zhu Jian，Liu Min，Li Jianbin，et al.The role of the organ at risk in radiotherapy for nasopharyngeal carcinoma using multileaf in collimator static intensity modulated［J］.Chin J Radio Med Prot，2009，26(2):171-173.(in Chinese)

［6］Kalinowski T.Realization of intensity modulated radiation fields using multileaf collimators［C］//Lecture Notes in Computer Science.Berlin:Springer-Verlag，2006，4123:1010-1055.

［7］Engel K.A new algorithm for optimal multileaf collimator field segmentation［J］.Discrete Appl Math，2005，152(1/2/3):35-51.

［8］Kalinowski T.A duality based algorithm for multileaf collimator field segmentation with interleaf collision constraint［J］.Discrete Appl Math，2005，152(1/2/3):52-88.

［9］Siochi R A C.Variable depth recursion algorithm for leaf sequencing［J］.Med Phys，2007，34(2):664-672.

［10］Cambazard H，O'Mahony E，O'Sullivan B.A shortest path-based approach to the multileaf collimator sequencing problem［J］.Discrete Appl Math，2012，160(1/2):81-99.

［11］Taskin Z，Smith J，Romeijn H，et al.Optimal multileaf collimator leaf sequencing in IMRT treatment planning［J］.Operations Research，2010，58(3):674-690.

［12］Luan S，Saia J，Young M.Approximation algorithms for minimizing segments in radiation therapy［J］.Information Processing Letters，2007，101(6):239-244.

［13］Biedl T，Durocher S，Hoos H.et al.A note on improving the performance of approximation algorithms for radiation therapy［J］.Information Processing Letters，2011，111(7):326-333.

［14］Biedl T，Durocher S，Engelbeen C，et al.Faster optimal algorithms for segment minimization with small maximal value［C］//Proceedings of the 12th International Conference on Algorithms and Data Structures.New York，USA，2011:86-97.