一种改进的正弦灰度变换图像增强算法

龚昌来，罗 聪，杨冬涛

(嘉应学院电子信息工程学院，广东 梅州 514015)

图像增强是图像处理中的一个重要领域，它的目的是突出图像中需要的信息，削弱或消除不需要的信息，增加图像中不同物体特征之间的灰度差异，以改善图像的视觉效果。

图像增强方法很多，如直方图均衡化、灰度变换法、基于小波变换法［1－2］等。对于数字视频图像的增强处理，除要求图像增强效果好之外，还要求处理速度快，满足实时性的要求。灰度变换法是一种最简单，但却非常有效的空间域对比度增强方法［3－4］，它通过对像素灰度的直接伸缩实现对比度扩展，具有运算量小、处理速度快的特点。灰度变换可分为两种类型:线性和非线性变换。非线性变换的增强效果一般优于线性变换，但存在确定变换函数困难、通用性差的缺陷。

正弦灰度变换是一种非线性变换，它通过调整正弦函数曲线形状参数，可实现如对数、指数函数等多种非线性灰度变换［5］，具有变换曲线非常灵活、算法简单的特点。近年来，一些学者将正弦灰度变换应用于图像增强，并取得一些成果［6－7］。但是，经典的正弦灰度变换在图像增强应用中存在一些问题，如灰度伸缩的拐点及伸缩强度参数相互影响，不能独立可控，会导致部分灰度区域无法实现伸缩，而且不能够结合图像灰度特征进行针对性增强［8］。本文介绍一种改进的正弦灰度变换图像增强方法，提出一种新的非线性S形状灰度映射曲线，灰度伸缩的拐点及伸缩强度均可控制，可有效地提高图像的增强效果，并且计算简单、处理速度快。

1 正弦灰度变换

灰度变换是将原图像的灰度函数f(x，y)经过一个变换函数T变换成一个新的图像函数g(x，y)，即

由式(2)可知，正弦灰度变换有5个可选参数，分别为 a，b，c，d，k。其中 a，b，c，d 的作用同线性灰度变换一样，用于调整拐点的位置及各部分的斜率;k为指数因子，用于调整正弦曲线的形状，从而实现对指定灰度区域的扩展或压缩。图1为式(2)的波形图。

图1 经典正弦变换曲线

由图1可知:

1)当k＜2时，正弦灰度变换对整个［a，b］范围内灰度均进行扩展，并且k越小，越接近于对数灰度变换;

2)当k＞2时，正弦灰度变换扩展高灰度区域［q2，b］，压缩低灰度区域［a，q2］，并且 k越大，越接近于指数灰度变换;

3) 当k=2时，扩展高灰度区域［q1，b］，压缩低灰度区域［a，q1］，并且 q1为［a，b］的中点。

由以上3点可知，只需调节参数，即可调整正弦函数曲线形状，实现诸如对数、指数函数等多种非线性灰度变换。正弦灰度变换虽然非常灵活，但存在以下问题:

1)拐点(即扩展与压缩的分界点)不能独立选择。若a，b，c，d参数确定后，拐点位置也随之确定。图1中，k＜2时无拐点;k=2时，拐点q1为［a，b］区间的中点;k＞2时，由计算可知，拐点 q2与 a，b，c，d，k 参数有关。已知灰度变换增强图像的本质是通过对像素灰度的扩展或压缩实现的，对拐点的选择非常重要，若拐点选择不恰当，会造成错误的操作，即对本应压缩的灰度进行扩展，而对本应扩展的灰度进行压缩。理想的拐点选择，应独立可控，并由原始图像f(x，y)的灰度分布决定。

2)在式(2)中，指数因子k不仅影响变换曲线的斜率，还影响变换曲线形状和拐点位置。造成灰度伸缩强度不能独立调整，难以获得与原始图像f(x，y)的灰度分布特征相适应的变换曲线，所以，不能获得较好的增强效果。

2 改进的正弦灰度变换及参数选择

2.1 改进的正弦灰度变换

针对经典正弦灰度变换在图像增强中存在的问题，本文对其进行改进，改进后的正弦灰度变换数学表达式为

式(3)的波形图如图2所示。

改进后的正弦灰度变换特点是:1)变换曲线由两段正弦曲线组成，呈S形状，其导数是光滑的，灰度伸缩性能好;2)灰度伸缩的拐点q及伸缩强度k均可控制，应用灵活方便，通用性强。k值的范围为k≥0:k=0时，g(x，y)=f(x，y)，无增强作用;k值增大时，对灰度的伸缩强度增大，增强效果加强。

图2 改进的正弦变换曲线

改进后的正弦灰度变换存在的问题是变换后图像灰度动态范围与变换前相同均为［a，b］。为了扩展增强图像灰度动态范围，可先将原始图像f(x，y)的灰度动态范围采用式(4)进行线性拉伸，将其灰度动态范围扩大到与显示设备动态范围一致，再按式(3)进行增强处理。

式中，fmax，fmin为图像f(x，y)的最大和最小灰度值。线性拉伸后图像 f'(x，y) 的灰度动态范围为［c，d］，对8 bit图像，动态范围［c，d］取［0，255］;对10 bit图像，［c，d］取［0，1023］。

2.2 拐点q的选择

一幅图像的信息可划分为目标区域和背景区域两部分，阈值法是一种简单有效的图像目标与背景分割方法。本文釆用图像的全局分割阈值作为拐点q的参数值，该选取方法的灰度伸缩策略是:对于灰度值高于阈值的目标(或背景)灰度进行扩展，对于低于阈值的背景(或目标)灰度进行压缩，实现提高对比度的目的。图像的分割阈值计算方法很多，如直方图法、熵阈值法、最大类间方差法(Ostu法)、模糊聚类法等［9］，这些方法虽然能比较准确计算出分割阈值，但计算量较大，不能满足图像实时处理的要求。本文采用图像的平均灰度值作为分割阈值，计算量小。

2.3 伸缩强度k的选择

式(3)中k是调节变换曲线各部分的斜率即灰度伸缩强度的参数，为了获得较好的增强效果，k值应根据原始图像的局部灰度分布特征进行选择。本文基于图像局部对比度来确定k值。

假设像素f(xi，yi)是窗口Wi的中心点，其邻域像素的数目为m，像素f(xi，yi)的局部对比度定义为［10］

式中，α为正常数。α值增大，图像全局增强度增大，反之亦然。实验结果表明，α一般在10～40范围中选取。

本文采用基于图像局部对比度的方法确定k值，其策略是:当某像素的局部对比度较大时，表明该像素处于边缘细节区域，此时应增加k值，加大灰度伸缩强度，以利于增强边缘细节信息;反之，局部对比度较小时，表明该像素处于平坦区域，此时灰度伸缩强度应减弱，以免增加多余的信息，破坏区域的平坦性。因此，该策略具有对边缘细节信息增强能力强而对平坦区域信息破坏少的特点。

2.4 算法步骤

本文方法的算法步骤如下:

1)输入待增强图像f(x，y);

2)按式(4)对f(x，y)进行线性变换，得到灰度动态范围扩展图像f'(x，y);

3)计算图像f'(x，y)的灰度平均值作为拐点q的值;

4)选择合适的α值，对图像f'(x，y)的每一个像素点，先取一个3×3(或5×5)邻域，按式(5)～(7)计算伸缩系数k，再代入式(3)计算，将计算结果作为增强图像g(x，y)对应像素点的灰度值。

3 实验结果与分析

为验证本文算法的有效性，将本文算法与经典正弦变换增强方法和传统的直方图均衡化方法进行增强效果对比实验。选用Lena(256×256)，Peppers(256×256)两幅图像作为测试图像。先采用5×5均值滤波模板对测试图像进行平滑处理来模拟模糊受损降质图像，然后采用3种方法对降质图像进行增强运算。增强效果的定量评价指标采用峰值信噪比(PSNR)、信息熵(Entropy，ENT)和平均梯度(Average Gradient，AG)。

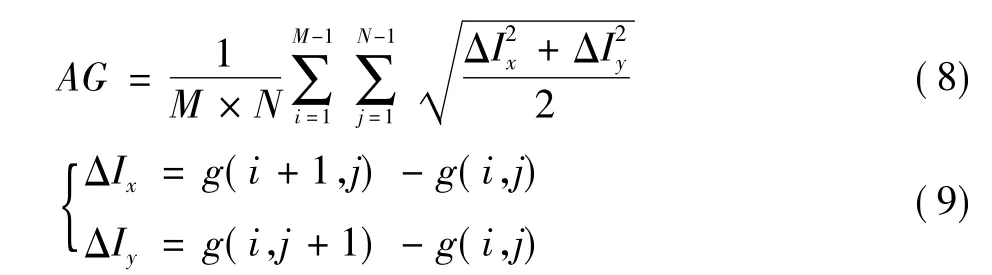
式中:M，N分别是图像g的长和宽。峰值信噪比反映增强图像与原图的逼近程度，峰值信噪比大表示增强图像逼近原图像，失真程度小，图像质量好; 信息熵是衡量图像信息丰富程度的一个指标，其值越大，表示图像所含信息量越大;平均梯度反映了图像中微小细节反差与纹理变化特征及清晰度［11］，平均梯度越大表示增强图像清晰度越高，增强效果越好。

由于本文算法及经典正弦变换法的增强效果与各自参数有关，所以取最佳增强效果时的图像和性能评价指标值进行比较。3种算法的增强效果图像见图3、图4，性能评价指标数据见表1。

在主观视觉上，由图3、图4可见，直方图均衡化处理的图像，对比度大，但亮度偏亮，图像细节欠丰富;经典正弦变换增强算法的图像质量优于直方图均衡法，但清晰度不高;本文算法的图像细节丰富，清晰度高，与原图像比较逼近，增强图像的主观视觉效果优于其他两种方法。

表1 性能评价指标数据

在客观评价上，由表1可知，直方图均衡化处理的图像PSNR，AG和ENT值较小，表明增强图像失真程度大，图像增强效果差;经典正弦变换法增强图像的各项性能评价指标值略优于直方图均衡法。本文算法增强图像的AG和ENT值略优于经典正弦变换法，但PSNR值明显优于经典正弦变换法，提高约3 dB。实验结果从主观视觉和客观评价上都表明本文算法的增强效果优于其他两种方法。

4 结论

为了提高图像增强效果，本文对传统的正弦灰度变换进行改进，提出一种新的变换函数模型，它是由两段正弦曲线构造的S形变换曲线，灰度伸缩的拐点及伸缩强度参数独立可调，并根据图像的灰度分布自适应选择。实验结果证明本文算法较经典正弦变换法和直方图均衡法增强效果好，具有增强图像失真度小、对边缘细节信息增强能力强而对平坦区域信息破坏少等特点。并且计算简单、运算速度快、易于实现(正弦函数是基本函数，在专用芯片上易于实现)，可用于数字视频图像的实时增强处理。

［1］曾鹏鑫，么健石，陈鹏，等.基于小波变换的图像增强算法［J］.东北大学学报:自然科学版，2005，26(6):527－530.

［2］王海峰，吴冬燕，章怡.一种小波变换的小波系数均衡图像增强算法［J］.电视技术，2011，35(19):27－29.

［3］PELI E.Contrast in complex images［J］.Journal of Optical Society of A-merica A，1990，17(10):2032－2040.

［4］AMPAZIS N，PERANTONIS S J.Two highly efficient second－order algorithms for training feed forwards networks［J］.IEEE Trans.Neural Networks，2002，13(5):1064－1074.

［5］杨词银，黄廉卿.基于正弦灰度变换的X光图像增强［J］.光学技术，2002，28(5):407－408.

［6］汪家旺，胡益斌，张维林.X线图像正弦灰度变换增强技术临床应用研究［J］.放射学实践，2007，22(2):211－212.

［7］冯清枝，王明灿，周纯冰.非线性灰度变换在图像增强中的运用［J］.中国刑警学院学报，2008(2):59－61.

［8］寇小明，刘上乾，洪鸣，等.一种自适应红外图像增强技术［J］.西安电子科技大学学报:自然科学版，2009，36(6):1070－1074.

［9］谢勰，王辉，张雪锋.图像阈值分割技术中的部分和算法综述［J］.西安邮电学院学报，2011，16(3):1－5.

［10］王炜华，沈振康.用局部对比度信息改善图像质量［J］.国防科技大学学报，2003，25(3):58－61.

［11］曾立庆，蒋年德.基于邻域内相关系数与平均梯度的图像融合方法［J］.计算机工程与设计，2010(7):1533－1535.