高性能图像多级小波变换的硬件设计与实现

夏海静，温 彤，李其虎

(1.衡水学院 数学与计算机系，河北 衡水053000;2.上海海事大学 物流工程学院，上海201306;3.中国科学院 光电技术研究所，四川 成都610209)

自从20世纪80年代小波数学理论的诞生到现在，小波理论经历了多个发展阶段，从数学理论的建立和研究，到基于傅里叶分析形成的第一代小波的Mallat卷积算法，直至提升小波思想的引入发展出第二代小波基的构造方法，小波分析以其良好的时间频率分析特征以及多尺度分析能力已经被广泛地应用于图像处理的各个领域［1-2］。针对小波分析实现方式而言，此处单从二维离散小波的数学原理角度出发，可以概括为2种方法:一种方法就是参照一维小波变换结构，构造出二维小波变换基，利用被构造的二维小波基函数直接对图像信号进行分析，从而得出变换结果;另一种方法就是将二维图像信号理解为由多个一维信号组合而成，采用一维信号的小波分析方法来实现数字图像的二维小波变换［3-4］。这种方法简单易实现，进而被广泛采用。关于二维离散小波变换的硬件实现，目前国内外许多学者提出了许多好的结构及其硬件实现方式。例如TAN等人采用第二代提升小波结构，将图像边缘数据内嵌于整个算法过程中，很好地解决了图像数据边界扩展问题［5］。文献［6-7］中采用的原位数据运算方式，利用图像像素在变换过程中变化的特征规律，取得较好的效果。此外也有其他学者针对不同小波变换的硬件实现提出了不同的硬件设计方案［8-9］。

本文从小波分析的数学原理出发，在总结前人的基础上［10-11］，以Le Gall(5/3)小波为例，设计了一种结构异常简单，性能优良的高速图像多级小波变换结构。该结构在图像数据运算过程中充分考虑每个像素的运算特点，在读取二行面阵图像数据之后，整个变换就开始执行。该变换结构最大特点可以概括为:1)在进行二维图像变换时，不需要等所有行(列)变换结束后，再进行列(行)变换;2)不需要某一级变换完成后再进行下一级变换。本文所设计的变换架构可以多级同时变换，进而有效地提高了变换速度，为基于小波分析图像处理技术的高速硬件实现提供了基础。

1 小波分析理论基础

对于给定一个基本函数ψ(t)，令

式中:a和b均为常数，且a＞0。函数ψa，b(t)是基本函数ψ(t)先作移位再作伸缩以后得到。a和b不断地变换，可得到一组函数ψa，b(t)。所以对于给定一个平方可积信号x(t)，即x(t)∈L2(R)，则x(t)的连续小波变换被定义为

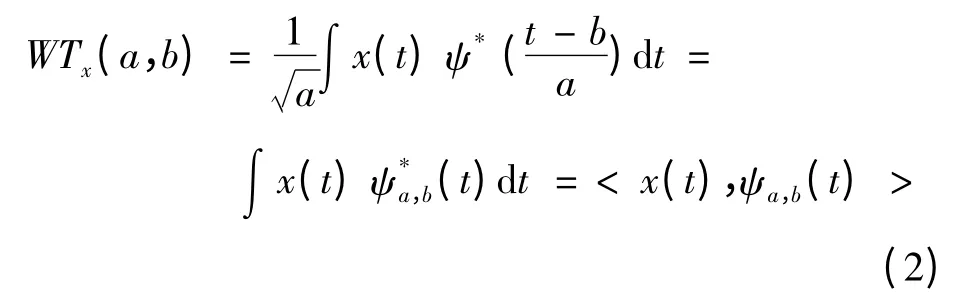
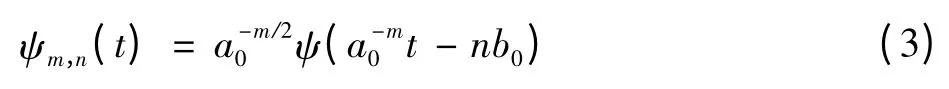
则正变换形式为

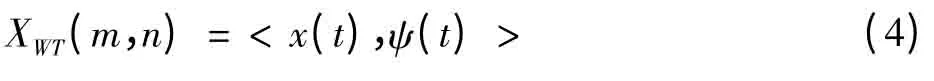
传统的小波变换(第一代小波)采用的都是卷积算法。典型代表为基于滤波器结构的Mallat算法，其过程复杂，用算量大，实时性差，硬件实现困难。目前工程实际进行小波变换的方法是基于提升结构的第二代小波变换。本文中基于VLSI实现的多级小波变换是JPEG2000标准中采用的Le Gall(5/3)小波，其对应的滤波器组的形式为分别代表分析端高通与低通滤波器抽头系数。对于长度为N的一维序列，采用Mallat公式需要2N点乘法运算。利用提升算法，发现只需要N点乘法，即从乘法运算量上即可降低一半。此外通过分析该滤波器变换时的数据特征可以看出，Le Gall(5/3)提升变换过程是典型的同址、原位运算过程。

2 Le Gall(5/3)提升小波原理

Le Gall(5/3)小波正向变换过程的数学表达式为

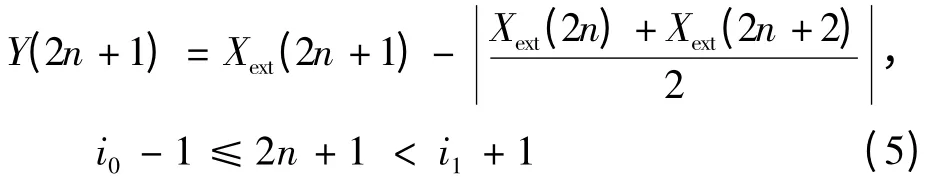
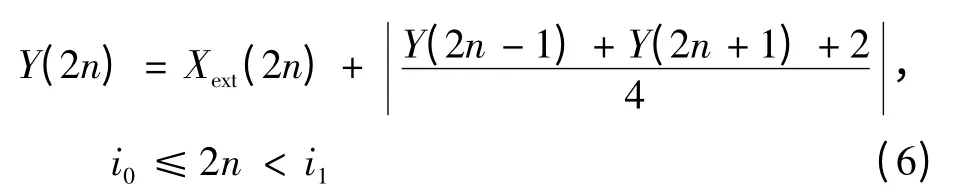
式中:Y是一维信号X的变换结果。其中，Xext(n)是一维信号X的对称周期扩展，i0和i1分别是X第一个样本和最后一个样本的序号。由上一节可知，在进行信号的提升变换过程中，通常要经过分裂、预测和更新这3个步骤。一维Le Gall(5/3)小波提升架构如图1所示，在输入端，将信号进行奇偶分裂，用偶数项来预测奇数项，再用预测后的奇数项来更新偶数项，从而实现一维一级提升。

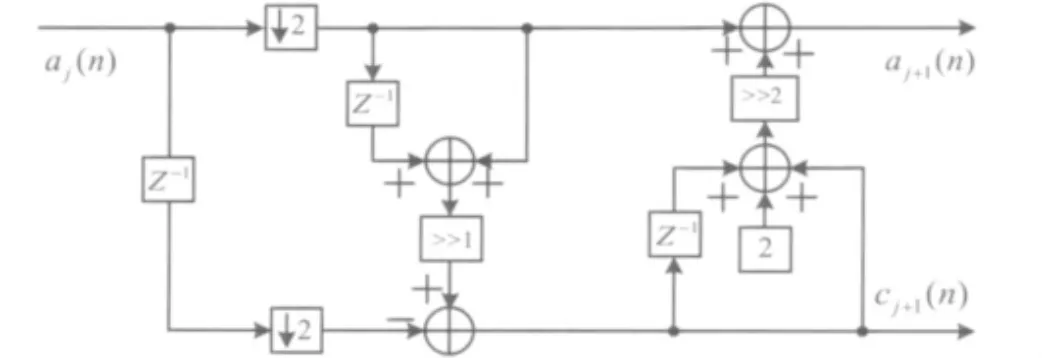
图1 Le Gall(5/3)小波提升硬件实现架构

通过分析(5/3)小波提升架构可知，在提升过程中，分裂仅仅是一个概念，在实际运算过程中并不是必需的。计算过程中只要能确定哪些是奇数项、哪些是偶数项即可。图1中2倍下采样表示将原始信号分解为2个奇数项和偶数项。在硬件实现时，通过奇偶选择信号，将奇偶项分开。奇偶信号分别用不同的信号端口输出，此时时钟频率降为原始数据时钟的一半。将偶数项信号延迟后相加，再经过移位除法器后与相对应的奇数项相减，来预测奇数项值，之后通过延迟环节将得到的2项预测值来更新奇数项。

值得注意的是，在一维信号长度为0～N-1的起始端和结束端运算时，信号要进行边界延拓，上述内容里已经提到多种边界延拓方式，在实际硬件运算过程中，由于传统方法一般采用周期对称拷贝边界数据或是通过地址转换将延拓部分数据映射到原始数据上。这2种方法需求内存较多，且功耗较大。为此本设计在结构上采用了改进的内嵌延拓提升［5］方法以解决边界周期延拓问题，具体做法为:当判断信号为最左端起始信号时，对x(0)进行更新操作，由于缺乏左边预测项，所以此时的更新公式变为式(7);当判断信号为最右边时，对x(N-1)进行预测操作，由于缺乏右边的预测项，则此时的预测公式变为式(8)。其他情况下，由于不需要进行数据延拓，则按照正常提升方式进行。内嵌延拓提升将原来统一计算流程分成3个阶段，分别为起始阶段、长时间正常运行阶段和结束阶段，所以在变换时需要加一个计数器以判断一行的起始和末尾。针对二维图像信号还需要加上一个计数器来判断起始行和末尾行。式(7)和式(8)为

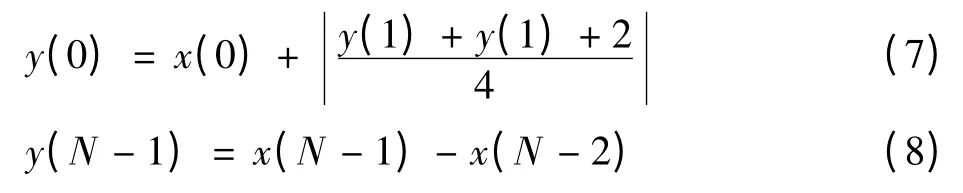
3 二维提升小波变换的硬件实现

3.1 一级二维小波提升硬件实现

为检验上述设计思想的正确性，在Xilinx公司的ISE10.1.3开发环境下，采用VHDL语言开发了上述一维5/3整数小波正向变换过程。为便于层次化设计，结构采用模块化设计，其模块接口如图2所示。输入端口包括输入数据Data_in、输入数据有效性In_valid、输入数据时钟频率Clock_in、输入数据的二分频时钟Clock_in/2，以及整个模块的复位信号Reset。输出端口包括低频信号输出部分Data_L、高频信号输出部分Data_H以及输出信号是否为效信号Out_valid。

图2 1D Le Gall 5/3小波变换外围接口图

为证明该结构的功能正确性，图3为该结构对一组长度为12的一维信号进行一级变换后，得到的输入输出数据值。从波形图中可以看出，从原始数据输入到输出需要经过10个时钟周期的延迟。在Xilinx公司的XC5VFX70T(-3)型号FPGA下进行综合时钟频率高达399.76 MHz。该结构的正确、高效设计为高速二维图像信号的小波变换的硬件实现做好了前期准备。

图3 软件功能仿真5/3小波变换波形图

在对分辨力为M×N图像进行二维小波硬件提升时，图像以偶数行开始，奇数行结束，在第0行和第M-1行时，由于缺少前一行缓存数据对偶数行进行更新，缺少第M行对第M-1行进行预测，所以列变换时，同样进行列变换内嵌延拓。当对第0行进行更新时，更新公式表示为式(9)，当对最后一行进行预测时，采用式(10)进行预测。式(9)和式(10)为

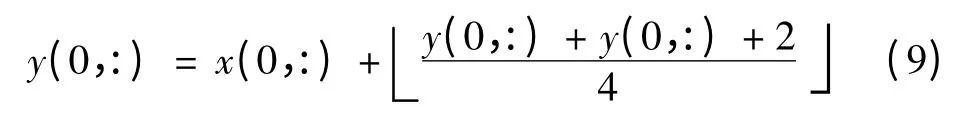
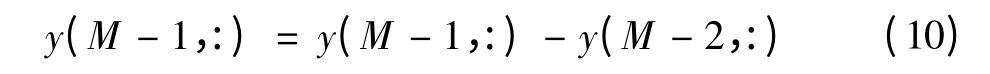
为便于层次化设计，二维5/3小波变换硬件结构同样采用了模块化设计，其模块接口如图4所示，与一维变换模块不同的是，输入端采用帧信号与行信号来决定输入端数据Data_in是否有效。输出端共有6个输出端口，每一个子带都分别对应一个输出信号，分别为LL_T，LH_T，HL_T和HH_T。另外输出端利用输出帧有效性信号Fval_out和输出行有效信号Lavl_out来决定输出信号是否有效。

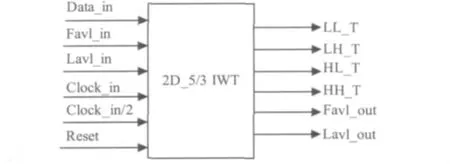
图4 2D 5/3小波变换外围接口图

为验证上述架构的正确性，在Xilinx公司的XC5VFX70T(-3)型号FPGA中，开发上述二维小波提升架构，最终综合后时钟频率可达387.597 MHz，为检验硬件变换后的结果与理论值是否一致，在FPGA中通过模拟一幅二维图像，图像每行都是0～399共400个数据，将模拟的图像数据输入到二维5/3变换模块，输出值通过Chipscope进行数据观察，输出波形图如图5所示，完全符合理论计算值，进而进一步验证了本结构设计的正确性。

图5 一级二维5/3小波VLSI变换波形

3.2 多级二维小波变换的硬件实现

本文中所提的多级二维小波变换同样是采用级联单级二维小波变换模块来实现，级联的单级模块为3.1节中所设计的模块结构。具体按照式(11)进行步步级联从而实现多级变换。

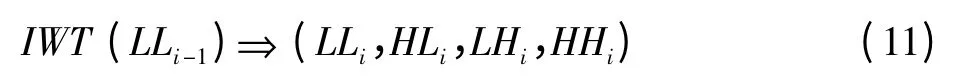
不同变换级与级之间递归级联结构如图6所示。某一级变换后的数据都需要存入一个FIFO，该FIFO的长度至少为下一级变换的一行数据长度。当某一级变换的最低频数据存满一个FIFO后，控制程序会将该FIFO中的数据顺序读出，送入下一级变换模块，并相应的输出4个子带。值得注意的是，该结构不同变换级之间采用FIFO进行缓存后再输入到下一个变换模块中，而不是将某一级最低频子带有数据就送入下一级中。这样做的目的主要有:1)使得整个多级变换模块的流水线更短，硬件变换效率更高;2)使得整个多级变换模块时钟同步，所有模块都使用相同的时钟去控制，进而使得整个模块控制起来更加简单。

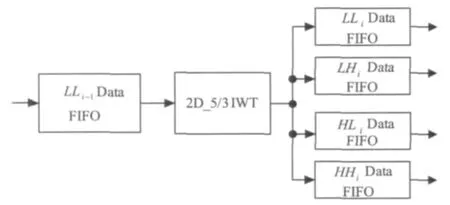
图6 不同变换级之间结构

二维多级变换硬件设计时，系统共有2种时钟，其中一种时钟是图像像素的输入时钟Clock，当每行的数据值从外部输入到内部之后，首先经过分裂器将数据的奇偶分裂开，这时1行数据相当于2行数据，而每行的数据输入频率为原始数据输入频率的一半，即Clock/2，之后这2行数据分别经过预测器和更新器所需要的时钟频率都为原始数据时钟频率的一半。最后的数据输出到外部各自的FIFO中的写时钟都为Clock/2。此外由于每级变换后的数据都有延迟，所以每一级的输出数据除了具有4个子带数据之外，还需要有输出的帧信号与行信号，以便给下一级变换模块使用。当一帧数据变换完成后，系统需要进行复位操作。此外通过分析可知，整个硬件系统中没有任何关于数据地址的操作，即只对变换数据进行移位和存储，从而使得整个系统变得更加简单、易操作。

基于不同变换级结构，以及在前面的二维变换模块的基础，笔者设计了多级二维小波变换的级联递归总体结构框架，如图7所示，该架构可以为实现任何级数小波变换提供硬件架构基础。图中共级联了N个单级二维小波变换递归单元。每一个级联单元虽然都工作在同一个时钟频率下，但是每一级内部又都具有各自的独立性。每一单级小波变换后的数据输出都是连接到各自的FIFO中，除某些低频小波子带FIFO输出端口接到下一级变换码块中以外，所有的子带FIFO输出端都连接到一个多路数据选择器中，多路选择器根据每一级小波子带系数的出现规律，有规则地将各级各子带的小波子带系数输出到后端，供后续图像处理或传输使用。

本文基于上述多级二维小波变换级联递归总体结构框架，对各个模块采用VHDL语言进行程序化设计。利用2款Xilinx公司不同型号FPGA，分别为XC2VP30-FF1152(-6)和XC5VFX70T-FF1136(-3)，进行实际测试，三级二维5/3小波变换在不同器件下资源消耗比例以及综合后时钟频率值如表1所示。从表中可以看出在XC2VP30-FF1152(-6)中，FPGA数据吞吐率能达183 Msymbol/s(兆符号/秒)。利用XC5VFX70T-FF1136(-3)可实现387 Msymbol/s数据吞吐率，而资源消耗最多的内部BRAM则仅仅为整个硬件资源的10%。

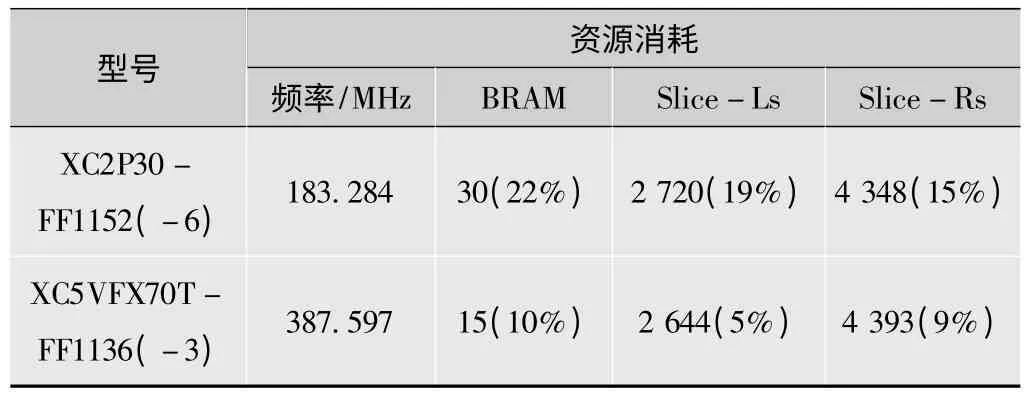
表1 2款硬件资源消耗比例表

4 总结

本文在研究小波分析的数学原理基础上，以Le Gall(5/3)小波为例，分析该小波在进行二维图像提升变换时，每个像素值的运算规律，设计并实现了一种高性能的多级二维小波变换，该小波在对图像进行多级变换时硬件最大的特点有:1)不需要进行传统的行变换之后，再进行列变换，而是采取了行、列同时变换的方式进行;2)在多级变换时，传统变换模式是一级变换完成后才能变换下一级，本文采用的是不同级之间同时变换的方式。最后在硬件电路中，利用VHDL语言完成整个变换架构的设计。实验结果证实本文所设计的多级二维小波变换的硬件实现方式符合理论计算值，从而为基于小波分析的图像处理技术高速硬件实现奠定了基础，具有较高的理论意义与工程应用价值。

［1］SWELDENS W.The lifting scheme:a construction of second generation wavelets［J］.SIAM Journal on Mathematical Analysis，1997，29(2):511-546.

［2］JIANG W，ORTEGA A.Lifting factorization based discrete wavelet transform architecture design［J］.IEEE Trans.Circuits and Systems of Video Technology，2001，11(5):651-657.

［3］DAUBECHIES I.The wavelet transform，time-frequency localization and signal analysis［J］.IEEE Trans.Information Theory，1990，36(5):991-1006.

［4］MALLAT S G.A theory for multiresolution signal decompostion:the wavelet representation［J］.IEEE Trans.PAMI，1989，11(7):673-693.

［5］TAN K C B.Low power embedded extension algorithm for lifting based discrete wavelet transform in JPEG 2000［J］.Electronics Letters，2001，37(25):1328-1330.

［6］颜学龙，余君.二维离散小波变换的FPGA实现［J］.电视技术，2007，31(4):19-21.

［7］康志伟，颜福权.基于提升算法的二维DWT高效VLSI实现结构［J］.国防科技大学学报，2005，27(6):48-52.

［8］林路音.JPEG2000中提升小波算法的FPGA实现［D］.哈尔滨:哈尔滨工业大学，2006.

［9］LIAO H，MANDAL M K，COCKURN B F.Efficient architectures for 1-D and 2-D lifting based wavelet transform［J］.IEEE Trans.Signal Processing，2004，52(5):1315-1326.

［10］ANDRA K，CHAKRABARTI C，ACHARYA T.A VLSI architecture for lifting-based forward and inverse wavelet transform［J］.IEEE Trans.Signal Processing，2002，50(4):966-977.

［11］LINA C J，CHEN K F.Lifting based discrete wavelet transform architecture for JPEG2000［C］//Proc.2001 IEEE International Symposium on Circuits and System(ISIC-2001).Singapore:［s.n.］，2001:497-500.