一种新型模块化多电平换流器调制策略研究

谭玉茹，苏建徽

（合肥工业大学 教育部光伏系统工程研究中心，安徽 合肥 230009）

1 引言

VSC－HVDC的核心部件为电压源换流器（VSC），其拓扑结构有多种形式。两电平或三电平VSC受电平数限制，不能满足更高电压等级和功率等级要求，并且开关管串联均压问题难以解决。模块化多电平换流器（MMC）于2001年首先被提出［1］，其具有以下优点：1）分布式储能电容布置；2）模块化设计；3）简单的串联组合；4）无需大容量交流滤波装置；5）高开关频率；6）易实现冗余；7）良好的前端灵活性；8）使用标准交流变压器或不需变压器；9）共直流总线，适用于高压大功率场合。由于MMC具有以上良好的特性，因而非常适合应用于 VSC－HVDC中［2］。

国内对于MMC的研究近几年才开始，用于VSC－HVDC的MMC电平数往往需要达到几十甚至上百，因此其调制策略的研究成为难点，目前提出的有最近电平逼近调制（NLM）［3］、空间矢量脉宽调制（SVPWM）［4］、多电平消谐波调制（SHPWM）［5］等。

本文根据载波移相脉宽调制（CPS－SVPWM）［6］的思想，在分析了MMC的环流和电容电压均衡问题的基础上，提出了一种新型调制策略，并进行了仿真验证。

2 MMC工作原理

模块化多电平换流器基本结构如图1所示，3个相单元并联形成直流母线，每个相单元包括上、下2个桥臂，每个桥臂由n个子模块（submodule，SM）和1个电抗器L0串联而成。电抗器的作用为提供环流阻抗抑制内部环流和减小故障时的电流上升率。

图1 MMC基本结构图Fig.1 Basic structure of MMC

每个子模块的电路结构相同，如图2所示，由2个IGBT（T1，T2），2个反并联二极管（D1，D2）和1个储能电容组成。

图2 SM电路结构图Fig.2 Schematic diagram of submodule

子模块有3种工作状态［7］：1）T1和 T2均关断时称为闭锁状态；2）T1开通而T2关断时为投入状态；3）T1关断而T2开通时称为切除状态。设桥臂电流为i，子模块电容电压为UCj，输出电压为Uj（1≤j≤2n），子模块在3种工作状态下输出电压情况如表1所示。

表1 子模块工作状态分析Tab.1 Submodule analysisfor different working states

3 MMC环流分析

由于子模块电容分布式布置，各子模块电容电压很难保持平衡，导致3个相单元之间的电压不能完全一致。同时又由于MMC中3个相单元相当于并联在直流侧，因此必然会在MMC的3相桥臂间产生环流，从而使正弦的桥臂电流波形发生畸变。

例文a表示‘我昨天见到了我朋友的哥哥，我很喜欢他’此句中被喜欢的对象是朋友的哥哥。而b则表示‘我昨天见到了一个男生，他是我好朋友的哥哥’此句中被喜欢的对象是‘我’的朋友。

为了方便分析内部环流对MMC的运行产生的影响，图3给出了MMC的一端系统等值电路。Ud为直流侧电压，交流侧可等效为1个交流电压源、1个电阻和1个电感。6个桥臂上的子模块构成的电压可等效为6个受控电压源。

图3 MMC等值电路图Fig.3 Equivalent circuit of MMC

由于三相工作原理相同，下文仅以U相为例进行分析。设iPU，iNU分别表示上、下桥臂电流，iU表示交流侧相电流，icir表示内部环流，其相互关系可由下式表示：

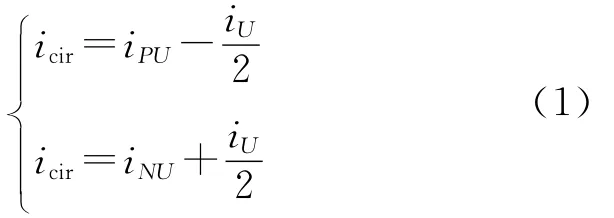
则环流icir为

桥臂上串联的电抗器虽可将环流抑制在较低水平，但仅采用增大电抗器值的方式，只是被动增大了环流阻抗，不可能完全消除环流，并且这种方法在实际工程应用中的成本较高。因此MMC的电容电压均衡控制策略需要考虑环流的因素。

4 MMC电容电压均衡

MMC子模块电容电压均衡控制是MMC控制中的难点，目前提出的方法大多是将子模块电容电压排序，根据桥臂电流方向重新分配子模块触发脉冲序列［8］。本文将子模块电容电压均衡控制分为能量均衡控制和电容均压控制2部分，并给出控制方法。

4.1 能量均衡控制

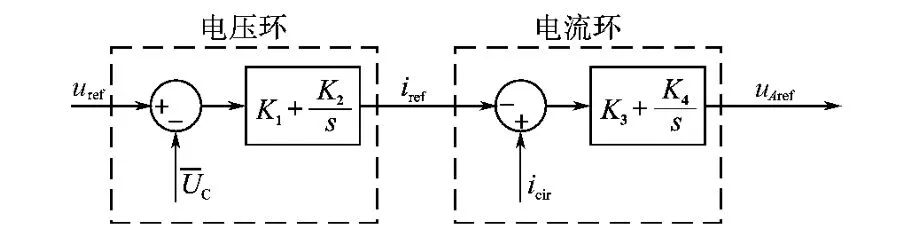
图4 能量均衡控制框图Fig.4 Energy equipartition control block diagram

UCj表示各子模块电容电压，其中1≤j≤2n。其平均值为

电压环控制子模块电容电压的平均值，其输出iref为

电流环控制环流icir，iref作为icir的参考值，输出参考分量uAref为

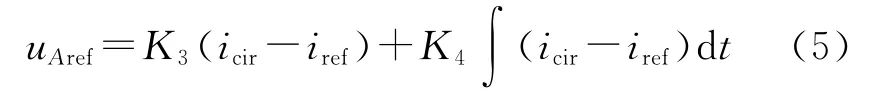
4.2 电容均压控制

电容均压控制的作用是使所有子模块电容电压UCj各自跟踪子模块电容电压参考值uref，保持各子模块电容电压平衡，控制框图如图5所示。

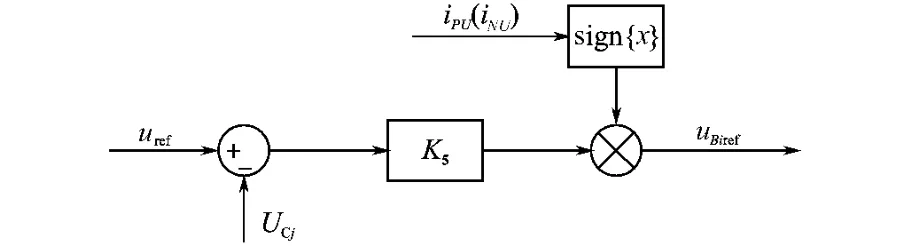
图5 电容均压控制框图Fig.5 Voltage balancing control block diagram

图5中，sign｛x｝表示当x≥0时输出1，x≤0时输出－1。

输出参考分量uBjref的极性由桥臂电流（iPU和iNU）方向决定，当UCj低于uref时，子模块需要从直流侧吸收能量进行充电。若桥臂电流方向为正，uBjref为正的稳压信号，叠加到调制波信号上可增加子模块充电时间。若桥臂电流为负，uBjref为负的稳压信号，叠加到调制波信号上可减小子模块放电时间。

对于上桥臂，uBjref为

对于下桥臂，uBjref为

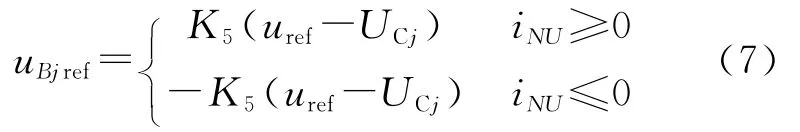
5 MMC调制策略

MMC用于轻型直流输电系统时，所采用的PWM调制策略主要有2大类：基于载波的PWM调制策略和多电平基频开关调制策略［9］。为满足高压大功率的要求，高开关频率会导致较大的开关损耗，从而降低MMC的效率，载波移相脉宽调制策略（CPS－SPWM）可以很好地解决这一问题。本文在上文所述的电容电压均衡控制方法基础上提出了一种新型CPS－SPWM调制策略，与传统的CPS－SPWM相比，不同之处在于调制波中加入了另外的参考分量。因此，该调制策略不仅能实现MMC的多电平电压输出，还能与电容电压均衡策略互相协调。

5.1 三角载波信号

根据CPS－SPWM调制的原理，三角载波信号的数目应等于与一个相单元上的子模块数目2n。由于MMC的直流侧电压由SM的电容电压来承担，为了维持直流侧电压稳定，需要保证每相上、下桥臂处于投入状态的SM个数始终为n。分析可知，每相上、下桥臂的调制策略是对称的，因此上、下桥臂采用相同的n个三角载波信号。n个三角载波信号幅值和频率均相等，相位依次相差2π／n。

5.2 调制波信号

调制波信号与三角载波信号比较，分别控制上、下桥臂子模块投入和切除，调制波信号合成框图如图6所示。

图6 调制波信号合成框图Fig.6 Modulated wave signals synthesis block diagram

uAref为能量均衡控制中所得的参考分量，uBjref为电容均压控制中所得的参考分量。设uU表示交流侧相电压参考值，Ud表示直流侧电压值。

6 仿真验证

本文在Matlab／Simulink环境下搭建了图3所示的MMC模型，对上文提出的调制策略进行了验证。MMC每相由16个子模块构成，上、下桥臂各有8个。仿真参数为：总直流电压Ud＝10kV，子模块电容电压参考值uref＝1.25kV，桥臂电抗值L0＝1mH，调制频率f＝2kHz，调制比m＝0.8。

仿真结果如图7所示，输出电压为良好的正弦波。通过电容均压控制策略，子模块电容电压在参考值附近波动，波动范围在10%以内。

图7 仿真结果Fig.7 Simulation results

7 结论

本文介绍了MMC的拓扑结构和工作原理，分析了MMC的内部环流产生原因，讨论了子模块电容电压均衡问题需要考虑的因素，给出了一种适用于MMC的新型载波移相调制策略及其实现方法。该方法不仅大大降低了换流器的开关损耗，还具有良好的电容电压均衡控制性能。仿真结果验证了所提出调制策略的可行性和有效性。

［1］Marquardt R.Stromrichterschaltungen Mit Verteilten Energiespeichern.German Patent DE 10103031／24.01.2001，Jan.24，2001.

［2］Introduction Into HVDC PLUS，Siemens AG，Berlin，Germany 2008.https：／／www.energy－portal.siemens.com.

［3］管敏渊，徐政，屠卿瑞，等.模块化多电平换流器型直流输电的调制策略［J］.电力系统自动化，2010，34（2）：48－52.

［4］李强，贺之渊，汤广福，等.新型模块化多电平换流器空间矢量脉宽调制方法［J］.中国电机工程学报，2010，34（22）：74－79.

［5］丁冠军，汤广福，丁明，等.新型多电平电压源换流器模块的拓扑机制与调制策略［J］.中国电机工程学报，2009，29（36）：1－7.

［6］Bai Zhihong，Zhang Zhongchao，Zhang Yao.A Generalized Three－phase Multilevel Current Source Inverter with Carrier Phase－shifted SPWM［C］∥Power Electronics Specialists Conference，2007，1：2055－2060.

［7］Gemmell B，Dom J，Retzmann D，et al.Prospects of Multilevel VSC Technologies for Power Transmission［C］∥Proceedings of IEEE PES Transmission and Distribution Conference and Exposition，2008，1：1－16.

［8］Solas E，Abad G，Barrena J A，et al.Modulation of Modular Multilevel Converter for HVDC Application［C］∥Power Electronics and Motion Control Conference（EPE／PEMC），201014th International，2010，2：84－89.

［9］汤广福.基于电压源换流器的高压直流输电技术［M］.北京：中国电力出版社，2010.