永磁同步电机转子初始位置检测研究
杨立永,陈为奇
(北方工业大学 机电工程学院,北京 100144)
1 引言
近些年来,由于永磁材料的发展和新的控制算法的提出,高性能的永磁同步电机得到了广泛应用,目前永磁同步电机已经广泛应用于交流伺服系统中。在永磁同步电机传动控制系统中,电机转子初始定位与位置检测是构成完整系统的基本条件和正常运行的必要条件,也是按转子磁链定向矢量控制的必要条件。只有准确知道永磁同步电机的转子在任意时刻的确定位置,才可以通过坐标变换进行矢量控制,将永磁同步电机按照他励直流电机的控制方法进行控制,并可以达到他励直流电机传动系统的性能指标。
在未知转子初始位置情况下,直接启动永磁同步电机会出现所不期望的现象。对于转子初始位置的估算,许多研究者进行了大量的研究,提出了许多解决方案。有采用高频注入法来检测零速下的转子位置[1];有利用电机的磁饱和特性来检测转子初始位置[2]。但是这些方法主要依赖硬件电路和电机参数。本文通过对常用通直流电把转子拉到指定位置的实现研究,提出了利用增量式光电编码器的A,B脉冲信号,利用DSP的高速运算能力,在电机启动前确定转子初始位置的方法。
2 永磁同步电机工作原理
如图1所示,1个二极永磁转子,当定子三相绕组通上空间和时间上相差120°的三相交流电后,就产生1个旋转磁场,图1中用另一对旋转磁极来表示,该旋转磁场将以同步转速Ns旋转。由于磁极同性相斥,异性相吸的原理,那么旋转的磁场带着转子一起旋转,并以同步转速Ns旋转。当转子加上负载转矩之后,转子磁极轴线将落后定子磁场轴线1个角度,随着负载增加,这个角度也随之增大;负载减少时,此角度也减小;只要不超过一定限度,转子始终跟着定子的旋转磁场以恒定的同步转速Ns旋转。

图1 永磁同步电机工作原理Fig.1 Working principle of permanent magnet synchronous motor
3 未知转子初始位置启动分析
在未知转子的初始位置情况下,直接启动永磁同步电动机有可能出现所不期望的现象。
首先假设启动电机时,给定的电流矢量方向的初始角度与A轴的夹角为零。根据转子位置和三相ABC坐标系中A轴的夹角的关系可以分为以下4种情况。
1)转子与A轴夹角为0°,如图2所示。在这种情况下,转子在磁场力作用下的力臂最大,此时的对应力矩最大,即电机在启动过程中d轴与A轴的夹角为零。这就是所期望的永磁同步电机的正常启动情况。

图2 转子与A轴夹角为0°Fig.2 The rotor and Aaxis angle is 0°

图3 转子与A轴夹角为90°Fig.3 The rotor and Aaxis angle is 90°
2)转子与A轴夹角为90°,如图3所示。在这种情况下,转子在磁场作用下的力臂为零,所受的力矩为零,在此情况下启动,转子将静止不转,即电机无法启动,这是启动过程中所不期望的现象。
3)转子与A轴夹角为锐角,如图4所示。在这种情况下,转子受到的力矩不是最大,在空载的情况下,电机也许可以转动,但是电机没有足够大的转矩。这种情况电机不能带重载启动,或者启动过程中会产生过流现象。

图4 转子与A轴夹角为锐角Fig.4 The rotor and Aaxis angle is acute
4)转子与A轴夹角为钝角,如图5所示。这种情况下启动,由图5可知,由于同性相斥,异性相吸的原理,通电后产生的磁场会先排斥转子,即出现反转的现象,随后转过一定角度后又吸引转子,这样启动过程中会出现抖动的现象。这也是启动中不期望的现象。

图5 转子与A轴夹角为钝角Fig.5 The rotor and Aaxis angle is obtuse
在未知转子初始位置的情况下,启动永磁同步电机,以上4种情况是随机的出现,然而大多数情况是人们所不期望的启动现象,所以为了更好地控制永磁同步电机,应该确定转子的初始位置后再启动。
4 转子位置的检测方法
根据矢量id=0控制算法,空间矢量脉宽调制SVPWM以及矢量控制中的坐标变换方法,在永磁同步电机控制系统的双闭环控制中运用传统的PI控制,这样可以得到的系统模型如图6所示。

图6 id=0控制算法双闭环结构图Fig.6 Double loop chart for id=0control algorithm
4.1 通直流法
在未知转子初始位置的情况下,可以给定子通直流电,产生恒定的磁场,这样就可以把转子拉到指定的位置,此时就可以确定转子的初始位置,并在这种情况下对永磁同步电机进行矢量控制。具体的操作方法是:首先令id为一个较小常数,iq值为零,电流矢量角度值为零,这种情况产生的电流矢量的方向沿三相静止坐标系中的A轴。这就相当于在A轴方向产生一对磁极,如图7所示。根据磁极同性相斥,异性相吸的原理,就可以让转子转到已知的A轴位置。

图7 通直流电产生恒定磁场Fig.7 Produce a constant magnetic field through DC
本实验中给定的参数为:id=0.2,iq=0(标幺值),θ=0°。
已知逆PARK变换公式:

由式(1)、式(2)解得:

已知逆Clarke变换公式:

由式(3)、式(4)解得:

式中:iα,iβ分别是两相静止坐标下α轴和β轴的电流;id,iq分别是两相旋转坐标下d轴和q轴的电流;iA,iB,iC分别是三相静止坐标下A 轴、B 轴和C轴的电流。
由此可知三相ABC电流产生的电流矢量方向沿A轴方向,如图7所示。
结合永磁同步电机双闭环结构图,在转子初始定位过程中应该停止速度调节器工作,同时电流调节器输入给相应的定值产生一个恒定磁场。在这个磁场的作用下,转子会转动,使d轴与A轴重合,使转子转到已知的位置,在此情况下可以直接启动电机。通直流转子定位流程图见图8。

图8 通直流转子定位流程图Fig.8 Using DC find the rotor position flowchart
4.2 基于增量式编码器A,B信号搜索法
该方法的基本思想是在确定转子位置的过程中,保证转子位置几乎不动,而改变三相电所产生的电流矢量的方向,通过读取增量式光电编码器产生的A,B信号来获得转子微动的方向信息,再利用DSP的高速运算能力,不断地获取转子极微小的移动方向,进而来确定电机转子与A轴的夹角近似值。
实验中是以3对极永磁同步电机为例进行实验的,那么360°的机械空间被划分为3个部分,转子的位置范围可能是在0°到120°之间。假设转子位置在图9所示中的某一位置,下面通过搜索法来寻找转子与A轴的夹角。
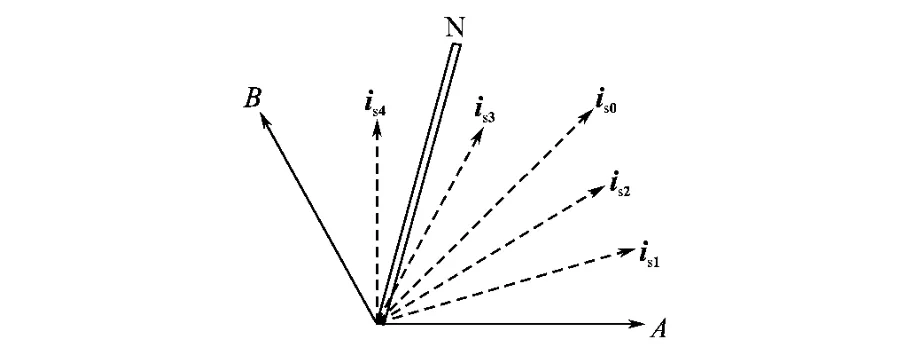
图9 搜索法原理示意图Fig.9 Schematic diagram of the search method
具体的操作方法是:上电后首先产生沿与A轴方向夹角为60°的电流矢量is0,通过分析增量式光电编码器A,B信号,进而确定电机微转动的方向,如果转子是顺时针微动,那么可以确定转子的范围在60°到120°之间;如果是逆时针微动,转子的位置在0°到60°之间。如果是第1种情况,那么就再产生1个与A轴夹角是90°方向的电流矢量is4,此时再判断转子的微动方向,如果是顺时针微动,转子位置在90°到120°之间,反之则在60°到90°之间。对于第2种情况,需要产生1个与A轴夹角为30°的电流矢量is1,如果转子顺时针微动,那么其就在30°到60°之间,反之就在0°到30°之间。下面的操作类推,总可以在1个很小的区间内使电机的转子处于微振状态。每次测试,区间减少二分之一。
在很多情况下,确定转子的初始位置是不允许电机转动的,所以转子一旦开始转动,控制系统通过检测到的增量式编码器的A,B脉冲信号反馈来判断转子的微动方向,然后系统按照上述方法不断修正转子与A轴的夹角,给电机特定方向的电流矢量。每次测试,其夹角均做相应修正,则经过多次试探后,系统对此夹角的修改将在极小范围内进行,电机转子处于微振动状态,转子的初始位置完成。
在确定转子的初始位置过程中,只要给电机施加的电流矢量is与电机转子的d轴不重合,那么电机肯定会旋转,这是无法避免的。但是,只要电机有微小的转动,光电编码器就会有A,B脉冲信号输出,通过DSP处理芯片读取转子微动的方向,再改变电机电流空间矢量的位置,在很短的时间内,如此反复进行测试,就可以不断地逼近电机转子的真实角度。在测试过程中,电机只能旋转几个脉冲对应的角度,而不会出现连续运行状态。同时又由于光电编码器每旋转一周所输出的脉冲达几千个,再经过倍频后就达到几万个,因此电机旋转输出几个脉冲它所产生的角位移是很小的,这在一般场合下是允许的。
转子初始位置的真实角度和估算角度的最大误差与测试次数的关系为

式中:Δθ为转子的实际角度和所估算角度差的最大误差;N为测试的次数。具体的关系见表1。

表1 角度误差最大值与测试次数关系表Tab.1 The chart for the relation of maximum angular error and times of tests
由式(5)和表1可知,实际角度和估算角度的最大误差随着检测的次数增加而减少。当检测的次数为8次的时候,最大误差值就为0.46875°,这在一定范围内是允许的。但是随着检测次数增多,程序的结构必然也随之复杂。
结合永磁同步电机双闭环结构图,在确定转子初始位置的过程中,首先应该停止速度调节器的工作,然后给适当的电流矢量幅值和不同的方向,该电流矢量维持适当的时间,以便能够读取转子微动的方向信息。搜索法程序流程图如图10所示。

图10 搜索法程序流程图Fig.10 Search method flowchart
这种方法中,电流矢量的幅值和作用时间是非常重要的参数,如果施加到电机上的电流矢量的幅值太大或者作用时间过长,则可能在检测过程中电机开始转动,因此实施转子初始位置检测之前,必须给定合适的电流矢量幅值和作用时间,使得转子初始位置检测能够正常运行。本文中给出的方法是:首先给定每一个电流矢量作用时间为t,然后把t分为n等分,当n从零开始逐渐增加,电流矢量的幅值从零逐渐增加,同时也不断地检测转子方向的输出信息,一旦方向值有变化,说明此时的电流矢量的幅值让转子转动了,然后记下转子转动的方向,再把电流矢量的幅值置为零,换下一个电流矢量,以下操作方法类似。即一旦检测到转子有微动,就立即使作用的电流矢量为零。这样可以保证转子不会出现大的转动,只是在原有的位置上微动。
5 实验分析
本实验是基于TI公司的TMS320F2812控制器实现的,永磁同步电机参数是3对极,1.1 kW,编码器码盘数为2500。
5.1 通直流转子定位实验
如图11所示,上面一条曲线是A相电流的波形,在前5s内,给定一个恒定直流电,转子会转到与A轴重合。图11中下面的曲线是电机角度输出曲线,会产生一个尖峰,说明转子在此电流作用下转动到指定位置,然后在此角度下开始启动电机。

图11 通直流转子定位实验波形Fig.11 Using DC find the rotor position experimental waveforms
5.2 搜索法转子定位实验
如图12所示,上面一条曲线是A相电流波形,每100ms改变一次电流矢量的方向,在图12中可以看出阶梯形的跳动,于此同时转子也随之而跳动,为了能看到转子随电流矢量方向的改变而改变,此时所通电流幅值不能固定,所以这种方法并不能满足在检测转子初始位置过程中保证转子不动。在此基础上需要逐渐增加电流矢量的幅值,如图13所示,上面的曲线是A相电流波形,可以看出在检测转子初始位置过程中,在给定方向下,电流矢量幅值逐渐增加。下面的波形是转子角度波形,定位过程中的角度是给定的,一旦确定角度后就从给定的角度开始启动。在检测到转子开始微动的时候,就立即把电流的幅值置为零,给定下一个电流矢量。

图12 搜索法转子定位波形图Fig.12 Search method for the rotor position experimental waveforms
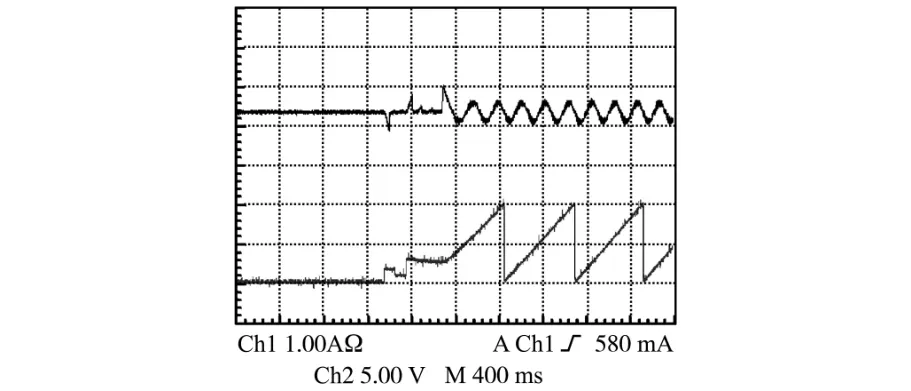
图13 改进搜索法的波形Fig.13 Improved searching method experimental waveforms
通直流的方法虽然简单,但是会使电机发热,其次对于有负载的启动行不通,同时在某些场合下电机启动前是不允许转动的。搜索法寻找转子初始位置的方法保证了搜索过程中转子没有转动,但是程序实现较为复杂,对所给定的电流矢量的幅值和作用时间有较高的要求。
6 结论
本文所提出的基于光电编码器A,B脉冲信号的搜索法,利用了DSP芯片的高速运算能力,快速的找到转子位置,可以很好地启动永磁同步电动机。
[1]贾洪平,贺益康.基于高频注入法的永磁同步电动机转子位置检测研究[J].中国电机工程学报,2007,27(15):15-20.
[2]丁荣军,黄济荣.现代交流技术与电气传动[M].北京:科学出版社,2009.
[3]陈荣,严仰光.永磁同步电机转子位置检测与定位[J].中小型电机,2003,30(3):61-65.
[4]陈荣.基于增量式光电编码盘的永磁同步电机转子位置初始定位[J].控制与应用技术,2007,34(3):32-34.
[5]程方斌,赵荣祥,蔡慧,等.一种新颖的永磁同步电动机启动策略的研究[J].电气传动,2005,35(9):10-12.
[6]Chung Dae-Woong,Kang Jun-Koo,Sul Seung-Li.Initial Rotor Position Detection of PMSM at Standstill Without Rotational Transducer[J].IEEE,1999:785-787.
[7]陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社,2003.

