基于改进电压模型的无轴承同步磁阻电机转子位移估计方法
张汉年,孙刚,刘合祥
(1.南京信息职业技术学院 电子信息学院,江苏 南京 210046;2.东南大学 电气工程学院,江苏 南京 210096)
1 引言
无轴承同步磁阻电机是一种高技术含量、高附加值的新型特种电机,该电机可产生固有旋转并能实现稳定悬浮。无轴承同步磁阻电机具有一系列突出的优点:低噪声、低功耗、高转速、免润滑、高洁净等,具有广泛的应用前景,在数控精密机床驱动、飞轮储能发电系统、家用电器、工业机器人控制等电力传动领域极具应用价值。与永磁型、感应型、开关磁阻型等其他类型的无轴承电机相比,无轴承同步磁阻电机具有控制简单、坚固可靠、转矩脉动低等优点[1]。
无轴承同步磁阻电机悬浮控制的关键环节是转子径向位移的精确检测,目前的方法大都是采用机械式电涡流位移传感器来获取转子径向位移[2]。但采用位移传感器带来的缺陷主要有:增大电机及其系统的复杂程度和体积,同时降低电机的可靠性;位移传感器增大系统的成本,而且对安装条件和使用环境要求严格,制约电机的推广应用。
基于电压模型的磁链观测方法在普通交流电机无速度传感器控制中获得成功应用[3],但该方法在电机低速时性能不佳,而无轴承电机一般应用于高速领域,因此该方法较适用于无轴承电机,目前已有学者将其应用于无轴承永磁同步电机的无位移传感器控制[4],但尚未发现该方法在无轴承同步磁阻电机中的应用。本文提出了基于改进电压模型的无轴承同步磁阻电机转子位移估计方法,仿真和实验结果证实了该方案的有效性。
2 电机转子径向位移估计基本原理
2.1 悬浮绕组磁链观测
悬浮绕组磁链估计直接影响无位移传感器控制系统的性能,本文采用改进电压模型的磁链估计方法,保证了磁链观测的准确性。
在两相静止坐标下,无轴承同步磁阻电机悬浮绕组的磁链估计模型为[5]
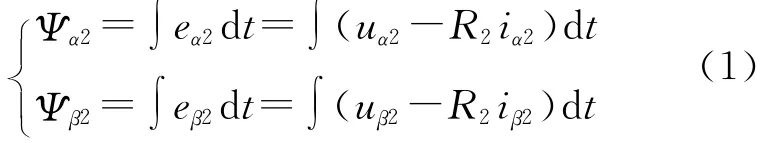
式中:eα2,eβ2为电机悬浮绕组的定子反电动势;uα2,uβ2为悬浮绕组等效电压;iα2,iβ2为悬浮绕组等效电流;R2为悬浮绕组电阻。
为降低式(1)中纯积分环节带来的积分初始化偏差,以及消除电压、电流检测所带来的直流偏置和漂移问题,采用输入信号截止频率为ωc的低通滤波器取代式(1)中纯积分环节,为弥补低通滤波器带来的相位滞后和幅值偏差,引入悬浮绕组的磁链参考值进行补偿,改进后的悬浮绕组磁链观测器数学模型为

式中:s为拉普拉斯算子。

图1 改进的电压模型结构图Fig.1 Block diagram of modified voltage model
图1中,首先将两相静止坐标下的悬浮绕组磁链值Ψα2,Ψβ2经直角/极坐标变换后,获得合成后的磁链幅值Ψs2和角度θ,其变换公式为

上述磁链幅值Ψs2再经限幅环节饱和限幅后,进行极坐标/直角坐标变换,从而获得悬浮绕组的磁链参考值。其中,磁链限幅值设定为磁链的参考值。
将两相静止坐标下悬浮绕组的磁链Ψα2,Ψβ2,转换为两相同步旋转d-q坐标下的磁链Ψx,Ψy为

基于上述改进电压模型的悬浮绕组磁链观测器的原理结构如图2所示。

图2 磁链观测器的原理结构图Fig.2 Principle diagram of the flux observer
2.2 转子径向位移的估计
无轴承同步磁阻电机是一种结构新颖的交流电机,转子结构与普通同步磁阻电机相同,其定子槽中嵌有极对数差值为1的两套绕组[6]:转矩绕组和悬浮绕组,通过控制这两套绕组中的电流不仅能使电机产生电磁转矩,同时能产生径向悬浮力。
在两相同步旋转d-q坐标下,无轴承同步磁阻电机转矩绕组和悬浮绕组的磁链方程为[7]

式中:Ψd,Ψq分别为转矩绕组d,q轴磁链;id,iq分别为转矩绕组d,q轴电流;ix,iy分别为悬浮绕组d,q轴电流;Ld,Lq分别为转矩绕组d,q轴电感;Lx,Ly分别为悬浮绕组d,q轴电感,因悬浮绕组按一定的规律对称排列,故Lx=Ly;x,y分别为转子在两轴方向的径向位移;Kd,Kq分别为电机d,q轴悬浮力/电流常数,其大小为[8]

式中:假定电机凸极转子极弧角度为30°;μ0为真空磁导率;l为电机铁心长度;r为转子外径;N2,N4分别为悬浮绕组和转矩绕组每相串联有效匝数;δ为气隙长度。
依据式(5),可得悬浮绕组磁链与悬浮绕组、转矩绕组中电流关系为

令Ψx-Lxix=ΔΨx,Ψy-Lyiy=ΔΨy,求解式(7),可得电机转子径向位移的表达式为

式(8)构建了电机转子位移估计器的数学模型,由式(8)可知,可以通过检测无轴承同步磁阻电机两套绕组自身的电流、电压信号,进而观测悬浮绕组的磁链值,最终估计出电机转子径向位移的大小。
将上述两相旋转坐标下的转子位移分量x,y转换成静止坐标下的分量α,β为
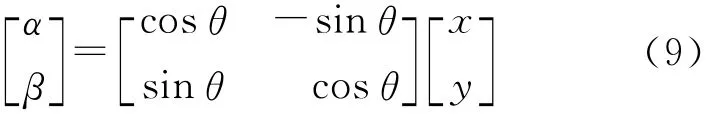
图3是包含坐标变换的转子径向位移估计结构图。

图3 转子位移估计结构图Fig.3 Block diagram of rotor displacements estimation
3 无位移传感器控制系统构成
无轴承同步磁阻电机完整的无位移传感器控制系统包含转矩控制子系统和悬浮控制子系统,转子悬浮控制的前提是建立悬浮力与电机两套绕组电流之间的关系。
在两相静止α-β坐标系下,电机悬浮绕组电流iα2,iβ2与径向悬浮力Fα,Fβ的关系为[9]

式(10)即为悬浮力/电流调制的数学模型,当悬浮力/电流调制模型的输入为径向悬浮力的参考值时,依据式(9)可得悬浮绕组的电流指令值
图4给出了包含转矩控制子系统、悬浮控制子系统、磁链估计和转子位移估计器的无位移传感器控制系统结构。图4中转子位移给定值和估计值的偏差经PD调节器后产生悬浮力参考值,再经悬浮力/电流调制输出两相参考电流将此电流与从悬浮绕组检测并经坐标变换得到的两相电流之间的偏差送入PI调节器,产生两相电压参考值,将其作为SPWM电压源逆变器的输入,该逆变器输出实际需要的三相电压向被控电机悬浮绕组供电,产生转子所需的径向悬浮力,从而实现转子的稳定悬浮运行。

图4 电机无位移传感器控制系统结构Fig.4 Block diagram of the displacements sensorless control system for the motor
图4中,无轴承同步磁阻电机的转矩控制子系统采用恒励磁电流矢量控制[10],该方法控制简单,不需要复杂的磁场定向。当固定励磁电流分量时,电磁转矩的大小同转矩电流分量成正比。
4 仿真与实验结果分析
4.1 仿真结果
为验证本方案无轴承同步磁阻电机转子位移估计方法的可行性,基于上述图4结构,在Matlab/Simulink环境下进行了控制系统仿真研究。电机参数为:转矩绕组极对数p1=2,转矩绕组d轴电感Ld=0.035H,q轴电感Lq=0.007H,转矩绕组每相电阻Rs1=0.25Ω;悬浮绕组极对数p2=1,悬浮绕组等效两相绕组的自感Lx=Ly=0.02H,悬浮绕组每相电阻Rs2=0.15Ω;转子质量m=1kg,转动惯量J=0.002kg·m2,气隙长度δ=0.3mm,额定转速n=3000r/min,额定转矩T=5N·m。
图5为电机空载启动且设定额定转速时,转子α轴方向实际位移和估计位移仿真结果。α轴初始位移为α=0.10mm,由仿真结果看出,系统能及时估计出转子位移,相比转子实际位移,转子估计位移的调节时间和超调量稍大,但估计位移能很快收敛于中心给定位置。
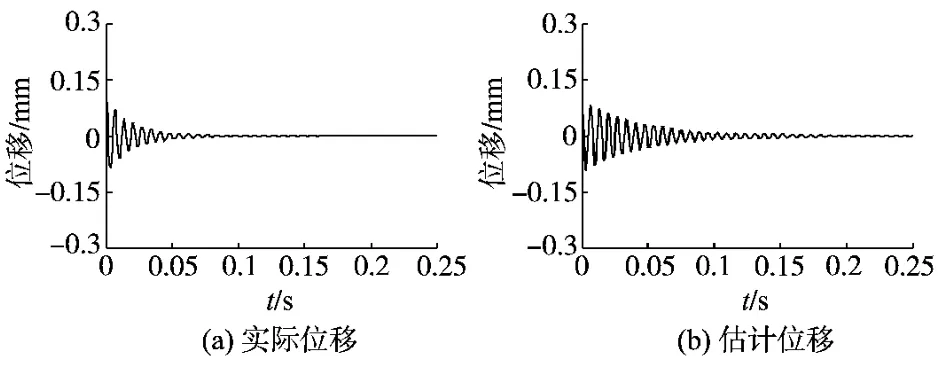
图5 α轴实际位移及估计位移Fig.5 α-axis real displacements and estimation displacements
图6为电机转矩和转速响应曲线,电机带3 N·m负载启动,并在0.1s突加5N·m负载转矩;转速初始设定为1000r/min,在0.1s转速突变为500r/min,由图6可见系统具有快速、良好的转矩与转速响应。

图6 电机转矩和转速响应Fig.6 The motor response of torque and of speed
图7为上述负载条件下α,β轴方向转子估计位移曲线,设定位移初始位置为α=0.10mm,β=-0.15mm。由图7看出,与空载相比,负载条件下α轴转子估计位移偏差增大,动态响应变慢,但位移振动的峰-峰值始终稳定在合理范围之内,转子最终趋于中心位置,两轴方向转子位移对转矩突变和转速调节具有良好的抗干扰性。由此可见,该位移估计方法可以确保电机在转速和转矩突变时均能实现稳定悬浮运行。
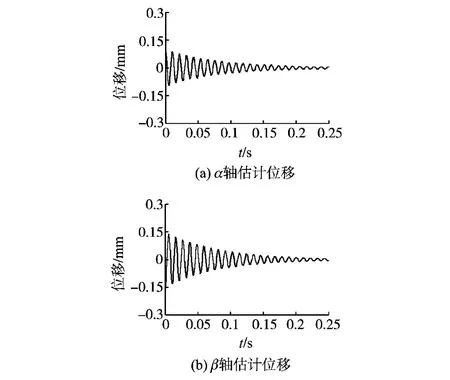
图7 α轴、β轴估计位移曲线Fig.7 α-axis,β-axis estimation displacements
4.2 实验结果
图8a为电机在额定转速和额定负载运行时,转子α轴方向上的估计位移曲线(无位移传感器)和实际位移曲线(有位移传感器)。其中转子估计位移曲线的跳动峰-峰值小于150μm,证实电机实现了稳定悬浮,但估计位移的脉动幅度比实际检测位移要大,这与仿真结果一致。
图8b为基于改进电压模型和传统电压模型进行悬浮绕组磁链观测时,转子β轴方向上的径向位移曲线。其中电机运行在额定转速和额定负载条件下,可以看出改进电压模型下的转子径向位移波动幅度比传统电压模型要小,说明改进电压模型对悬浮绕组磁链和转子位移的观测更加准确,进一步证实了本文所提方法的有效性。

图8 稳态运行时的实验结果Fig.8 The steady-state experiment results
5 结论
本文采用基于反电动势积分并结合改进电压模型的方法来观测电机悬浮绕组磁链,适用于高速运行中的无轴承同步磁阻电机,避免了传统电压模型所带来的积分初始化误差和积分漂移问题。基于上述磁链观测器的转子位移估计方法,能较好地实现对转子实际位移的跟踪,并且控制系统结构简单,易于实现。并对无轴承同步磁阻电机的无位移传感器控制系统进行了仿真和实验研究,结果表明,采用本方法的控制系统具有良好的动态和静态性能,电机转子能实现稳定悬浮运行,且具有较好的抗干扰能力。
[1]张汉年,刘合祥.两种不同转子结构的无轴承同步磁阻电机悬浮特性分析[J].微特电机,2011,39(2):15-18.
[2]Tera T,Yamauchi Y,Chiba A,et al.Perfomances of Bearingless and Sensorless Induction Motor Drive Based on Mutual Inductances and Rotor Displacements Estimation[J].IEEE Trans.on Industry Applications,2006,53(1):187-194.
[3]钟建强,游林儒,徐芹文.一种改进电压模型的异步电机无速度传感器矢量控制方法[J].微电机,2009,36(5):16-18.
[4]柏仓,黄守道,管晓文,等.无轴承永磁同步电机无位移传感器系统建模与仿真[J].电气传动,2009,39(9):60-63.
[5]周立求,朱建华,辜乘林.轴向叠片各向异性转子同步磁阻电机直接转矩控制的研究[J].中国电机工程学报,2006,26(4):154-158.
[6]Hertel L,Hofmann W.Magnetic Couplings in a Bearingless Reluctance Machine[C]∥Proc.of ICEM,2000:1776-1780.
[7]Michioka C,Sakamoto T,Ichikawa O,et al.A Decoupling Control Method of Reluctance-type Bearingless Motors Considersing Magnetic Saturation[J].IEEE Trans.on Industry Applications,1996,32(5):1204-1210.
[8]Zhang Hannian,Zhu Huangqiu,Zhang Zhibao,et al.Design and Simulation of Control System for Bearingless Synchronous Reluctance Motor[C]∥Proc.of ICEMS,2005(1):554-558.
[9]Hertel L,Hofmann W.Design and Test Results of a High Speed Bearingless Reluctance Motor[C]∥Proc.of 8th European Conference on Power Electronics and Applications,Lausanne,September,1999:1-7.
[10]Bimal K Bose.现代电力电子学与交流传动[M].北京:机械工业出版社,2006.

